Triongl hafalochrog
Gwedd
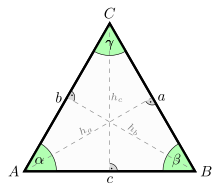
* ochrau'n hafal (a=b=c),
* yr onglau'n hafal (),
* yr uchderau'n hafal (ha=hb=hc).
Mewn geometreg, polygon rheolaidd yw'r triongl hafalochrog, sy'n driongl lle mae'r dair ochr yn gyfartal. O fewn geometreg Ewclidaidd, mae gan pob triongl hafalochrog ochrau cyfath, sy'n 60 ° yr un.
Prif nodweddion
[golygu | golygu cod]O ddynodi hyd yr ochrau yn a, yna fe ellir dweud, gan ddefnyddio Theorem Pythagoras fod:
- yr arwynebedd yn
- y perimedr yn
- radiws yr amgylch (circumscribed circle) yn
- radiws y mewngylch (inscribed circle) yn neu
- canol geometrig y triongl hefyd yn ganol i'r amgylch a'r mewnglych
- uchder (neu hyd) o bob ochr yn .
O ddynodi radiws yr amgylch yn R, yna fe eelir dweud, drwy ddefnyddio trigonometreg fod:
- yr arwynebedd yn [1]
Ceir perthynas syml rhwng yr llawer o'r meintiau hyn ag uchder ("h") pob fertig o'r ochr gyferbyn:
- Yr arwynebedd yw
- Uchder y canol o bob ochr (hy yr apothem), yw
- Radiws y cylch sy'n amgylchu'r 3 fertig yw
- Radiws y mewngylch yw
| Polygonau |
|
Triongl | Pedrochr | Pentagon | Hecsagon | Heptagon | Octagon | Nonagon | Decagon | Hendecagon | Dodecagon | Triskaidecagon | Tetradecagon | Pentadecagon | Hexadecagon | Heptadecagon | Octadecagon | Enneadecagon | Icosagon | Chiliagon | Myriagon |
Cyfeiriadau
[golygu | golygu cod]- ↑ Bencze, Mihály; Wu, Hui-Hua; Wu, Shan-He (2008). "An equivalent form of fundamental triangle inequality and its applications". Research Group in Mathematical Inequalities and Applications 11 (1). http://rgmia.org/papers/v11n1/equivalent.pdf.












