Բնական լոգարիթմ

Բնական լոգարիթմ, e հիմքով լոգարիթմ, որը իռացիոնալ հաստատուն է և հավասար է մոտ 2.72։ Այն նշանակվում է ${\displaystyle \ln x}$, ${\displaystyle \log _{e}x}$ կամ երբեմն ուղղակի ${\displaystyle \log x}$, երբ հիմքը ենթադրվում է ${\displaystyle e}$^[1]։ Սովորաբար լոգարիթմատակ արտահայտության ${\displaystyle x}$ արգումենտը իրական թիվ է, բայց այս հասկացությունը կարելի է ընդհանրացնել նաև կոմպլեքս թվերի համար։

Սահմանումից հետևում է, որ լոգարիթմական ֆունկցիան ${\displaystyle y=e^{x}}$ ցուցչային ֆունկցիայի հակադարձ ֆունկցիան է, ուստի նրանց գրաֆիկները համաչափ են առաջին և երրորդ քառորդների կիսորդի նկատմամբ։ Այն պատկանում է տրանսցենդենտ ֆունկցիաների դասին։

Բնական լոգարիթմները օգտակար են այն հանրահաշվական հավասարումների լուծման մեջ, որտեղ անհայտը ցուցիչում է։ Անփոխարինելի է մաթեմատիկական անալիզում, մաթեմատիկայի շատ բնագավառներում, կիրառական որոշ գիտություններում, ֆինանսական ոլորտի բազմաթիվ խնդիրներում (օրինակ բարդ տոկոսների հաշվման մեջ)։

x թվի բնական լոգարիթմ է կոչվում այն թիվը, որով պետք է աստիճան բարձրացնել e հիմքը՝ x ստանալու համար։ Այլ կերպ ասած․ բնական լոգարիթմը՝ ${\displaystyle \ln a}$ դա ${\displaystyle e^{x}=a}$ հավասարման ${\displaystyle x}$ լուծումն է։ Օրինակներ․

${\displaystyle \ln e=1}$, քանի որ ${\displaystyle e^{1}=e}$;

${\displaystyle \ln 1=0}$, քանի որ ${\displaystyle e^{0}=1}$։

${\displaystyle \ln a}$ բնական լոգարիթմը ${\displaystyle a}$ իրական թվի համար նույնպես սահմանվում է և ճիշտ է ցանկացած դրական ${\displaystyle a}$ թվի համար։

Բնական լոգարիթմը ցանկացած դրական իրական a թվի համար սահմանվում է նաև երկրաչափորեն՝ որպես ${\displaystyle y={\frac {1}{x}}}$ կորով սահմանափակված տիրույթի մակերես ${\displaystyle [1;a]}$ հատվածի վրա։

Լոգարիթմի սահմանումից էլ հենց ստացվում է հիմնական լոգարիթմական նույնությունը^[2]։

${\displaystyle e^{\ln a}=a}$

Կարևոր են նաև հետևյալ նույնությունները, որտեղ արժեքները համարվում են դրական․^[3]:

	Բանաձև	Օրինակ
Արտադրյալ	${\displaystyle \ln(xy)=\ln x+\ln y}$	${\displaystyle \ln(4\cdot 3)=\ln 4+\ln 3}$
Քանորդ	${\displaystyle \ln \left({\frac {x}{y}}\right)=\ln x-\ln y}$	${\displaystyle \ln \left({\frac {1}{e^{2}}}\right)=\ln(1)-\ln(e^{2})=0-2=-2}$
Աստիճան	${\displaystyle \ln(x^{p})=p\ln x}$	${\displaystyle \ln(64)=\ln(2^{6})=6\ln 2}$
Արմատ	${\displaystyle \ln {\sqrt[{p}]{x}}={\frac {\ln x}{p}}}$	${\displaystyle \ln {\sqrt {10}}={\frac {1}{2}}\ln 10}$

Այլ հատկություններ

• Արգումենտի աճի հետ աճում է նաև լոգարիթմը․ եթե ${\displaystyle 0<x<y,}$, ապա ${\displaystyle \ln x<\ln y}$;
• ${\displaystyle {\frac {h}{1+h}}\leqslant \ln(1+h)\leqslant h,}$, եթե ${\displaystyle h>-1}$։

Լոգարիթմը կարող է որոշված լինել ոչ միայն ${\displaystyle e}$ հիմքի, այլ ցանկացած դրական ${\displaystyle 1}$-ից տարբեր հիմքի համար։ ${\displaystyle a}$ հիմքով ${\displaystyle \log _{a}b}$ լոգարիթմը կարելի է ձևափոխել ^[4] բնական լոգարիթմի և հակառակը․

${\displaystyle \ln b={\frac {\log _{a}b}{\log _{a}e}}=\log _{a}b\cdot \ln a}$

${\displaystyle \log _{a}b={\frac {\ln b}{\ln a}}}$

Տասնորդական(${\displaystyle \lg x}$) լոգարիթմի և բնական լոգարիթմի կապը․ ^[5]

${\displaystyle \ln x\approx 2{,}30259\ \lg x;\quad \lg x\approx 0{,}43429\ \ln x}$

Երկուական (${\displaystyle \operatorname {lb} x}$) լոգարիթմի և բնական լոգարիթմի կապը․

${\displaystyle \ln x\approx 0,693147\operatorname {lb} x;\quad \operatorname {lb} x\approx 1{,}442695\ln x}$։

Եթե լոգարիթմվող թիվը ընդունենք որպես փոփոխական, ապա կստանանք ${\displaystyle y=\ln x}$ լոգարիթմական ֆունկցիան։ Այն որոշված է,երբ ${\displaystyle x>0}$։ Արժեքների տիրույթն է՝ ${\displaystyle E(y)=(-\infty ;+\infty )}$։ Այս կորը հաճախ անվանվում է լոգարիթմական^[6]։ Ֆունկցիան աճող է, անընդհատ ու դիֆերենցելի իրեն որոշման տիրույթում։ Աբցիսների առանցքը (${\displaystyle x=0}$) հանդիսանում է հորիզոնական ասիմպտոտ, քանի որ

${\displaystyle \lim _{x\to 0+0}\ln x=-\infty }$

Բնական լոգարիթմի ածանցյալը հավասար է․

${\displaystyle {\frac {d}{dx}}\ln x={\frac {1}{x}}}$։

Այս բանաձևի պարզության պատճառով է հենց լոգարիթմական ֆունկցիան կիրառվում մաթեմատիկական անալիզում և դիֆերենցիալ հավասարումներում։

Ինտեգրելով ածանցյալի բանաձևը ${\displaystyle x=1}$-ից մինչև ${\displaystyle x=b}$ միջակայքը, մենք կստանաք․

${\displaystyle \ln b=\int \limits _{1}^{b}{\frac {dx}{x}}}$

Այլ խոսքով․ բնական լոգարիթմը հավասար է ${\displaystyle y={\frac {1}{x}}}$ հիպերբոլով սահմանափակված մակերեսին x միջակայքի համար։

${\displaystyle y=1/x}$ ֆունկցիայի նախնականը ունի հետևյալ տեսքը․

${\displaystyle \int {dx \over x}=\ln |x|+C,}$

որտեղ ${\displaystyle C}$-ն ինտեգրման հաստատունն է։ Քանի որ ${\displaystyle y=1/x}$ ֆունկցիան կազմված է երկու ճյուղերից (մեկը դրական, մյուսը՝ բացասական ${\displaystyle x}$-երի համար), ապա ${\displaystyle y=1/x}$-ի նախնականների ընտանիքը նույնպես կազմված է երկու ենթաընտանիքներից, ընդ որում նրանց ինտեգրման հաստատունները անկախ են միմյանցից։ Բնական լոգարիթմից անորոշ ինտեգրալը հեշտ է գտնել մասերով ինտեգրմամբ։

${\displaystyle \int {\ln x\,\mathrm {d} x}=x\ln x-x+C}$

Մաթեմատիկական անալիզում և Դիֆերենցիալ հավասարումների տեսությունում մեծ դեր ունի ${\displaystyle f(x)}$ ֆունկցիայի լագարիթմական ածանցյալ հասկացությունը․

${\displaystyle {\frac {d}{dx}}\ln(f(x))={\frac {f'(x)}{f(x)}}}$։

Բնական լոգարիթմը վերլուծենք ըստ Թեյլորի շարքի․

${\displaystyle \ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+\dots }$

(շարք 1)

Այս շարքը, որը կոչվում է Մերկատորի շարք, զուգամիտում է, երբ ${\displaystyle -1<x\leqslant 1}$։ Մասնավորապես․

${\displaystyle \ln 2=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+\dots }$

Շարքը զուգամիտում է դանդաղ։ Նրանից կարելի է ստանալ առավել հարմար բանաձև․

${\displaystyle \ln \left({\frac {1+x}{1-x}}\right)=2\left(x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\dots \right)}$

(շարք 2)

Այս շարքը արդեն արագ է զուգամիտում։ Բացի այդ, բանաձևի ձախ մասով կարելի է արտահայտել ցանկացած դրական թվի լոգարիթմ։ Այս ալգորիթմով հնարավոր է հաշվել լոգարիթմների արժեքները, բայց այն դժվար է։ Շատ թվանշանների առկայության դեպքում Թեյլորի շարքով հաշվարկը էֆեկտիվ չէ։ Կիրառելի է որպես այլընտրանքային միջոց Նյուտոնի մեթոդը։ Դիտարկվում է հետևյալ բանաձևը․ ^[7][8]։

${\displaystyle \ln x\approx {\frac {\pi }{2M(1,4/s)}}-m\ln 2}$

որտեղ ${\displaystyle M}$ դա 1 և 4/s-ի թվաբանա-երկրաչափական միջինն է։

${\displaystyle s=x\,2^{m}>2^{p/2}}$։

Բերենք մի քանի օգտակար սահմանների օրինակներ լոգարիթմների համար ^[9]․

${\displaystyle \lim _{x\to 0}{\frac {\ln(1+x)}{x}}=1}$

${\displaystyle \lim _{x\to 0^{+}}x^{b}\ln x=0\quad (b>0)}$

${\displaystyle \lim _{x\to \infty }{\frac {\ln x}{x^{b}}}=0\quad (b>0)}$

${\displaystyle \ln x=\lim _{n\to \infty }n\left({\sqrt[{n}]{x}}-1\right)=\lim _{n\to \infty }n\left(1-{\frac {1}{\sqrt[{n}]{x}}}\right)}$

${\displaystyle \ln x=\lim _{h\to 0}{\frac {x^{h}-1}{h}}}$

Լոգարիթմի ներկայացման համար կիրառվում են մի քանի անընդհատ կոտորակներ․

${\displaystyle \ln(1+x)={\frac {x^{1}}{1}}-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+{\frac {x^{5}}{5}}-\dots ={\cfrac {x}{1-0x+{\cfrac {1^{2}x}{2-1x+{\cfrac {2^{2}x}{3-2x+{\cfrac {3^{2}x}{4-3x+{\cfrac {4^{2}x}{5-4x+\ddots }}}}}}}}}}}$

${\displaystyle \ln \left(1+{\frac {2x}{y}}\right)={\cfrac {2x}{y+{\cfrac {x}{1+{\cfrac {x}{3y+{\cfrac {2x}{1+{\cfrac {2x}{5y+{\cfrac {3x}{1+\ddots }}}}}}}}}}}}={\cfrac {2x}{y+x-{\cfrac {(1x)^{2}}{3(y+x)-{\cfrac {(2x)^{2}}{5(y+x)-{\cfrac {(3x)^{2}}{7(y+x)-\ddots }}}}}}}}}$

Բնական լոգարիթմի մասին առաջին տեղեկությունները հայտնվեցին 1619 թվականին, երբ լոնդոնցի մաթեմատիկայի ուսուցիչ Ջոն Սպենդելը վերահրատարակեց Նեպերի լոգարիթմական աղյուսակը՝ լրացնելով այն բնական լոգարիթմի աղյուսակներով^[10]։ 1649 թվականին բելգիացի մաթեմատիկոս Գրեգուար դը Սեն-Վենսանը ցույց տվեց, որ ${\displaystyle y={\frac {1}{x}}}$ հիպերբոլով սահմանափակված պատկերի մակերեսը փոխվում է լոգարիթմական օրենքով, և առաջարկեց դրանց անվանել «հիպերբոլական» լոգարիթմներ^[11]։ «Բնական լոգարիթմ» տերմինը առաջին անգամ օգտագործել է ��իկոլաս Մերկատորը իր «Logarithmotechnia» աշխատությունում, որը հրապարակվեց 1668 թվականին^[12]։ Այստեղ Մերկատորը ներկայացրեց լոգարիթմի վերլուծությունը Մերկատորի շարքով։ XVII—XVIII դարերում Գոթֆրիդ Լայբնիցը և Իոհան Բեռնուլլին բնական լոգարիթմը փորձեցին տարածել կոմպլեքս թվերի վրա, բայց ստեղծել ամբողջական տեսություն նրանց չհաջողվեց։ Բացասական և կոմպլեքս թվերի լոգարիթմների տեսությունը հրապարակվեց 1747-1751 թվականներին Էյլերի կողմից, և չի տարբերվում ժամանակակից տեսությունից^[13]։

Կոմպլեքս լոգարիթմը անալիտիկ ֆունկցիա է, որը ստացվում է իրական լոգարիթմը կոմպլեքս հարթության վրա տարածելով (բացի 0-ից)։ Կոմպլեքս լոգարիթմի ֆունկցիան բազմարժեք է։ Սահմանում Կոմպլեքս ${\displaystyle z}$ թվի ${\displaystyle \mathrm {Ln} \,z}$ բնական լոգարիթմը դա ${\displaystyle e^{w}=z.}$ հավասարման լուծումն է ${\displaystyle w}$^[6]։

${\displaystyle z}$ ոչ զրոյական թիվը կարելի է ներկայացնել ${\displaystyle z=r\cdot e^{i(\varphi +2\pi k)}\;\;,}$ բանաձևով, որտեղ ${\displaystyle k}$ —կամայակն ամբողջ թիվ է Ապա ${\displaystyle \mathrm {Ln} \,z}$ որոշվում է

${\displaystyle \mathrm {Ln} \,z=\ln r+i\left(\varphi +2\pi k\right)}$ բանաձևով։ Այստեղ ${\displaystyle \ln \,r=\ln \,|z|}$ իրական լոգարիթմն է^[14]։ Այսպիսով․

${\displaystyle \mathrm {Ln} \,z}$ կոմպլեքս լոգարիթմը գոյություն ունի ցանկացած ${\displaystyle z\neq 0}$ համար, և նրա իրական մասը որոշվում է միանշանակորեն, իսկ կեղծ մասը ունի անվերջ բազմությամբ լուծումներ՝ տարբերվելով միմյանցից ${\displaystyle 2\pi }$ արժեքով։

Բացասական թվի լոգարիթմը որոշվում է^[14]։

${\displaystyle \mathrm {Ln} (-x)=\ln x+i\pi (2k+1)\qquad (x>0,\ k=0,\pm 1,\pm 2\dots )}$ բանաձևով

Օրինակներ

${\displaystyle \ln(1)=0;\;\mathrm {Ln} (1)=2k\pi i}$

${\displaystyle \ln(-1)=i\pi ;\;\mathrm {Ln} (-1)=(2k+1)i\pi }$

${\displaystyle \ln(i)=i{\frac {\pi }{2}};\;\mathrm {Ln} (i)=i{\frac {4k+1}{2}}\pi }$

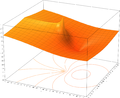
• Բնական լոգարիթմի ֆունկցիաները կոմպլեքս հարթության վրա(գլխավոր ճյուղ)
• 
  ${\displaystyle z=Re(\ln(x+iy))|}$
• 
  ${\displaystyle z=Im(\ln(x+iy))|}$
• 
  ${\displaystyle z=|\ln(x+iy)|}$
• 
  Երեք նախկին գրաֆիկների ընդհանրությունը

• Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
  • Переиздание: АСТ, 2003, ISBN 5-17-009554-6.
• Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
• Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с.
• Ա․Գ․Սվեշնիկով, Ա․Ն․Տիխոնով; Կոմպլեքս փոփոխականի ֆունկցիաների տեսություն, Մ․, Նաուկա,1966,էջ304։
• Գ․Մ․Ֆիխտենգոլց; Դիֆերենցիալ և ինտեգրալ հաշիվ,6-րդ հրատ․, — Մ.: Նաուկա, 1966. — էջ 680։

դ ք խ Մաթեմատիկայի ճյուղեր Հիմունքներ Կատեգորիաների տեսություն Ինֆորմացիայի տեսություն Մաթեմատիկական տրամաբանություն Մաթեմատիկայի փիլիսոփայություն Բազմությունների տեսություն Տիպերի տեսություն Հանրահաշիվ Աբստրակտ Կոմուտատիվ Տարրական Խմբերի տեսություն Գծային Բազմագծային Անալիզ Իրական անալիզ Կոմպլեքս անալիզ Դիֆերենցիալ հավասարումներ Ֆունկցիոնալ անալիզ Չափերի տեսություն Դիսկրետ Կոմբինատորիկա Գրաֆների տեսություն Կարգերի տեսություն Խաղերի տեսություն Երկրաչափություն Հանրահաշվական Անալիտիկ Դիֆերենցիալ Դիսկրետ Էվկլիդեսյան Վերջավոր Թվերի տեսություն Թվաբանություն Հանրահաշվական թվերի տեսություն Անալիտիկ թվերի տեսություն Դիոֆանտյան երկրաչափություն Տոպոլոգիա Հանրահաշվական Դիֆերենցիալ Երկրաչափական Կիրառական Կառավարման տեսություն Մաթեմատիկական տնտեսագիտություն Մաթեմատիկական ֆինանսներ Մաթեմատիկական ֆիզիկա Մաթեմատիկական վիճակագրություն Հավանականությունների տեսություն Վիճակագրություն Հաշվողական Ինֆորմատիկա Theory of computation Թվային մեթոդներ Օպտիմիզացիա Computer algebra Այլ Մաթեմատիկայի պատմություն Ժամանցային մաթեմատիկա Մաթեմատիկա և արվեստ Մաթեմատիկայի ուսուցում Կատեգորիա Վիքիպահեստ