Тетивно-тангентни четвороугао

Тетивно-тангентни четвороугао је четвороугао који је истовремено тетивни и тангентни.

Дефиниција оваквог четвороугла је

Четвороугао је тетивно-тангентан ако постоје кружница која садржи сва његова темена и кружница која додирује све његове странице.

Иако изгледа да је веома тешко конструисати уопштени случај оваквог четвороугла, важи следеће правило

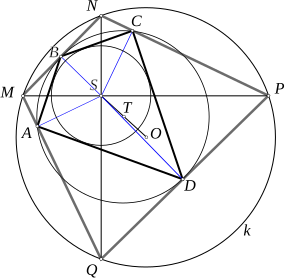
Нека је MNPQ тетивни четвороугао чије су дијагонале узајамно нормалне и секу се у тачки S. Ако су A, B, C и D нормалне пројекције тачке S на праве QM, MN, NP, PQ, редом, тада је четвороугао ABCD тетивно-тангентан^[1].

Сваки квадрат је тетивно-тангентни четвороугао.

Важи и да, уколико за дати пар кругова k₁ и k₂ постоји један тетивно-тангентни четовороугао ABCD који је уписан у круг k₁ и описан око круга k₂, тада за сваку тачку A' на кругу k₁ постоји тетивно-тангентни четвороугао ABCD уписан у круг k₁ и описан око круга k₂ (Штајнеров поризам).

Код оваквог четвороугла су занимљиве две особине које га разликују од других четвороуглова.

Нека је уписан круг са полупречником r и центром у тачки S, а описан круг полупречника R са сентром у тачки T и нека је О центар круга описаног око MNPQ. Тада

тачка ${\displaystyle T\,}$ полови дуж ${\displaystyle {\overline {OS}}}$.

Уколико означимо дужине страница тетивно-тангентног четвороугла са ${\displaystyle a\,}$, ${\displaystyle b\,}$, ${\displaystyle c\,}$ и ${\displaystyle d\,}$ тада се површина рачуна формулом

${\displaystyle P={\sqrt {abcd}}}$

• Тангентни четвороугао
• Тетивни четвороугао