പ്രോട്ടോൺ

ഇംഗ്ലീഷ് വിലാസം

https://ml.wikipedia.org/wiki/Proton

വിക്കിപീഡിയയുടെ ഗുണനിലവാരത്തിലും, മാനദണ്ഡത്തിലും എത്തിച്ചേരാൻ ഈ ലേഖനം വൃത്തിയാക്കി എടുക്കേണ്ടതുണ്ട്‌. ഈ ലേഖനത്തെക്കുറിച്ച് കൂടുതൽ വിശദീകരണങ്ങൾ നൽകാനാഗ്രഹിക്കുന്നെങ്കിൽ ദയവായി സംവാദം താൾ കാണുക. ലേഖനങ്ങളിൽ ഈ ഫലകം ചേർക്കുന്നവർ, ഈ താൾ വൃത്തിയാക്കാനുള്ള നിർദ്ദേശങ്ങൾ കൂടി ലേഖനത്തിന്റെ സംവാദത്താളിൽ പങ്കുവെക്കാൻ അഭ്യർത്ഥിക്കുന്നു.

Proton

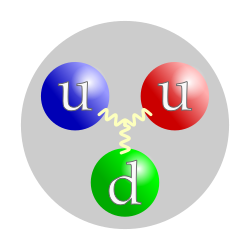പ്രോട്ടോണിന്റെ ക്വാർക്ക് ഘടന (The color assignment of individual quarks is not important, only that all three colors are present.)
വർഗ്ഗീകരണം	Baryon
ഘടകങ്ങൾ	2 up quarks, 1 down quark
മൗലിക കണത്തിൻ്റെ തരം	Fermionic
പ്രതിപ്രവർത്തനങ്ങൾ	Gravity, Electromagnetic, Weak, Strong
പ്രതീകം	Error no symbol defined, Error no symbol defined, Error no symbol defined
പ്രതികണം	Antiproton
സാന്നിധ്യം പ്രവചിച്ചത്	William Prout (1815)
കണ്ടെത്തിയത്	Ernest Rutherford (1919)
പിണ്ഡം	1.672621777(74)×10−27 കി.g[1] 938.272046(21) MeV/c2[1] 1.007276466812(90) u[1]
ശരാശരി ആയുസ്സ്	>2.1×1029 years (stable)
വൈദ്യുത ചാർജ്	+1 e 1.602176565(35)×10−19 C[1]
Charge radius	0.8775(51) fമീ[1]
Electric dipole moment	<5.4×10−24 e·cm
Electric polarizability	1.20(6)×10−3 fm3
കാന്തിക ആക്കം	1.410606743(33)×10−26 J·T−1[1] 1.521032210(12)×10−3 μB[1] 2.792847356(23) μN[1]
കാന്തിക ധ്രുവീയത	1.9(5)×10−4 fm3
ചക്രണം	1⁄2
Isospin	1⁄2
Parity	+1
Condensed	I(JP) = 1⁄2(1⁄2+)

ധന(+)ചാർജ്ജുള്ള ഒരു ഉപ ആണവകണമാണ്‌ പ്രോട്ടോൺ അഥവാ ധനകണം. p⁺ എന്ന ചിഹ്നമാണ് പ്രോട്ടോണിനെ സൂചിപ്പിക്കാൻ ഉപയോഗിക്കുന്നത് . ഓരോ അണുകേന്ദ്രത്തിലും ഒന്നോ‌ അതിൽ അധികമോ പ്രോട്ടോണുകൾ ന്യൂട്രോണുകൾക്കൊപ്പം ഉണ്ടാകും. ഒരു അണുകേന്ദ്രത്തിലെ പ്രോട്ടോണുകളുടെ എണ്ണത്തെയാണ് അണുസംഖ്യ എന്നു പറയുന്നത്. രാസപ്രവർത്തനങ്ങളിൽ ഈ കണങ്ങൾ പ്രധാന പങ്കുവഹിക്കുകയും വ്യത്യസ്ത മൂലകങ്ങളെ അതായി നിലനിർത്തുകയും ചെയ്യുന്നു.

കണികാ ഭൗതികത്തിന്റെ അടിസ്ഥാന മാതൃകയനുസരിച്ച് ക്വാർക്കുകൾ കൊണ്ട് നിർമ്മിതമായ ഒരു ഹാഡ്രോൺ ആണ് പ്രോട്ടോൺ. ഈ മാതൃകയെ ഭൗതിക ശാസ്ത്രജ്ഞർ സ്വീകരിക്കപ്പെടുന്നതിനു മുൻപ്, പ്രോട്ടോൺ ഒരു അടിസ്ഥാനകണമാണെന്ന് കണക്കാക്കപ്പെട്ടിരുന്നു. രണ്ട് അപ് ക്വാർക്കുകളും ഒരു ഡൗൺ ക്വാർക്കും അടങ്ങിയ പ്രോട്ടോണിന് 1.6–1.7 fമീ വ്യാസമുണ്ട്.^[2]

സ്വതന്ത്ര പ്രോട്ടോൺ സ്ഥിരതയുള്ള പദാർത്ഥമാണ്. അത് സ്വാഭാവികമായി വിവിധ ചുറ്റുപാടുകളിൽ കാണപ്പെടുന്നു. ഇലക്ട്രോണുകളുമായി യോജിക്കാൻ സാധിക്കാത്ത വിധം ഉയർന്ന താപനിലയായതിനാൽ പ്ലാസ്മയിൽ സ്വതന്ത്ര പ്രോട്ടോണുകൾ കാണാം. ശൂന്യതയിലൂടെ നക്ഷത്രാന്തര ദൂരങ്ങൾ താണ്ടുന്ന കോസ്മിക് വികിരണങ്ങളുടെ 90 ശതമാനവും ഉയർന്ന ഊർജ്ജവും പ്രവേഗവുമുള്ള സ്വതന്ത്രപ്രോട്ടോണുകളാണ്. അപൂർവ്വയിനത്തിൽപ്പെട്ട ചില റേഡിയോ ആക്റ്റീവ് ക്ഷയം മൂലം അണുകേന്ദ്രത്തിൽനിന്ന് സ്വതന്ത്രപ്രോട്ടോൺ നേരിട്ട് ഉത്സർജിക്കപ്പെടാം. അസ്ഥിരമായ സ്വതന്ത്രന്യൂട്രോണുകളുടെ ക്ഷയം മൂലവും ഇവയുണ്ടാകുന്നു. ഈ അവസരങ്ങളിലെല്ലാം ഇലക്ട്രോണുമായി കൂടിച്ചേരാൻ സാധ്യമല്ലാത്ത വിധം പ്രവേഗവും ഗതികോർജ്ജവും നഷ്ടമായാലേ അത് സ്വതന്ത്രപ്രോട്ടോണായി നിലനിൽക്കുകയുള്ളൂ. ഇലക്ട്രോണുകളുമായുള്ള അത്തരം ബന്ധനത്തിലും പ്രോട്ടോണിന്റെ സ്വഭാവത്തിൽ യാതൊരു മാറ്റവും വരുകയില്ല. അത് പ്രോട്ടോണായി തന്നെ നിലകൊള്ളുന്നു.

കുറഞ്ഞ ഊർജനിലയിലുള്ള പ്രോട്ടോണുകളും ഇലക്ട്രോണുകളും (സ്വതന്ത്ര ഇലക്ട്രോണുകളോ സാധാരണപദാർത്ഥങ്ങളിലുള്ള ഇലക്ട്രോണുകളോ) തമ്മിലുള്ള ആകർഷണം രാസബന്ധങ്ങളിലേക്ക് നയിക്കുന്നു. കുറഞ്ഞ താപനിലയിലാണ് (സൂര്യന്റെ ഉപരിതലതാപനിലയുമായി താരതമ്യപ്പെടുത്തുമ്പോൾ) ഇത് സംഭവിക്കുക. സാധാരണ (പ്ലാസ്മാരൂപത്തിലല്ലാത്ത) പദാർത്ഥങ്ങളുമായുള്ള പ്രതിപ്രവർത്തനത്തിൽ, കുറഞ്ഞ പ്രവേഗമുള്ള സ്വതന്ത്രപ്രോട്ടോണുകൾ ഏതെങ്കിലും അണുവിലേയോ തന്മാത്രയിലേയോ ഇലക്ട്രോണുകളിലേക്ക് ആകർഷിക്കപ്പെടുകയും അവ കൂടിച്ചേരുകയും ചെയ്യുന്നു. ശൂന്യതയിൽ, പര്യാപ്തമാം വിധം മന്ദമായ പ്രോട്ടോൺ ഒരു സ്വതന്ത്ര ഇലക്ട്രോണുമായി ചേർന്ന് നിഷ്ക്രിയമായ ഒരു ഹൈഡ്രജൻ അണുവായി മാറുന്നു.

പ്രധാന ലേഖനം: ക്വാർക്ക്

പ്രോട്ടോണിനെ വീണ്ടും വിഭജിച്ചാൽ ക്വാർക്കുകൾ ലഭിക്കുന്നു. ഇലക്ട്രോണുകളെ പോലെ ക്വാർക്കുകളും മൗലികകണികകളായാണ്‌ അറിയപ്പെടുന്നതെങ്കിലും വ്യത്യസ്ത ബലങ്ങൾ ഉൾക്കൊള്ളുന്ന അനവധി കണികാസംഘാതങ്ങൾ ഇവയിലും അടങ്ങിയിരിക്കുന്നുണ്ട്‌. ക്വാർക്കുകൾ ചാർജ്ജുള്ള കണികകളാണ് അപ്‌ ക്വാർക്കുകൾ +2/3 ചാർജും ഡൗൺ ക്വാർക്കുകൾ -1/3 ചാർജും വഹിക്കുന്നു. പ്രോട്ടോണുകളിൽ രണ്ട്‌ അപ്പ്‌ ക്വാർക്കുകളും ഒരു ഡൗൺ ക്വാർക്കുമാണുള്ളത്‌. അവയുടെ ആകെത്തുക +1 ആകുന്നു. ഇത്‌ 1.602 x 10 കൂളമ്പ്‌ എന്നു കിട്ടും. ഈ സംഖ്യ ഇലക്ട്രോണിലെ ഋണ ചാർജ്ജിനു തുല്യമായ ധനചാർജ്ജുകളാണ്. കൂടാതെ ഇത്‌ സ്ഥിരവുമാണ്‌. ഇലക്ട്രോണുകൾക്ക്‌ തുല്യമായത്രയും പ��രോട്ടോണുകളും ആറ്റത്തിലുണ്ടായിരിക്കും. എന്നാൽ പ്രോട്ടോണുകൾ ഇലക്ട്രോണുകളേക്കാൾ 1836 ഇരട്ടി വലിപ്പമുള്ളവയാണ്‌.

നാല്‌ അടിസ്ഥാനബലങ്ങളും പ്രോട്ടോണിനെ സ്വാധീനിക്കുന്നു. അവ ശക്തബലം, ക്ഷീണബലം, വിദ്യുത്‌കാന്തികബലം, ഗുരുത്വാകർഷണം എന്നിവയാണ്‌. ആറ്റത്തെ അതായി നില നിർത്താനും കാലക്രമേണ മറ്റൊന്നായി മാറാനും സഹായിക്കുന്നത്‌ ഈ ശക്തികൾ മാത്രമാണ്‌. വിദ്യുത്‌ കാന്തികബലം ഇലക്ട്രോണുകളെ ആറ്റത്തിന്റെ പരിധിയിൽ നിർത്തുമ്പോൾ ന്യൂക്ലിയർ അധിബലം പ്രോട്ടോണുകളേയും ന്യൂട്രോണുകളേയും പരസ്പരം യോജിപ്പിക്കുന്നു. അതിനാൽ തന്നെ ഇത്‌ കുറഞ്ഞദൂരത്തിൽ അതിശക്തമായ ആകർഷണ വികർഷണ സ്വഭാവം പ്രകടിപ്പിക്കുന്നവയാണ്‌. ഗുരുത്വാകർഷണം എന്നത്‌ പിണ്ഡത്തിനനുസരിച്ചു വർദ്ധിക്കും പ്രപഞ്ചത്തിലെവിടെയുമുള്ള മറ്റൊരു പിണ്ഡത്തെ അതു തന്നിലേക്കടുപ്പിക്കുന്നു. ആ അർത്ഥത്തിൽ പ്രപഞ്ചവും നമ്മളും തമ്മിൽ ബന്ധിപ്പിക്കുന്ന ശക്തിയുമാണിത്‌. എന്നാൽ പിണ്ഡം കുറയുമ്പോൾ ഇതിന്റെ വലിവു ബലം കുറയുന്നു. ഉദാഹരണത്തിന്‌ ഒരു മീറ്റർ ദൂരത്തിലുള്ള ഓരോ ടൺ പിണ്ഡങ്ങൾ തമ്മിൽ ഒരു പൗണ്ടിന്റെ 15 ദശലക്ഷത്തിലൊരംശം വലിവുബലം പ്രകടിപ്പിക്കുന്നു. ഈ ബലമാണ്‌ മഴത്തുള്ളികൾ ഭൂമിയിൽ പതിക്കുന്നതിനും നദി ഒഴുകുന്നതിനും നക്ഷത്രങ്ങളെ അതിന്റെ താരാപഥങ്ങളിൽ ചലിപ്പിക്കുന്നതിനും പ്രപഞ്ചത്തിന്റെ വികാസത്തെ ലഘൂകരിക്കുന്നതിനും ഉപകരിക്കുന്നതെന്ന വസ്തുത നമ്മെ അമ്പരപ്പിക്കും. ഗുരുത്വകർഷണത്തിന്‌ എതിരില്ലാത്തതിനാൽ അത്‌ ഇല്ലാതാവുന്നില്ല. ഇതാണ്‌ ഒരു മൂലകത്തെ മറ്റൊന്നായി മാറാൻ സഹായിക്കുന്നത്‌. ക്ഷീണബലം കണ്ടെത്തിയതിന്‌ പാകിസ്താനിലെ അബ്ദുൽസലാമിന്‌ നോബൽ സമ്മാനം ലഭിക്കുകയുണ്ടായി. പ്രോട്ടോണുകൾ മഹാവിസ്ഫോടനത്തിൽ ഒരു സെക്കന്റിന്റെ ആയിരത്തിലൊരംശം നേരം കൊണ്ട്‌ നിർമ്മിക്കപ്പെട്ടതായി കണക്കാക്കുന്നു. ഇതിന്റെ ജീവിതകാലം ഒന്നിനു ശേഷം 35 പൂജ്യമിട്ടാൽ കിട്ടുന്നത്രയും വർഷങ്ങളാണ്‌. എന്നാൽ പ്രപഞ്ചത്തിനാവട്ടെ 15ന്‌ പുറകെ 10 പൂജ്യമിട്ടാൽ കിട്ടുന്നത്ര പ്രായമേ ആയിട്ടുള്ളൂ. കാമ്പ്രിഡ്ജിലെ റൂഥർ ഫോർഡാണ്‌ ആദ്യമായി ഈ കണങ്ങളെ കണ്ടത്‌.

1918 ൽ ഏണസ്റ്റ് റൂഥർഫോർഡ് ആ‍ണ് പ്രോട്ടോണിനെ ആദ്യമായി തിരിച്ചറിഞ്ഞത്^{[അവലംബം ആവശ്യമാണ്]}.

ഭൗതികശാസ്ത്രവുമായി ബന്ധപ്പെട്ട ഈ ലേഖനം അപൂർണ്ണമാണ്‌. ഇതു വികസിപ്പിക്കുവാൻ സഹായിക്കുക. സഹായത്തിനു ഈ ലേഖനത്തിന്റെ ഇംഗ്ലീഷ് പതിപ്പ്.