Fonction polygamma

En mathématiques, la fonction polygamma d'ordre m est une fonction spéciale notée[1] ou et définie comme la m+1e dérivée du logarithme de la fonction gamma :
Ce qui équivaut à la dérivée me de la dérivée logarithmique de la fonction gamma :
- est la fonction digamma .
- La dérivée de la fonction gamma est donc
- .
- . On appelle parfois la fonction (ou ) la fonction trigamma.
- La dérivée seconde de la fonction gamma est donc
- .
Définition par une intégrale
[modifier | modifier le code]La fonction polygamma peut être représentée par :
Ceci n'est valable que pour Re (z) > 0 et m > 0. Pour m = 0, voir la définition de la fonction digamma.
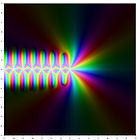
Représentation dans le plan complexe
[modifier | modifier le code] |
 |
 |
 |
 |
 |
| . | . | . | . | . | . |
Relation de récurrence
[modifier | modifier le code]Elle vérifie la relation de récurrence
Théorème de multiplication
[modifier | modifier le code]Le théorème de multiplication (en) donne
valable pour m > 1 ; et pour m = 0, la formule de multiplication de la fonction digamma est :
Représentation par série
[modifier | modifier le code]La fonction polygamma a pour représentation en série :
qui n'est valable que pour m > 0 et pour tout complexe z qui n'est pas égal à un nombre entier négatif. Cette représentation peut être écrite avec la fonction zêta de Hurwitz par
On peut en conclure que la fonction zêta de Hurwitz généralise la fonction polygamma à n'importe quel ordre appartenant à ℂ \ (–ℕ).
Série de Taylor
[modifier | modifier le code]La série de Taylor au point z = 1 est
qui converge pour |z| < 1. Ici, ζ est la fonction zêta de Riemann.
Notes et références
[modifier | modifier le code]- ↑ Polygamma Function sur mathworld.wolfram.com.
Références
[modifier | modifier le code]- (en) Milton Abramowitz et Irene Stegun, Handbook of Mathematical Functions, Dover Publications, 1964 (ISBN 978-0-486-61272-0), section 6.4
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Polygamma function » (voir la liste des auteurs).


























