From Wikipedia, the free encyclopedia
In mathematics , the polygamma function of order m is defined as the (m + 1)th
derivative of the logarithm of the gamma function :
ψ
(
m
)
(
z
)
=
(
d
d
z
)
m
ψ
(
z
)
=
(
d
d
z
)
m
+
1
ln
Γ
(
z
)
{\displaystyle \psi ^{(m)}(z)=\left({\frac {d}{dz}}\right)^{m}\psi (z)=\left({\frac {d}{dz}}\right)^{m+1}\ln \Gamma (z)}
Here
ψ
(
z
)
=
ψ
(
0
)
(
z
)
=
Γ
′
(
z
)
Γ
(
z
)
{\displaystyle \psi (z)=\psi ^{(0)}(z)={\frac {\Gamma '(z)}{\Gamma (z)}}}
is the digamma function and
Γ
(
z
)
{\displaystyle \Gamma (z)}
ψ
(
1
)
(
z
)
{\displaystyle \psi ^{(1)}(z)}
trigamma function .
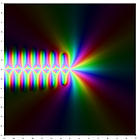
The logarithm of the gamma function and the first few polygamma functions in the complex plane
ln
Γ
(
z
)
{\displaystyle \ln \Gamma (z)}
ψ
(
0
)
(
z
)
{\displaystyle \psi ^{(0)}(z)}
ψ
(
1
)
(
z
)
{\displaystyle \psi ^{(1)}(z)}
ψ
(
2
)
(
z
)
{\displaystyle \psi ^{(2)}(z)}
ψ
(
3
)
(
z
)
{\displaystyle \psi ^{(3)}(z)}
ψ
(
4
)
(
z
)
{\displaystyle \psi ^{(4)}(z)}
Integral representation
The polygamma function may be represented as
ψ
(
m
)
(
z
)
=
(
−
1
)
(
m
+
1
)
∫
0
∞
t
m
e
−
z
t
1
−
e
−
t
d
t
{\displaystyle \psi ^{(m)}(z)=(-1)^{(m+1)}\int _{0}^{\infty }{\frac {t^{m}e^{-zt}}{1-e^{-t}}}dt}
which holds for Re z >0 and m > 0. For m = 0 see the digamma function definition.
Recurrence relation
It has the recurrence relation
ψ
(
m
)
(
z
+
1
)
=
ψ
(
m
)
(
z
)
+
(
−
1
)
m
m
!
z
−
(
m
+
1
)
.
{\displaystyle \psi ^{(m)}(z+1)=\psi ^{(m)}(z)+(-1)^{m}\;m!\;z^{-(m+1)}.}
Multiplication theorem
The multiplication theorem gives
k
m
ψ
(
m
−
1
)
(
k
z
)
=
∑
n
=
0
k
−
1
ψ
(
m
−
1
)
(
z
+
n
k
)
{\displaystyle k^{m}\psi ^{(m-1)}(kz)=\sum _{n=0}^{k-1}\psi ^{(m-1)}\left(z+{\frac {n}{k}}\right)}
for
m
>
1
{\displaystyle m>1}
m
=
0
{\displaystyle m=0}
digamma function :
k
(
ψ
(
k
z
)
−
log
(
k
)
)
=
∑
n
=
0
k
−
1
ψ
(
z
+
n
k
)
{\displaystyle k(\psi (kz)-\log(k))=\sum _{n=0}^{k-1}\psi \left(z+{\frac {n}{k}}\right)}
Series representation
The polygamma function has the series representation
ψ
(
m
)
(
z
)
=
(
−
1
)
m
+
1
m
!
∑
k
=
0
∞
1
(
z
+
k
)
m
+
1
{\displaystyle \psi ^{(m)}(z)=(-1)^{m+1}\;m!\;\sum _{k=0}^{\infty }{\frac {1}{(z+k)^{m+1}}}}
which holds for m > 0 and any complex z not equal to a negative integer. This representation can be written more compactly in terms of the Hurwitz zeta function as
ψ
(
m
)
(
z
)
=
(
−
1
)
m
+
1
m
!
ζ
(
m
+
1
,
z
)
.
{\displaystyle \psi ^{(m)}(z)=(-1)^{m+1}\;m!\;\zeta (m+1,z).}
Alternately, the Hurwitz zeta can be understood to generalize the polygamma to arbitrary, non-integer order.
The Taylor series at z = 1 is
ψ
(
m
)
(
z
+
1
)
=
∑
k
=
0
∞
(
−
1
)
m
+
k
+
1
(
m
+
k
)
!
ζ
(
m
+
k
+
1
)
z
k
k
!
,
{\displaystyle \psi ^{(m)}(z+1)=\sum _{k=0}^{\infty }(-1)^{m+k+1}(m+k)!\;\zeta (m+k+1)\;{\frac {z^{k}}{k!}},}
which converges for |z | < 1. Here, ζ is the Riemann zeta function . This series is easily derived from the corresponding Taylor's series for the Hurwitz zeta function. This series may be used to derive a number of rational zeta series .
References