Arquitas

Arquitas de Tarento (en griego antiguo: Ἀρχύτας ὁ Ταραντίνος; c. 430 a. C.- c. 360 a. C.) fue un filósofo, matemático, astrónomo, estadista, general y contemporáneo de Platón.

Arquitas trabajó en su ciudad natal, la colonia griega Tarento en Apulia. Como filósofo, perteneció a los pitagóricos. Se le conoce sobre todo por su relación amistosa con Platón, por la paloma voladora que se dice que inventó y por un experimento mental con el que intentó demostrar la infinitud del universo. Sólo se conservan algunos Fragmentos de sus escritos, que trataban en particular temas de matemáticas y música.

Como teórico de la ciencia, Arquitas era optimista. Creía que el conocimiento científico era fácil de obtener si se tenía el método adecuado. Hizo especial hincapié en las matemáticas como ciencia básica. Su logro matemático más significativo fue la solución del problema de duplicar el cubo. Esto demuestra que tenía una complejidad metodológica extraordinaria para su época. Contribuyó a la armónica musical con su teoría matemática del intervalo armónico. En óptica intentó encontrar una explicación para la reflexión y en Acústica para los diferentes tonos. Sus logros científicos, de los que poco se sabe debido a la escasez de datos conservados, fueron reconocidos por la posteridad antigua y por los historiadores modernos de la ciencia.

Arquitas desempeñó un papel político y militar decisivo como principal estadista y estratega de su ciudad natal y de una federación de colonias griegas en el sur de Italia liderada por ella. Sus éxitos militares le valieron una gran autoridad. En el ámbito interno, abogó por el equilibrio social, creyendo posible justificar científicamente un concepto de justicia y lograr así el consenso.

Arquitas nació en Tarento (Magna Grecia, hoy Italia) entre los años 435 y 410 a. C.^[1]​ Hijo de Hestieo, según Aristógenes, o de Mneságoras, según Diógenes Laercio. Fue comandante en tres guerras, y strategos de Tarento durante siete años (indicativo de su prestigio social) ya que la ley prohibía la reelección más de un año. Condujo una reforma política en Tarento mediante la que llegó a ser la ciudad más rica y poblada de la Magna Grecia. A través de la construcción de memoriales, templos y otros edificios le dio lustre a la ciudad. Ayudó a dar nuevos impulsos al comercio al buscar asociaciones con Istria, Grecia y África.

Arquitas de Tarento perteneció a la escuela secta de los Pitagóricos, alumno de la escuela de Filolao. Fue amigo de Platón, al que conoció durante el primer viaje que éste realizó al sur de Italia y a Sicilia en 388/387 a. C., tras la muerte de Sócrates. En su Carta Séptima, Platón asegura que Arquitas trató de rescatarlo en sus dificultades con Dionisio II de Siracusa, mediante una carta de recomendación y enviando un barco a Sicilia en 361 a. C.. Para algunos autores fue el maestro pitagórico de Platón y para otros su discípulo.^[1]​

Enseñó matemáticas a Eudoxo de Cnidos,^[2]​ siendo a su vez maestro de Menecmo. Fue la primera persona en lograr una buena aproximación al problema de la Duplicación del cubo,^[1]​ y uno de los primeros que, tras Pitágoras, trabajó en el conocimiento conjunto de la Aritmética, Geometría, Astronomía y Música, el Quadrivium, así como de la Acústica, acotando las matemáticas a disciplinas técnicas, con las cuales se cree haya inventado la polea, el tornillo y una especie de mecanismo articulado con alas, similar a un pájaro, al que logró hacer volar cerca de 300 metros gracias al impulso de un núcleo de vapor comprimido. Según Aristóteles fue el inventor del sonajero.^[3]​ Otros también aseguran su influencia directa sobre Euclides.

Según cuenta Horacio en una de sus odas, Arquitas falleció en un naufragio en las costas de Apulia entre los años 360 y 350 a. C.^[1]​ Horacio escribió que su cuerpo permaneció sin sepultura en la orilla hasta que un navegante le echó arena encima, pues de otra forma habría vagado en este lado del Lago Estige durante cien años.

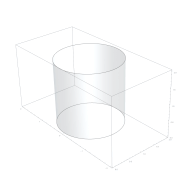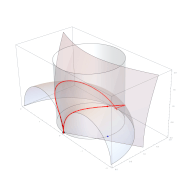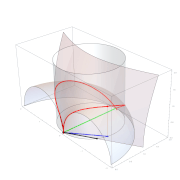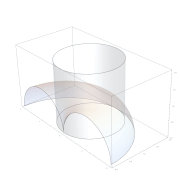
La curva de Arquitas es un caso particular de la curva de intersección de un toro y un cilindro. Se puede utilizar para duplicar el cubo.^[4]​^[5]​

• 
  Curva de Arquitas.
• 
  Curva de Arquitas.
• 
  Curva de Arquitas. Duplicación del cubo.

De las obras de Arquitas sólo han sobrevivido cuatro fragmentos ciertamente auténticos. No se encuentra ninguna lista de obras en las fuentes más antiguas. En épocas posteriores, muchas obras espurias circularon bajo su nombre.^[6]​ No se conocen los títulos originales de las obras auténticas, y la información proporcionada por los autores antiguos que las citan se considera poco fiable. La única certeza es que se trataban la música y las matemáticas. Para uno de los escritos, el título Sobre las ciencias se da en diferentes variantes (Perí mathematikón, Perí mathemáton, Peri mathematikés). Otra -o posiblemente parte de Sobre las ciencias- puede haberse titulado Armónicos. Otra obra, supuestamente titulada Tratados (diatribaí), posiblemente incluía un intento de dar una base científica a la ética. Archytas también pudo haber compuesto escritos sobre cosmología, biología, maquinaria y agricultura.^[7]​

Aunque Arquitas fue un contemporáneo más joven de Sócrates, a quien sobrevivió durante décadas, se le cuenta entre los Presocráticos porque pertenecía a una tradición más antigua que aún no estaba bajo la influencia de la filosofía socrática. Esta clasificación es problemática, sin embargo, porque sus obras fueron escritas después de la muerte de Sócrates.^[8]​

Arquitas consideraba la ciencia de los números, a la que llamaba logistikē, como el fundamento de las ciencias y también destacaba su primacía sobre la geometría. En su gran estima por las matemáticas, coincidía con Platón. Sin embargo, mientras Platón veía en el estudio de las matemáticas sólo una preparación para el estudio de la filosofía y su concepción de la educación apuntaba a una comprensión puramente intelectual de la realidad, Arquitas no compartía el desdén de Platón por el empirismo y tampoco hacía la tajante distinción platónica entre los ámbitos de lo intelectualmente conocible y lo sensiblemente perceptible. Para él, la aritmética también era importante desde el punto de vista político, porque parecía ofrecerle la posibilidad de encontrar fórmulas plausibles para una distribución consensuada y equilibrada de la propiedad entre los ciudadanos. Puesto que la aplicación de tales fórmulas era verificable para todos, podía, según la convicción de Arquitas, establecer y preservar la paz social. Esto era de suma importancia en las ciudades griegas, a menudo sacudidas por sangrientas luchas de poder. El equilibrio entre las clases sociales, que debía evitar conflictos violentos (stáseis en la ciudadanía, era una preocupación central de Arquitas. Él esperaba la realización del "cálculo" correcto y apropiado (logismós), que demostrablemente aseguraba que nadie se extralimitara.^[9]​

Bruno Snell señala el cambio de significado de la palabra máthema, que según su significado básico denota lo que se aprende o se puede aprender. Como designación de la ciencia, esta expresión aparece atestiguada por primera vez en Arquitas. Para el filósofo tarentino, las matemáticas eran el campo central del conocimiento, pero además de la geometría y la aritmética, la astronomía y la música también pertenecían a los mathémata. Arquitas llamaba a estas cuatro ciencias sistered. Sólo más tarde se redujo el campo de significado a las matemáticas, porque sólo las matemáticas parecían ser una ciencia en sentido propio, ya que sólo ellas parecían cumplir el requisito de que los objetos de una ciencia deben ser conocibles con total certeza.^[10]​

Al parecer, Arquitas desarrolló una filosofía de la ciencia como doctrina en la que trataba el arte de la búsqueda adecuada -el enfoque científico- como requisito básico para el éxito.^[11]​ Profesaba una erkenntnistheoretische optimista; según su creencia, los descubrimientos son fáciles y sencillos si se tiene el método adecuado.^[12]​ Los detalles de su método son difíciles de averiguar debido al estado desfavorable de las fuentes. Lo que ha sobrevivido es su principio de que primero hay que hacer buenas distinciones con respecto a la naturaleza del "todo"; una vez logrado esto, se puede comprender bien la naturaleza de los objetos individuales. En consecuencia, el conocimiento científico progresa de lo más general a lo más específico. A partir de la escasa información de las fuentes, no queda claro a qué se refería exactamente con los "enteros", como los conceptos generales de una ciencia en particular.^[13]​ En cualquier caso, Arquitas estaba convencido de que descubrir hechos por uno mismo era superior a adoptar lo que ya se sabía. Lo que uno mismo descubría era algo propio (ídion); el conjunto de conocimientos que uno adquiría aprendiendo era algo ajeno.^[14]​

En ética, Arquitas hacía especial hincapié en la exigencia de actuar siempre de acuerdo con la razón y nunca actuar espontáneamente por ira o dejar que los deseos nublaran la mente.^[15]​.

La tradición de que Arquitas fue también astrónomo se remonta a los poetas romanos Horacio y Propercio, que probablemente no disponían de información fidedigna al respecto. Auténtico y famoso, sin embargo, es su argumento a favor de la infinitud del universo. Se trata de un experimento mental que dice: Si alguien que hubiera llegado a un supuesto extremo del universo extendiera allí su mano o una vara, tendría que encontrarse o con un cuerpo o con el espacio vacío, es decir, en cualquier caso con una continuación del universo. Así pues, el cosmos debe extenderse infinitamente. Esta idea fue retomada y modificada por la Estoicos y el Epicúreos y aún por John Locke e Isaac Newton.^[16]​

Arquitas se ocupaba de las razones ${\displaystyle (n+1):n}$, que en la expresión de la época se llamaban "superproporcionales". Se trata de relaciones ${\displaystyle a:b}$ en las que el "exceso" de ${\displaystyle a}$ sobre ${\displaystyle b}$ es la enésima parte de ${\displaystyle b}$ y entonces ${\displaystyle a:b=(n+1):n}$ se cumple.^[17]​ Archytas encontró una prueba del teorema "Entre dos números en una relación superproporcional, nunca se pueden encontrar proporcionales medios (Media geométrica)." Esto significa, en terminología moderna, que hay irracional cocientes de magnitudes que no pueden representarse como cocientes de números racionales (número fraccionarios). La raíz cuadrada ${\displaystyle {\sqrt {(n+1):n}}}$ son irracionales.^[18]​.

Hipócrates de Quíos había conseguido reducir el problema de duplicar el cubo a un problema de razón: Bastaba con encontrar -es decir, construir geométricamente- para la distancia ${\displaystyle a}$, arista del cubo a doblar, las distancias ${\displaystyle u}$ y ${\displaystyle v}$ de tal manera que estuvieran en la razón ${\displaystyle a:u=u:v=v:2a}$. Entonces, a saber

${\displaystyle \left({\frac {a}{u}}\right)^{3}={\frac {a}{u}}\times {\frac {u}{v}}\times {\frac {v}{2a}}={\frac {a}{2a}}={\frac {1}{2}}.}$

Por tanto, se tiene ${\displaystyle 2\times a^{3}=u^{3}}$ y el cubo con arista ${\displaystyle u}$ es, como se deseaba, una duplicación del cubo con arista ${\displaystyle a}$.

Sin embargo, Hipócrates no consiguió construir ${\displaystyle u}$ y ${\displaystyle v}$ para distancias dadas ${\displaystyle a}$ y ${\displaystyle b}$ de tal manera que ${\displaystyle a:u=u:v=v:b}$ se cumpla, ni siquiera para el caso especial ${\displaystyle b=2a}$ que sólo se necesita aquí. Esto es lo que se esforzaron por hacer los eruditos antiguos posteriores. El matemático antiguo Eutocio, en su comentario al tratado Peri sphaíras kai kylíndrou (Sobre la esfera y el cilindro)' de Arquímedes, transmitió doce soluciones. La primera y mejor de ellas es la de Arquitas. Lo consiguió con la ayuda de la curva que lleva su nombre. Se trata de la primera curva -es decir, no contenida en ningún plano- utilizada en la historia de las matemáticas. La construcción utilizada para hallar una intersección de tres superficies curvas es única en la matemática antigua y resulta especialmente sorprendente para esta etapa temprana de la historia de las matemáticas. Sin embargo, en la investigación contemporánea se asume de forma abrumadora que en realidad se originó con Archytas.^[19]​

Para la solución Arquitas utilizó las superficies de tres sólidos: un toro, un cilindro y un cono. En la representación moderna usando coordenadas cartesianas convenientemente elegidas, estas superficies vienen dadas cada una de ellas por una de las siguientes ecuaciones:

${\displaystyle {\begin{matrix}x^{2}+y^{2}+z^{2}=a{\sqrt {x^{2}+y^{2}}}\\x^{2}+y^{2}=ax\\x^{2}+y^{2}+z^{2}={\frac {a^{2}}{b^{2}}}x^{2}\end{matrix}}}$

El toroide y el cilindro se intersecan en la curva de la arquieta. La intersección ${\displaystyle P}$ de esta curva con el cono es un punto que satisface las tres ecuaciones. Por tanto, se le aplica lo siguiente, si se abrevia.

${\displaystyle u={\sqrt {x^{2}+y^{2}+z^{2}}}}$  y  ${\displaystyle v={\sqrt {x^{2}+y^{2}}}}$

se escribe:

${\displaystyle \left\{{\begin{matrix}u^{2}=av\\v^{2}=ax\\u^{2}={\frac {a^{2}}{b^{2}}}x^{2}\end{matrix}}\right.}$

La primera ecuación dice ${\displaystyle a:u=u:v}$. Si el equivalente ${\displaystyle v^{2}}$ según la segunda ecuación se utiliza en la tercera ecuación para ${\displaystyle ax}$, el resultado después de la extracción de la raíz y la conversión es ${\displaystyle u:v=v:b}$. Así que en conjunto se cumple la relación deseada ${\displaystyle a:u=u:v=v:b}$. La distancia de ${\displaystyle P}$ al origen de coordenadas tiene longitud ${\displaystyle u}$; así se introdujo ${\displaystyle u}$. Es por tanto, en el caso ${\displaystyle b=2a}$, la arista del cubo doblado. Una reconstrucción del procedimiento de Archytas es dada por Stephen Menn.^[20]​ La construcción no tiene éxito si sólo se pueden utilizar compases y reglas; sin embargo, este requisito sólo se impuso en las matemáticas griegas después de Arquitas.

• El cráter lunar Archytas lleva este nombre en su memoria.^[21]​
• El asteroide (14995) Archytas también conmemora su nombre.^[22]​

• Diógenes Laercio: Vidas, opiniones y sentencias de los filósofos más ilustres; VIII, 79 - 83: Arquitas.
  • Texto español en la Biblioteca Virtual Miguel de Cervantes.
    • Texto griego en Wikisource.
• Arquitas: fragmentos y testimonios, con traducción y prólogo de Claudio R. Varela.
  • Texto bilingüe español - griego; documento de Word, en Internet Archive, que requiere el tipo de letra Palatino Lynotype. Versión oficial de la traducción en Hybris. Revista de Filosofía. CENALTES, Vol 3, N.º 2, 2012. pp 76- 100. (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última). ISSN 0718-8382 Texto español - griego.
• Fragmentos de la obra de Arquitas.
  • Texto francés, con comentarios en ese idioma, en el sitio de Philippe Remacle (1944 - 2011); trad. de Antelme Édouard Chaignet (1819 - 1901). 10.ª ed. París, 1874.
• Hermann Alexander Diels: Fragmentos de los presocráticos (Die Fragmente der Vorsokratiker). La primera edición se hizo en 1903 en Berlín, y fue dirigida por el propio Diels. A partir de la 5.ª, sustituiría a Diels Walther Kranz.
  • 35: Archytas.
    • Texto griego, con comentarios en alemán: 1.ª ed., de 1903, en facsímil electrónico en Internet Archive.
    • Textos de la 2.ª ed., de 1906, la mayoría en griego, alguno en latín y alguno en francés, en el sitio de Philippe Remacle.
• FARAH CALDERÓN, Walter: Entre la mentira y la verdad pitagórica: el caso de Arquitas de Tarento.
  • Texto en PDF, mediante registro, en Hybris, revista de filosofía. CENALTES, Vol.3- N.º 2. Otoño 2012. pp 46–74 ISSN 0718-8382.