Τρίγωνο του Ήρωνα

Στη γεωμετρία, το τρίγωνο του Ήρωνα είναι ένα τρίγωνο που έχει μήκη πλευρών και εμβαδόν, ακέραιους αριθμούς.^[1][2] Τα τρίγωνα του Ήρωνα πήραν το όνομά τους από τον Ήρωνα της Αλεξάνδριας. Ο όρος συχνά εφαρμόζεται ευρύτερα και σε τρίγωνα που οι πλευρές τους και το εμβαδόν τους είναι ρητοί αριθμοί.^[3]

Κάθε ορθογώνιο τρίγωνο με μήκη πλευρών που αντιστοιχούν σε Πυθαγόρεια τριάδα είναι τρίγωνο του Ήρωνα, καθώς τα μήκη των πλευρών κάθε τέτοιου τριγώνου είναι ακέραιοι αριθμοί, όπως και το εμβαδόν τους, το οποίο είναι το μισό του γινομένου των κάθετων πλευρών όπου τουλάχιστον μια πλευρά έχει μήκος άρτιο αριθμό.

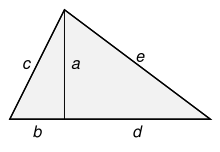
Παράδειγμα τρίγωνου του Ήρωνα που δεν είναι ορθογώνιο, αποτελεί το ισοσκελές τρίγωνο με μήκη πλευρών 5, 5, και 6, του οποίου το εμβαδόν είναι 12. Αυτό το τρίγωνο προκύπτει ενώνοντας δυο ορθογώνια τρίγωνα με πλευρές 3, 4, και 5, στην πλευρά με μήκος 4. Αυτός ο τρόπος προσέγγισης μπορεί να γενικευτεί, όπως φαίνεται και στην εικόνα δεξιά. Παίρνοντας Πυθαγόρεια τριάδα (a, b, c), με c το μεγαλύτερο και ακόμα μια (a, d, e), με e το μεγαλύτερο, μπορούμε να κατασκευάσουμε τρίγωνα με αυτά τα μήκη πλευρών και να τα ενώσουμε στην πλευρά a, ώστε να πάρουμε τρίγωνο με ακέραια μήκη c, e, και b + d, και με εμβαδόν

${\displaystyle A={\frac {1}{2}}(b+d)a}$ (το μισό της βάσης επί το ύψος).

Αν το a είναι άρτιος αριθμός τότε το εμβαδόν A είναι ακέραιος. Αν και δεν είναι προφανές, αν το a είναι περιττός, το A εξακολουθεί να είναι ακέραιος, αφού το b και d πρέπει να είναι και τα δυο άρτια, οπότε και το άθροισμα b+d είναι άρτιο επίσης.

Μερικά τρίγωνα του Ήρωνα δεν μπορούν να κατασκευαστούν ενώνοντας δυο ορθογώνια τρίγωνα με ακέραιες πλευρές, όπως παραπάνω. Για παράδειγμα αυτό με πλευρές 5, 29, 30 είναι τρίγωνο του Ήρωνα με εμβαδόν 72, αλλά δεν μπορεί να παραχθεί με δυο πυθαγόρειες τριάδες, μιας και κανένα ύψος του δεν είναι ακέραιος αριθμός. Επίσης κανένα πρωτογενές Πυθαγόρειο τρίγωνο δεν μπορεί να κατασκευαστεί από δύο μικρότερα ακέραια Πυθαγόρεια τρίγωνα.^[4]:p.17 Αυτά τα τρίγωνα του Ήρωνα είναι γνωστά και ως μη κατασκευάσιμα (indecomposable).^[4] Ωστόσο, αν κανείς δεχθεί Πυθαγόρειες τριάδες με γενικά ρητούς αριθμούς, και όχι απαραίτητα ακέραιους, τότε η αποσύνθεση σε ορθογώνια τρίγωνα με ρητές πλευρές μπορεί να γίνει πάντα,^[5] μιας και όλα τα ύψη ενός τριγώνου του Ήρωνα είναι ακέραιος (αφού είναι διπλάσιο του ακέραιου εμβαδού διαιρεμένο με την ακέραια βάση). Έτσι ένα τρίγωνο του Ήρωνα με πλευρές 5, 29, 30 μπορούν να κατασκευαστεί από ρητή Πυθαγόρεια τριάδα με πλευρές 7/5, 24/5, 5 και 143/5, 24/5, 29.

Κάθε τρίγωνο του Ήρωνα έχει πλευρές ανάλογες με του παρακάτω τύπους:^[6]

${\displaystyle a=n(m^{2}+k^{2})\,}$

${\displaystyle b=m(n^{2}+k^{2})\,}$

${\displaystyle c=(m+n)(mn-k^{2})\,}$

Ημιπερίμετρος${\displaystyle =s=(a+b+c)/2=mn(m+n)\,}$

Εμβαδόν${\displaystyle =mnk(m+n)(mn-k^{2})\,}$

Ακτίνα του εγγεγραμένου κύκλου${\displaystyle =k(mn-k^{2})\,}$

${\displaystyle s-a=n(mn-k^{2})\,}$

${\displaystyle s-b=m(mn-k^{2})\,}$

${\displaystyle s-c=(m+n)k^{2}\,}$

για ακέραια m, n και k με:

ΜΚΔ(m,n,k)=1

${\displaystyle mn>k^{2}\geq m^{2}n/(2m+n)\,}$

${\displaystyle m\geq n\geq 1\,}$.

Ο συντελεστής αναλογίας είναι γενικά ο ρητός ${\displaystyle {\frac {p}{q}}}$ με τον q=ΜΚΔ(a,b,c) να υποβιβάζει το παραγόμενο τρίγωνο του Ήρωνα στο πρωτογενές του και το ${\displaystyle p}$ να ανάγει το πρωτογενές στο απαιτούμενο μέγεθος. Για παράδειγμα, αν m = 36, n = 4 καιk = 3 τότε παράγεται τρίγωνο με a = 5220, b = 900 and c = 5400, που είναι όμοιο με το τρίγωνο του Ήρωνα 5, 29, 30 και με συντελεστή αναλογίας p = 1 και q = 180.

Λίστα με τα πρωτογενή ακέραια τρίγωνα του Ήρωνα. "Πρωτογενής" σημαίνει ότι ο μέγιστος κοινός διαιρέτης των τριών πλευρών είναι το 1.

• Τύπος του Ήρωνα
• Πυθαγόρεια τριάδα