Verse: Hyperdimension Neptunia
Hello~
This blog is to calculate the lifting strength of Blanc when she fight with her hammers.
| “ | Stop... Hammer Time! | „ |
| ~ MC Hammer |
The Hammers[]
"Steel Hammer: A supersized hammer made from steel." Official translation from Hyperdimension Neptunia.
"Hammer: A massive sledgehammer made of industrial steel." Official translation from Hyperdimension Neptunia Re;birth2 SISTERS GENERATION, Hyperdimension Neptunia Re;birth3: V Generation and Hyperdimension Neptunia Victory.
Calculations[]
Before I start with the calc I want to point out that, if in the images there is some parts of the hammers that I left out or the figure is bigger and takes more that it should, is because the position of the camara in the game, it should be good if it's in the right position.
Now let's go.
| “ | Then let's get to WUUUUURK! | „ |
| ~ Doctor Ivo "Eggman" Robotnik. |
- Steel Hammer
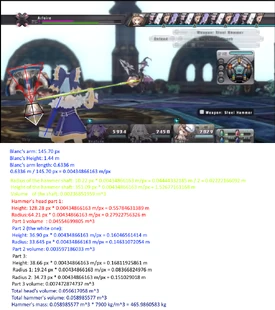
As you can see in the picture, most of the calc is there. Although I thought that this hammer was the hardest to calculate, in the end it was the easy one. I decided to split it in fourth parts: one cylinder, one conical frustum and two cones.
Blanc official height is 1.44 m, her arm is 44% of that. I used that value to do the pixel scaling.
- 1.44 m * 44 = 63.36 / 100 = 0.6336 m
The equation for volume of a cylinder is V= π * r^2 * h
V = π * (0.02222166092 m)^2 * 1.52677161168 m = 0.00236851959 m^3
The equation for volume of a cone is: V = 1/3 * π * r^2 * h
V = 1/3 * π * (0.27922756326 m)^2 * 0.55784631389 m = 0.04554699805 m^3
V = 1/3 * π * (0.14631072054 m)^2 * 0.16046561414 m = 0.003597186033 m^3
The equation for volume of a conical frustum is: V = 1/3 * π * h * (R^2 + (R * r) + r^2)
V = 1/3 * π * 0.16811925861 m * ((0.151029018 m)^2 + (0.151029018 m * 0.08366824976 m) + (0.08366824976 m)^2) = 0.007472874737 m^3
Total volume of the hammer is:
V = 0.00236851959 m^3 + 0.04554699805 m^3 + 0.003597186033 m^3 + 0.007472874737 m^3 = 0.058985577 m^3
The density of steel is between 7750 kg/m^3 and 8050 kg/m^3, so I used 7900 kg/m^3.
M = V * D
M = 0.058985577 m^3 * 7900 kg/m^3 = 465.9860583 kg
Baseline Class 1.
- Hammer
This one was more tricky because of the shaft, so I decided to not calc it since it will require take more pictures and, sadly, I don't own any of those games to do so. I think that three conical frustum are fine for the head. I used Blanc's arm again for the pixel scaling.
V = 1/3 * π * 0.105311362 m * ((0.284555095 m)^2 + (0.284555095 m * 0.163286216 m) + (0.163286216 m)^2) = 0.016994195 m^3
V = 1/3 * π * 0.666999453 m * ((0.284555095 m)^2 + (0.284555095 m * 0.231816946 m) + (0.231816946 m)^2) = 0.140167786 m^3
V = 1/3 * π * 0.049480671 m * ((0.231816946 m)^2 + (0.231816946 m * 0.172357672 m) + (0.172357672 m)^2) = 0.006394186724 m^3
Total volume of the hammer's head is:
V = 0.016994195 m^3 + 0.140167786 m^3 + 0.006394186724 m^3 = 0.16355616772 m^3
M = 0.16355616772 m^3 * 7900 kg/m^3 = 1292.093725 kg
Baseline Class 5.
Results[]
Steel Hammer = 465.9860583 kg or Class 1.
Hammer = 1292.093725 kg or Class 5
Keep in mind that the complete mass of both hammers should be higher because I didn't include some parts of them in the calcs.