Історія теорії ймовірності

Історія науки
Хронологія Давні часи Античність Давня Греція Середньовіччя Ісламське Середньовіччя Відродження Романтизм НТР
Культури Африканська Візантійська Індійська Ісламська Китайська Середньовічна Українська
Математика Алгебра Геометрія Обчислення Комбінаторика Логіка Статистика Теорія ймовірності Тригонометрія
Природничі науки Астрономія Біологія Біологічна еволюція Ботаніка Географія Геологія Геофізика Екологія Кліматологія Палеонтологія Фізика Хімія
Суспільні науки Антропологія Економіка Енвайронменталізм Історія Лінгвістика Політологія Психологія Соціологія Філософія
Технологія Обчислювальна техніка Інженерія Матеріалознавство Сільське господарство
Медицина Анатомія Ветеринарія Неврологія Нутриціологія Патологія Фармакологія
Інше Історіографія Псевдонаука Соціальний аспект
Хронологія • Категорія • Портал
п о р

Історія теорії ймовірності відзначена багатьма унікальними особливостями. Передусім, на відміну від інших розділів математики, які виникли приблизно в тому ж проміжку часу, (наприклад, математичного аналізу або аналітичної геометрії), у теорії ймовірностей по суті не було античних або середньовічних попередників, вона цілком — здобуток Нового часу^[1]. Довгий час теорія ймовірностей вважалася суто дослідною наукою і «не зовсім математикою»^[2][3], її строге обґрунтування було розроблено тільки в 1929 році, тобто навіть пізніше, ніж аксіоматика теорії множин (1922). У наші дні теорія ймовірностей займає одне з перших місць у прикладних науках за широтою своєї області застосування; «Немає майже жодної природничої науки, в якій так чи інакше не застосовувалися б ймовірнісні методи»^[4].

Історики виділяють у розвитку теорії ймовірностей кілька періодів^[5][6].

1. Передісторія, до XVI століття включно. В античні часи і в Середньовіччя натурфілософи обмежувалися метафізичними міркуваннями про походження випадковості і її значення у природі^[7]. Математики в цей період розглядали й іноді розв'язували завдання, пов'язані з теорією ймовірностей, але ніяких загальних методів і тематичних понять ще не з'явилося. Головним досягненням цього періоду можна вважати розвиток комбінаторних методів, які пізніше стали в пригоді творцям теорії ймовірностей.
2. Початок формування в другій половині XVII століття основних понять і методів теорії ймовірностей для випадкових величин зі скінченною кількістю значень. Стимулом спочатку слугували переважно проблеми, що виникали в азартних іграх, проте область застосування теорії ймовірностей майже відразу починає розширюватися, включаючи в себе прикладні завдання демографічної статистики, страхової справи і теорії наближених обчислень. На цьому етапі важливий внесок в ідеї нової науки внесли Паскаль і Ферма. Християн Гюйгенс ввів два фундаментальних поняття: числова міра ймовірності події, а також поняття математичного сподівання випадкової величини.
3. У XVIII столітті з'явилися монографії із систематичним викладом теорії ймовірностей. Першою з них стала книга Якоба Бернуллі «Мистецтво припущень» (1713 рік). У ній Бернуллі запропонував класичне означення ймовірності випадкової події як відношення кількості рівно можливих випадків, пов'язаних із цією подією, до загальної кількості випадків. Він також виклав правила підрахунку ймовірності для складних подій і дав перший варіа��т ключового «закону великих чисел», який пояснює, чому частота події в серії випробувань не змінюється хаотично, а в певному сенсі прагне до свого граничного теоретичного значенням (тобто ймовірності).
4. Ідеї ​​Бернуллі розвинули на початку XIX століття Лаплас, Гаусс та Пуассон. Застосування імовірнісних методів у прикладній статистиці значно розширилося. Поняття ймовірності було розвинуте для неперервних випадкових величин, завдяки чому з'явилася можливість застосування методів математичного аналізу. З'являються перші спроби застосування теорії ймовірностей у фізиці. До кінця XIX століття з'являються статистична фізика, сувора теорія помилок вимірювання, ймовірнісні методи проникають у різноманітні прикладні науки.
5. У XX столітті в фізиці була створена теорія мікросвіту, а в біології — теорія спадковості, обидві вони більшою мірою ґрунтуються на імовірнісних методах. Карл Пірсон розробив алгоритми математичної статистики, які широко застосовуються для аналізу прикладних вимірювань, перевірки гіпотез і прийняття рішень. А. М. Колмогоров дав класичну аксіоматику теорії ймовірностей. З інших нових сфер застосувань теорії ймовірностей необхідно згадати теорію інформації і теорію випадкових процесів. Філософські суперечки про те, що таке ймовірність і в чому причина її стійкості, тривають.

Ймовірне (англ. probable), очікуване (англ. likely) та інші тотожні назви походять з латинської probabilis та verisimilis, були запропоновані Цицероном та означають «правдоподібний», або «цілком схвалений».

У стародавньому та середньовічному Законі про Докази було розроблено класифікацію ступенів доведення, ймовірностей, презумпцій та напівдоказів, для того щоб можна було подолати неоднозначні ситуації в судах. В добу Відродження ставки були обговорені з точки зору шансів таких як «десять до одного», також у страхуванні морських суден виплати оцінювались на основі інтуїтивних ризиків, але не було ніякої теорії, яка б дозволяла точно рахувати такі премії чи ставки. Математичні методи у ймовірності з'явились у П'єра де Ферма та Блеза Паскаля (1657) в таких питаннях як справедливий розподіл частки в азартних іграх з перервами. Християн Гюйгенс (1657) дав комплексне трактування цього об'єкта.

Перші завдання імовірнісного характеру виникли в різних азартних іграх — кістках, картах та ін. Французький канонік XIII століття Рішар де Фурніваль^[en] правильно підрахував всі можливі суми очок після підкидування трьох кісток і вказав кількість способів, якими може вийти кожна з цих сум. Цю кількість способів можна розглядати як першу кількісну міру очікуваності події, аналогічну ймовірності. До Фурніваля, а іноді і після нього, цей захід часто підраховували невірно, вважаючи, наприклад, що суми 3 і 4 очка рівноімовірні, так як обидва можуть вийти «тільки одним способом»: за результатами підкидування «три одиниці» і «двійка з двома одиницями» відповідно. Водночас не враховувалося, що три одиниці справді виходять тільки одним способом: ${\displaystyle 1+1+1}$, а двійка з двома одиницями — трьома: ${\displaystyle 1+1+2;\;1+2+1;\;2+1+1}$, так що ці події не рівноімовірні. Аналогічні помилки неодноразово траплялися і в подальшій історії науки.

У великій математичної енциклопедії «Сума арифметики, геометрії, відносин і пропорцій» італійця Луки Пачолі (1494) містяться оригінальні завдання на тему: як розділити ставку між двома гравцями, якщо серія ігор перервана достроково. Приклад такого завдання: гра йде до 60 очок, переможець отримує всю ставку в 22 дуката, в ході гри перший гравець набрав 50 очок, другий — 30, і тут гру довелося припинити; потрібно справедливо розділити вихідну ставку. Рішення залежить від того, що розуміти під «справедливим» розділом; сам Пачолі запропонував ділити пропорційно набраним очкам (55/4 і 33/4 дуката); пізніше його рішення було визнано помилковим.

Великий алгебраїст XVI століття Джироламо Кардано присвятив аналізу гри змістовну монографію «Книга про гру в кості» (1526 рік, опублікована посмертно). Кардано провів повний і безпомилковий комбінаторний аналіз для значень суми очок і вказав для різних подій очікуване значення частки «сприятливих» подій: наприклад, під час підкидання трьох кісток частка випадків, коли значення всіх 3 кісток збігаються, дорівнює 6/216 або 1/36. Кардано зробив проникливе зауваження: реальна кількість досліджуваних подій може при невеликому числі ігор сильно відрізнятися від теоретичного, але чим більше ігор в серії, тим частка цієї відмінності менше. По суті, Кардано близько підійшов до поняття ймовірності:

Отже, є одне загальне правило для розрахунку: необхідно врахувати загальну кількість можливих випадінь і кількість способів, якими можуть з'явитися дані випадання, а потім знайти відношення останнього числа до числа залишившихся можливих випадінь.

Інший італійський алгебраїст, Нікколо Тарталья, розкритикував підхід Пачолі до вирішення завдання про розподіл ставки: адже якщо один із гравців ще не встиг набрати жодного очка, то алгоритм Пачолі віддає всю ставку його супернику, що важко назвати справедливим, оскільки деякі шанси на виграш у відстаючого все ж є. Кардано і Тарталья запропонували свої (різні) способи розділу, але згодом і ці способи були визнані невдалими.

Дослідженням даної теми займався і Галілео Галілей, який написав трактат «Про вихід очок при грі в кості» (1718 рік, опублікований посмертно). Виклад теорії гри у Галілея відрізняється вичерпною повнотою і ясністю. У своїй головній книзі Діалог про дві найголовніші системи світу, птоломєєвої і коперникової» Галілей також вказав на можливість оцінки похибки астрономічних та інших вимірів, причому заявив, що малі помилки вимірювання найімовірніше, ніж великі, відхилення в обидві сторони різноімовірні, а середній результат повинен бути близький до істинного значення вимірюваної величини. Ці якісні міркування стали першим в історії пророкуванням нормального розподілу помилок.

У XVII столітті почало формуватися чітке уявлення про проблематику теорії ймовірностей і з'явилися перші математичні (комбінаторні) методи вирішення імовірнісних задач. Засновниками математичної теорії ймовірностей стали Блез Паскаль і П'єр Ферма.

Перед цим математик-аматор шевальє де Мере звернувся до Паскаля щодо так званого «завдання про очки»: скільки разів потрібно підкинути дві кістки, щоб ставити на одночасне випадання хоча б раз двох шісток було вигідно? Паскаль і Ферма вступили в листування між собою щодо даного завдання і споріднених питань (1654). В рамках цього листування вчені обговорили низку проблем, пов'язаних з ймовірними розрахунками; зокрема, розглядалася стара задача про розподіл ставки, і обидва вчених прийшли до рішення, що треба розділити ставку відповідно шансам, що залишаються на виграш. Паскаль вказав де Мері на помилку, допущену ним під час вирішення «завдання про окуляри»: в той час як де Мері невірно визначив рівноімовірні події, отримавши відповідь: 24 підкидування, Паскаль дав правильну відповідь: 25 підкидувань.

Паскаль в своїх працях далеко просунув застосування комбінаторних методів, які систематизував у своїй книзі «Трактат про арифметичний трикутник» (1665). Спираючись на імовірнісний підхід, Паскаль навіть доводив (у посмертно опублікованих нотатках), що бути віруючим вигідніше, ніж атеїстом (див. «Парі Паскаля»).

Тематика дискусії Паскаля і Ферма (без подробиць) стала відома Християнові Гюйгенсу, який опублікував власне дослідження «Про розрахунки в азартних іграх» (1657): перший трактат з теорії ймовірностей. У передмові Гюйгенс пише:

Я вважаю, що при уважному вивченні предмета читач помітить, що має справу не тільки з грою, але що тут закладаються основи дуже цікавої і глибокої теорії.

У трактаті Гюйгенса детально викладаються питання, розглянуті Ферма і Паскалем, але ставляться і нові питання. Головним досягненням нідерландського вченого стало введення поняття математичного очікування, тобто теоретичного середнього значення випадкової величини. Гюйгенс також вказав класичний спосіб його підрахунку:

Якщо кількість випадків, в яких виходить сума a, дорівнює p, а кількість випадків, в яких виходить сума b, дорівнює q, то вартість мого очікування дорівнює ${\displaystyle {ap+bq \over p+q}}$.

Гюйгенс, як видно з цитати, спочатку використовував термін «вартість», а термін «очікування» з'явився вперше при перекладі трактату Гюйгенса Ван Схоутеном на латинську мову і став загальноприйнятим у науці.

У книзі є велика кількість завдань, деякі з рішеннями, інші «для самостійного вирішення». З останніх особливий інтерес і жваве обговорення викликала «задача про розорення гравця». У дещо узагальненому вигляді вона формулюється так: у гравців A і B є a і b монет відповідно, в кожній грі виграється одна монета, ймовірність виграшу A в кожній грі дорівнює p, потрібно знайти ймовірність повного його розорення. Повне загальне рішення «задачі про розорення» дав Абрахам де Муавр півстоліття пізніше (1711). У наші дні імовірнісна схема «задача про розорення» використовується при вирішенні багатьох завдань типу «випадкове блукання».

Гюйгенс проаналізував і завдання про розподіл ставки, давши його остаточне рішення: ставку треба розділити пропорційно можливостям виграшу при продовженні гри. Він також вперше застосував імовірнісні методи до демографічної статистики і показав, як розрахувати середню тривалість життя.

До цього ж періоду належать публікації англійських статистиків Джона Граунта (1662) і Вільяма Петті (1676, 1683). Обробивши дані більш ніж за століття, вони показали, що велика кількість демографічних характеристик лондонського населення, незважаючи на випадкові коливання, мають досить стійкий характер — наприклад, співвідношення кількості новонароджених хлопчиків і дівчаток рідко відхиляється від пропорції 14 до 13, невеликі коливання і відсотка смертності від конкретних випадкових причин. Ці дані підготували наукову громадськість до сприйняття нових ідей.

Граунт також вперше склав таблиці смертності — таблиці ймовірності смерті як функції віку. Питаннями теорії ймовірностей і її застосування до демографічної статистики зайнялися також Йоганн Худде і Ян де Вітт, які в 1671 року також склали таблиці смертності і використовували їх для обчислення розмірів довічної ренти. Детальніше дане коло питань було викладено у 1693 році Едмундом Галлеєм.

На книгу Гюйгенса спиралися, що з'явилися на початку XVIII століття, трактати П'єра де Монмора «Досвід дослідження азартних ігор» (фр. Essay d'analyse sur les jeux de hazard; опублікований в 1708 і перевиданий з доповненнями в 1713 році) і Якоба Бернуллі «Мистецтво припущень» (лат. Ars conjectandi; опублікований вже після смерті вченого, в тому ж 1713 році). Останній мав для теорії ймовірностей особливо велике значення.

Над трактатом «Мистецтво припущень» Якоб Бернуллі працював двадцять років, вже років за десять до публікації текст цієї праці у вигляді незакінченого рукопису став поширюватися по Європі, викликаючи великий інтерес. Трактат став першим систематичним викладом теорії ймовірностей. У цій книзі автор надав, зокрема, класичне визначення ймовірності події як відношення числа випадків, пов'язаних з цією подією, до загальної кількості випадків (у достовірної події ймовірність дорівнює одиниці, у неможливої — нулю). Систематично вивчена Бернуллі імовірнісна схема зараз називається біноміальним розподілом.

Раніше математики найчастіше оперували власе кількістю результатів; історики вважають, що заміна кількості на «частоту» (тобто поділ на загальну кількість випадків) була стимульована статистичними міркуваннями: частота, на відміну від кількості, зазвичай має тенденцію до стабілізації при збільшенні кількості спостережень. Визначення ймовірності «по Бернуллі» відразу стало загальноприйнятим, його відтворювали Абрахам де Муавр в книзі «Вчення про випадки» (1718) і всі наступні математики. Єдине важливе уточнення — про те, що всі «елементарні результати» зобов'язані бути різвноімовірними, — зробив П'єр-Симон Лаплас у 1812 році. Якщо для події неможливо підрахувати класичну ймовірність (наприклад, через відсутність можливості виділити рівноімовірні результати), то Бернуллі запропонував використовувати статистичний підхід, тобто оцінити ймовірність за результатами спостережень цієї події або пов'язаних з нею.

У першій частині свого трактату Бернуллі повністю передруковує книгу Гюйгенса, якій він дає найвищу оцінку, і істотно доповнює власними коментарями. Зокрема, він наводить загальну «формулу Бернуллі»: якщо ймовірність події дорівнює p, то ймовірність того, що в n випробуваннях подія трапиться m разів дорівнює ${\displaystyle C_{n}^{m}p^{m}(1-p)^{n-m}}$ . Далі Бернуллі докладно викладає комбінаторикиу і на її основі вирішує кілька завдань із випадковим вибором. В останній частині книги, що залишилася недописана, Бернуллі збирався розглянути економічні та інші практичні застосування теорії ймовірностей.

Величезне значення як для теорії ймовірностей, так і для науки загалом мав доведений Бернуллі перший варіант закону великих чисел (назву закону дав пізніше Пуассон). Цей закон пояснює, чому статистична частота при збільшенні числа спостережень зближується з теоретичним її значенням — ймовірністю, і тим самим пов'язує два різних визначення ймовірності. Надалі закон великих чисел працями багатьох математиків був значно узагальнений і уточнений; як виявилося, прагнення статистичної частоти до теоретичної відрізняється від прагнення до межі в аналізі — частота може значно відхилятися від очікуваної межі, і можна тільки стверджувати, що ймовірність таких відхилень з ростом кількості випробувань прямує до нуля. Водночас відхилення частоти від ймовірності також піддаються імовірнісному аналізу.

Трактат Якоба Бернуллі викликав різкий підйом інтересу до імовірнісних проблем і зростання числа досліджень нових завдань. Абрахам де Муавр опублікував кілька робіт, серед яких найбільш цікаві стаття «Про вимір випадковості, або ймовірності результатів в азартних іграх» (1711) і трактат «Вчення про випадки» (1718), що мав у XVIII столітті три видання. У цьому трактаті Муавр не тільки повністю вирішив згадувану вище «задачу про розорення гравця», а й оцінив для неї середню тривалість гри і ймовірності виграшу за вказану кількість ігор для кожного гравця. В іншій роботі, що називалася «Аналітична суміш», Муавр дав перший варіант теореми Муавра-Лапласа, що досліджує розподіл можливих відхилень статистичної частоти від ймовірності. Муавр розглянув лише випадок, коли ймовірність дорівнює 1/2, загальний же випадок для будь-якої ймовірності довів Лаплас. Ще одним досягненням Муавра стало перше введення в науку нормального розподілу (1733), яке з'явилося у нього як апроксимація біноміального розподілу.

Даніель Бернуллі, племінник засновника теорії ймовірностей, також зробив внесок у цю науку. Він, незалежно від Муавра, досліджував нормальний розподіл для помилок спостережень, першим застосував до імовірнісних задач методи математичного аналізу, опублікував перший з імовірнісних парадоксів (1738).

Наступний важливий крок зробив англійський математик Томас Сімпсон, який у процесі занять чисельним аналізом у книзі «Природа і закони випадку» (1740) фактично використовував третє (поряд із класичним і статистичними) визначення ймовірності — геометричне, придатне для дослідження безперервних випадкових величин із нескінченним числом значень. У задачі XXVI Сімпсон знайшов ймовірність того, що навмання кинутий на площину паралелепіпед зупиниться на заданій своєї грані.

Підхід Сімпсона розвинув Жорж-Луї де Бюффон, який у 1777 році навів класичний приклад завдання на геометричну ймовірність. Це була займавша згодом багатьох математиків «задача Бюффона»: площина розграфлена «в лінійку», на неї навмання кидається голка, потрібно знайти ймовірність того, що голка перетне лінію. Якщо довжина голки a менша, ніж відстань між лініями l, то шукана ймовірність дорівнює ${\displaystyle {\frac {2a}{\pi l}}}$. Ця формула була кілька разів перевірена експериментально, в тому числі самим Бюффоном, а в 1901 році італійський математик Маріо Лаццаріні (Mario Lazzarini) використовував її для визначення числа пі. Задача Бюффона, її аналіз і різні модифікації обговорювалися математиками багато років.

Була вирішена найважливіша задача розрахунку ймовірності для складних подій. Англійський математик Томас Баєс першим у чіткому вигляді навів теорему додавання ймовірностей для декількох несумісних подій і основоположні в теорії ймовірностей і статистиці «формули Баєса» (1763 рік, опубліковані посмертно). У сучасній термінології формули Баєса дозволяють ро��рахувати умовну ймовірність, а також уточнити розраховану ймовірність після отримання нових даних. Теорему множення ймовірностей раніше відкрив Муавр (1718 рік) і дав їй цілком сучасне, хоча і словесне формулювання: «ймовірність появи двох залежних подій дорівнює добутку ймовірності появи одного з них на ймовірність того, що інше повинно з'явитися, якщо перше з них вже з'явилося».

До середини XVIII століття аналіз ігор все ще привертає певний інтерес — наприклад, Леонард Ейлер дав докладний аналіз різних типів лотерей, але центром уваги математиків все більшою мірою стають демографічна статистика, страхування і оцінка помилок (вимірювання, округлення і т. д.). Статистиці і страхуванню Ейлер присвятив чимало робіт; він, зокрема, вирішував завдання: оцінити за статистичними таблицями, наскільки ймовірним є те, що людина у віці m років проживе ще n років.

У XIX столітті кількість робіт з теорії ймовірностей продовжувала зростати, були навіть компрометуючі науку спроби поширити її методи далеко за розумні межі — наприклад, на область моралі, психології, правозастосування та навіть богослов'я. Зокрема, валлійський філософ Річард Прайс, а слідом за ним і Лаплас, вважали за можливе розрахувати за формулами Баєса ймовірність майбутнього сходу сонця, Пуассон намагався провести імовірнісний аналіз справедливості судових вироків і достовірності показань свідків. Філософ Дж. С. Мілль у 1843 році, вказавши на подібні спекулятивні застосування, назвав обчислення ймовірностей «ганьбою математики». Ця та інші оцінки свідчили про недостатню строгість обґрунтування теорії ймовірностей.

Математичний апарат теорії ймовірностей тим часом продовжував удосконалюватися. Основною сферою її застосування в той період була математична обробка результатів спостережень, що містять випадкові похибки, а також розрахунки ризиків у страховій справі та інших статистичних параметрів. Серед головних прикладних задач теорії ймовірностей і математичної статистики XIX століття можна назвати такі:

• знайти ймовірність того, що сума незалежних випадкових величин з однаковим (відомим) законом розподілу знаходиться в заданих межах. Особливу важливість ця проблема представляла для теорії помилок вимірювання, в першу чергу для оцінки похибки спостережень;
• встановлення статистичної значущості відмінності випадкових значень або серій таких значень. Приклад: порівняння результатів застосування нового і старого видів ліків для прийняття рішення про те, чи дійсно нові ліки кращі;
• дослідження впливу заданого фактора на випадкову величину (факторний аналіз).

Уже до середини XIX століття формується імовірнісна теорія артилерійської стрільби. У більшості великих країн Європи були створені національні статистичні організації. В кінці століття область застосування імовірнісних методів почала успішно поширюватися на фізику, біологію, економіку, соціологію.

Карл Фрідріх Гаус, постійно займався астрономічними обчисленнями, розробив ймовірнісну методику роботи з вимірами, що містять похибки (1809). Він глибоко вивчив нормальний розподіл, показав, що він у багатьох практичних ситуаціях є граничним для випадкових значень, обґрунтував застосування методу найменших квадратів для оцінки вимірюваного значення і параметрів його можливого діапазону розкиду. Остаточну версію теорії Гаусс виклав у двох працях «Теорія комбінації спостережень, схильних до випадкових помилок» (1823, 1828). Хоча нормальний закон був відомий задовго до Гаусса, його внесок у теорію цього найважливішого розподілу настільки великий, що довгий час нормальний закон називали «законом Гаусса»; сучасний термін закріпився завдяки роботам Карла Пірсона в кінці XIX століття.

Основні досягнення теорії ймовірностей підсумовано в капітальній монографії Лапласа «Аналітична теорія ймовірностей» (1812 рік), яка завершила «класичний етап» розвитку цієї науки. У XIX столітті праця Лапласа мала у Франції три перевидання і була переведена на багато мов світу. Лаплас досліджував як дискретні, так і неперервні випадкові величини (ще не вводячи терміна «випадкова величина»), причому для неперервних дав ключове поняття щільності розподілу ймовірності, раніше неявно і обмежено використане Даніелєм Бернуллі. Інтегральне поняття функції розподілу виникло набагато пізніше (його в 1912 році ввів О. М. Ляпунов); загальний термін «випадкова величина» також, мабуть, вперше з'явився в роботах російської школи ймовірності. Введення щільності ймовірності та характеристичних функцій дозволило Лапласу застосувати для вирішення імовірнісних задач потужні аналітичні засоби, включаючи диференціальні рівняння з частинними похідними.

Лаплас навів формулу повної ймовірності для декількох несумісних «причин» (в сучасній термінології, «гіпотез»), довів ряд граничних теорем, в тому числі теорему Муавра — Лапласа і збіжність біноміального розподілу до нормального при збільшенні числа випробувань. Значна частина книги присвячена статистичним додаткам і вирішенням завдань. Для оцінки можливого діапазону значень вимірюваної величини Лаплас, як і Гаусс, рекомендував метод найменших квадратів.

Лаплас описав і своє розуміння сутності випадковості і ймовірності. На його думку, хід реальних процесів повністю зумовлений («детермінований»), випадковість з'являється лише в людському сприйнятті і тільки там, де людина не володіє повним знанням того, що відбувається:

Розум, якому були б відомі для якого-небудь даного моменту всі сили, що одушевляють природу, і відносне положення всіх її складових частин, якби ж він виявився достатньо великим, щоб підпорядкувати ці дані аналізу, охопив би в одній формулі рух найбільших тіл всесвіту нарівні з рухами найлегших атомів; не залишилося б нічого, що було б для нього недостовірно, і майбутнє, так само, як і минуле, постало б перед його поглядом.

Симеон Дені Пуассон в 1837 році узагальнив закон великих чисел Бернуллі, знявши умову про те, що ймовірність події в кожній грі одна і та ж; при цих нових умовах статистична частота буде сходитися до середнього арифметичного для ймовірностей окремих ігор. Він же опублікував формулу Пуассона, зручну для опису схеми Бернуллі в тому випадку, коли ймовірність події близька до нуля або до одиниці. Розподіл Пуассона («закон рідкісних подій») є одним з основних у прикладних задачах, наприклад, йому підкоряються радіоактивний розпад, народження трійні, статистика аварій і нещасних випадків.

Основна проблема в цій галузі така. Нехай послідовні вимірювання деякої величини дали n близьких, але нерівних значень. Мається на увазі, що систематичні помилки і залежність величини від часу вимірювання (скажімо, при обертанні небесного зводу) враховані, так що відмінність даних викликано чисто випадковими похибками. Треба за результатами вимірювань визначити найбільш правильну оцінку істинного значення досліджуваної величини.

Перше математичне дослідження цієї практично важливої (особливо в астрономії) теми зробив Томас Сімпсон (1755). Він виходив з невірної гіпотези, що похибкиви мірювання розподілені по «трикутному закону», але зробив правильний висновок — середнє арифметичне результатів вимірювання ближче до істинного значення, ніж окремий вимір. Даніель Бернуллі (1778) вважав, що щільність розподілу помилок є дугою окружності, але висновок Сімпсона підтвердив. Ідеї ​​Сімпсона розвинув І. Г. Ламберт, вперше застосував метод твірних функцій і метод максимальної вірогідності, пізніше узагальнений Р. Е. Фішером [53].

У XIX столітті Лаплас вказав, що спостережувані похибки вимірювання є зазвичай результатом підсумовування безлічі випадкових помилок, і тому їх розподіл має бути близьким до нормального. Замість середнього арифметичного він запропонував статистичну медіану. Однак майже одночасно був опублікований набагато більш практичний метод найменших квадратів Гаусса (1809), який і став загальновживаним. У 1853 році Коші виявив приклад розподілу, для якого середнє арифметичне є дуже поганою оцінкою. До кінця XIX століття статистична теорія обробки помилок була в основному завершена.

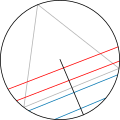
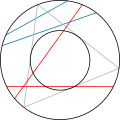
У 1889 році французький математик Жозеф Бертран у своєму курсі «Аналіз ймовірностей» запропонував ряд парадоксів, пов'язаних із геометричною ймовірністю. У кожному парадоксі різні тлумачення понять «навмання» або «узяте довільно» призводило до різних рішень завдань. Приклад одного з парадоксів Бертрана: знайти ймовірність того, що вибрана навмання хорда кола виявиться довшою сторони вписаного в це коло трикутника. При різних методах вибору хорди «навмання» виходять різні відповіді.

• 
  Метод 1
• 
  Метод 2
• 
  Метод 3

Обговорення парадоксів Бертрана сприяло уточненню підстав теорії ймовірностей і сенсу терміна «рівновірогідно».

До середини XIX століття практичне застосування теорії ймовірностей було в основному обмежено статистикою і наближеними обчисленнями, тому загальний термін «випадкова величина» з'явився досить пізно. Одним із перших випадкових процесів у фізиці став виявлений Робертом Броуном в 1827 році під мікроскопом хаотичний рух квіткового пилку, який плавав у воді («броунівський рух»). Його математична модель, проте, з'явилася тільки на початку XX століття (А. Ейнштейн, М. Смолуховський, Н. Вінер).

Перші фізичні імовірнісні моделі виникли в статистичній фізиці, яку розробили в другій половині XIX століття Л. Больцман, Д. К. Максвелл і Д. В. Гіббс. Больцман у серії робіт (1860-ті роки) показав, що термодинамічні закони мають ймовірносно-статистичний характер і пов'язані з переходом фізичних систем з менш ймовірного стану в більш ймовірний, причому мірою ймовірності є ентропія. Максвелл у ці ж роки вивів закон розподілу швидкостей молекул в газі, який дозволяє розрахувати енергію, довжину вільного пробігу й інші характеристики молекул. У 1902 році Гіббс опублікував монографію «Основні принципи статистичної механіки», що мала великий вплив на розвиток фізики. До кінця XIX століття величезне практичне значення імовірнісних методів стало загальновизнаним фактом.

У Російській імперії в першій половині XIX століття почали виникати власні серйозні дослідження з теорії ймовірностей. Перший навчальний курс почав читати С. Ревковський у Вільнюському університеті (1829 рік), там же в 1830 році була створена перша у Російській імперії кафедра теорії ймовірностей. У Петербурзькому університеті лекції з 1837 роки читав спочатку В. А. Анкудовіч, а з 1850 року — В. Я. Буняковський. Фундаментальний підручник «Підстави математичної теорії ймовірностей» Буняковский опублікував у 1846 році, і вигадана ним російська термінологія стала загальноприйнятою. У Московському університеті курс з'явився в 1850 році, лекції читав А. Ю. Давидов, майбутній президент Московського математичного товариства.

Статті по імовірнісним темам публікували багато математиків імперії, в тому числі М. В. Остроградський, М. Д. Брашман, М. І. Лобачевський, М. Є. Зернов. У значної частини цих робіт відчувається сильний вплив праць і поглядів Лапласа.

Першими російськими математиками світового рівня в теорії ймовірностей стали П. Л. Чебишев і його учні А. А. Марков і О. М. Ляпунов. Чебишев із самого початку своєї наукової кар'єри приділяв найбільшу увагу теорії ймовірностей (поряд з теорією чисел), а з 1860 року змінив Буняковского ��а кафедрі теорії ймовірностей і почав свій цикл лекцій. Він опублікував на цю тему лише чотири роботи, але фундаментального характеру. Особливо цікава його стаття «Про середні величини» (1866 рік), де наведено «нерівність Чебишева», пізніше посилене Марковим:${\displaystyle \mathbb {P} \left(|x-Mx|\geqslant k\sigma \right)\leqslant {\frac {1}{k^{2}}}}$

Ця формула означає, що ймовірність відхилення будь-якої випадкової величини x від її середнього значення (математичного очікування) Mx більш ніж на k стандартних відхилень (${\displaystyle \sigma }$) не перевищує ${\displaystyle {\frac {1}{k^{2}}}}$ . Наприклад, відхилення на 5 ${\displaystyle \sigma }$ має ймовірність 1/25, тобто 4 %.

Як наслідок своєї нерівності Чебишев отримав надзвичайно загальне формулювання закону великих чисел: якщо математичні очікування серії n випадкових величин і квадрати цих математичних очікувань обмежені в сукупності, то середнє арифметичне цих величин із ростом n сходиться до середнього арифметичного для їх математичних очікувань. З цієї теореми виходять як наслідки теореми Бернуллі і Пуассона; Чебишев вперше строго оцінив точність цих теорем та інших наближень.

У 1887 році з'явилася стаття Чебишева «Про дві теореми щодо ймовірностей». У цій роботі він встановив, що при деяких (досить загальних) умов виконується гранична теорема: сума великої кількості незалежних випадкових величин (наприклад, похибок вимірювання) розподілена приблизно за нормальним законом і тим точніше, чим більше доданків. Цей результат по своїй спільності далеко перекриває теорему Муавра — Лапласа і всі її аналоги. Пізніше А. А. Марков і О. М. Ляпунов уточнили і ще більш узагальнили дану теорему Чебишева.

Обидві згадані теореми Чебишева займають центральне місце в теорії ймовірностей. Особливо важлива та обставина, що Чебишев не тільки вказав граничний розподіл, але в обох випадках детально проаналізував межі можливих відхилень від цієї межі^[5].

Якщо Чебишев досліджував незалежні випадкові величини, то А. А. Марков у 1907 році розширив поле досліджень, розглядаючи і випадок, коли нове випадкове значення залежить від старого. Марков довів варіант закону великих чисел для деяких поширених типів залежних величин, ввівши в термінологію світової науки «ланцюги Маркова». Аналізу та класифікації цих ланцюгів Марков присвятив чимало робіт; ланцюги Маркова та марковські випадкові процеси застосовуються не тільки в математиці, але і в інших науках, таких як статистична фізика, квантова механіка, теорія автоматичного керування і багатьох інших. Маркову належить також розподіл усіх обґрунтувань методу найменших квадратів.

О. М. Ляпунову належить введення методу характеристичних функцій до вчення про граничні теореми теорії ймовірностей.

Ймовірність і статистика стали тісно пов'язані завдяки роботі над перевірками гіпотез Фішера і Неймана. Її результати зараз широко застосовуються в біологічних і психологічних експериментах та клінічних дослідженнях лікарських засобів. Наприклад гіпотеза, що препарат, як правило, ефективний, підвищує ймовірність розподілу, який можна було б спостерігати, якби гіпотеза була вірною. Якщо спостереження приблизно узгоджується з гіпотезою, то її вважають підтвердженою, а якщо ні — то гіпотеза відкидається.

Цю статтю треба вікіфікувати для відповідності стандартам якості Вікіпедії. Будь ласка, допоможіть додаванням доречних внутрішніх посилань або вдосконаленням розмітки статті. (лютий 2017)