Точка Лемуана

Точка Лемуана
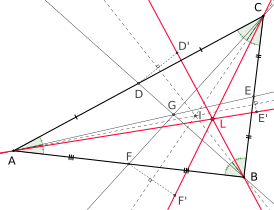Треугольник с тремя (голубыми) медианами, с тремя (зелеными) биссектрисами углов и с тремя (красными) симедианами . Симедианы пересекаются в точке Лемуана L, биссектрисы углов - в инцентре I, а медианы - в центроиде G.
Барицентрические координаты	${\displaystyle a^{2}:b^{2}:c^{2}}$
Трилинейные координаты	${\displaystyle a:b:c}$
Код ЭЦТ	X(6)
Связанные точки
Изогонально сопряженная	центроид
Изотомически сопряженная	третья точка Брокара

То́чка Лемуа́на (точка пересечения симедиан, точка Гребе, обозначается ${\displaystyle K}$ или ${\displaystyle L}$) — одна из замечательных точек треугольника.

У точки Лемуана существует три равносильных определения:

• точка пересечения прямых, соединяющих каждую вершину треугольника с точками пересечения касательных к описанной окружности, проведённых из двух других вершин.
• точка пересечения симедиан.
• точка пересечения прямых, соединяющих середины сторон треугольника с серединами соответствующих им высот.

Утверждение о равносильности первых двух определений называется теоремой о симедиане.

Доказательство

Пусть ${\displaystyle A_{1}}$ — точка пересечения касательных в вершинах ${\displaystyle B}$ и ${\displaystyle C}$ к описанной окружности, ${\displaystyle A_{M}}$ — середина стороны ${\displaystyle BC}$. Тогда, так как ${\displaystyle BC}$ — по��яра точки ${\displaystyle A_{1}}$ относительно описанной окружности, а ${\displaystyle A_{M}}$ — основание перпендикуляра на сторону ${\displaystyle BC}$ из центра описанной окружности. Из определения поляры следует, что точки ${\displaystyle A_{1}}$ и ${\displaystyle A_{M}}$ симметричны относительно окружности. Пусть точка ${\displaystyle A_{0}}$ — середина дуги ${\displaystyle BC}$ описанной окружности, не содержащей точки ${\displaystyle A}$. Тогда ${\displaystyle \angle A_{0}AA_{M}=\angle A_{0}AA_{1}}$, то есть прямая ${\displaystyle AA_{1}}$ и медиана ${\displaystyle AA_{M}}$ симметричны относительно биссектрисы ${\displaystyle AA_{0}}$. Аналогично симметричны медианам другие две прямые, построенные таким образом. Но их точка пересечения — точка Лемуана, а, значит, точка Лемуана изогонально сопряжена точке пересечения медиан и является точкой пересечения симедиан.

Шестиугольник Лемуана представляет собой шестиугольник, около которого можно описать окружность. Его вершинами являются шесть точек пересечениями сторон треугольника с тремя линиями, которые параллельны сторонам и которые проходят через его точку Лемуана. В любом треугольнике шестиугольник Лемуана находится внутри треугольника с тремя парами вершин, лежащих попарно на каждой стороне треугольника.

Лемуан доказал, что если прямые линии проходят через точку Лемуана параллельно сторонам треугольника, то шесть точек пересечения линий и сторон треугольника лежат на одной окружности, или что они лежат на окружности. ^[1]. Эта окружность теперь известна, как первый круг или окружность Лемуана, или просто как круг Лемуана.^[2]. Иными словами, шестиугольник Лемуана, определенный выше, является вписанным в окружность Лемуана.

Впервые точку Лемуана (Lemoine Point) обнаружил (1809) швейцарский геометр и тополог Симон Антуан Жан Люилье. Этой точке было посвящено исследование (1847) Эрнста Вильгельма Гребе (Grebe), в честь которого в Германии она называлась точкой Гребе (Grebe point). Точка названа в честь французского геометра Эмиля Лемуана, опубликовавшего доказательство существования точки (1873). Росс Хонсберегер (Ross Honsberger) назвал существование точки Лемуана "одним из драгоценных камней в короне современной геометрии".^[3]

• Сумма квадратов расстояний от точки на плоскости до сторон треугольника минимальна, когда эта точка является точкой Лемуана.
• Расстояния от точки Лемуана до сторон треугольника пропорциональны длинам сторон.
• Точка Лемуана является точкой пересечения медиан треугольника, образованного проекциями точки Лемуана на стороны. Более того, такая точка единственна.
• Точка Лемуана является точкой Жергонна треугольника, образованного касательными к описанной окружности в вершинах треугольника. Этот треугольник называется тангенциальным треугольником.
• Точка Лемуана изогонально сопряжена точке пересечения медиан
• Точка Лемуана изотомически сопряжена его точке Брокара (третьей, в энциклопедии центров треугольника обозначенной как Х(76) ).
• Точка Лемуана является антиперспектором описанной окружности. Трилинейные поляры точек на описанной окружности проходят через точку Лемуана.

• Окружность, построенная на отрезке ${\displaystyle OK}$ (${\displaystyle O}$ — центр описанной окружности) как на диаметре, содержит точки Брокара. Эта окружность называется окружностью Брокара.
• Прямая ${\displaystyle OK}$ называется осью Брокара. Она содержит точки Аполлония и изогонально сопряжена гиперболе Киперта.
• Две точки Торричелли и точка Лемуана лежат на одной прямой.
• Точки Аполлония лежат на прямой, соединяющей центр описанной окружности с точкой Лемуана. Эта прямая называется осью Брокара.
• При проективных преобразованиях, сохраняющих описанную окружность треугольника, точка Лемуана будет переходить в точку Лемуана образа этого треугольника.
• Эллипс с фокусами в точках Брокара называется эллипсом Брокара. Его перспектором служит точка Лемуана ^[4].

• Если провести через точку Лемуана отрезки, параллельные сторонам треугольника, с концами на сторонах, то концы этих отрезков будут лежать на одной окружности (на первой окружности Лемуана). Центром первой окружности Лемуана является середина отрезка, который соединяет центр описанной окружности треугольника с точкой Лемуана. ^[5]
• Если провести через точку Лемуана отрезки, антипараллельные сторонам треугольника, с концами на сторонах, то концы этих отрезков будут лежать на одной окружности (на второй окружности Лемуана). Точка Лемуана будет её центром. ^[6]

• Трилинейные координаты точки Лемуана — ${\displaystyle (a:b:c)}$,
• барицентрические — ${\displaystyle (a^{2}:b^{2}:c^{2})}$.

• Точка Лемуана