Poliedru uniform

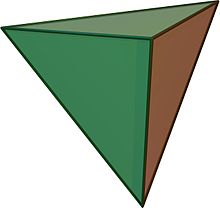
Un poliedru uniform are poligoane regulate ca fețe și este tranzitiv pe vârfuri (adică, există o izometrie care aplică orice vârf pe oricare altul). Rezultă că toate vârfurile sunt congruente.

Poliedrele uniforme pot fi regulate (dacă sunt și tranzitive pe fețe și muchii), cvasiregulate (dacă sunt tranzitive pe muchii, dar nu și pe fețe) sau semiregulate (dacă nu sunt tranzitive nici pe muchii, nici pe fețe). Fețele și vârfurile nu trebuie să fie convexe, așa că multe dintre poliedrele uniforme sunt și poliedre stelate.

Există două clase infinite de poliedre uniforme, împreună cu alte 75 de poliedre:

Clase infinite:
- prisme,
- antiprisme;
Convexe:
- 5 poliedre platonice: poliedre convexe regulate,
- 13 poliedre arhimedice: 2 poliedre convexe cvasiregulate și 11 semiregulate;
Stelate (neconvexe):
- 4 poliedre Kepler–Poinsot: poliedre neconvexe regulate,
- 53 poliedre stelate uniforme: 5 poliedre cvasiregulate și 48 semiregulate.

Există, de asemenea, multe poliedre uniforme degenerate, cu perechi de muchii care coincid, inclusiv unul găsit de John Skilling numit marele dirombidodecaedru disnub (figura lui Skilling).

Poliedrele duale ale poliedrelor uniforme sunt tranzitive pe fețe (izoedrice) și au figurile vârfurilor regulate, și sunt în general clasificate în paralel cu poliedrul lor dual (uniform). Dualul unui poliedru regulat este regulat, în timp ce dualul unui poliedru arhimedic este un poliedru Catalan.

Conceptul de poliedru uniform este un caz special al conceptului de politop uniform, care se aplică și formelor din spațiile din dimensiuni superioare (sau din dimensiuni inferioare).

Definiție

Păcatul originar din teoria poliedrelor începe cu Euclid și prin Kepler, Poinsot, Cauchy și mulți alții continuă să afecteze toate lucrările pe această temă (inclusiv cele ale autorului de față). Provine din faptul că utilizarea tradițională a termenului „poliedre regulate” a fost, și este, contrară sintaxei și logicii: cuvintele par să sugereze că avem de-a face cu obiecte pe care le numim „poliedre”, cu acele cazuri particulare care merită să fie numite „regulate”. Dar în fiecare etapă — Euclid, Kepler, Poinsot, Hess, Brückner, ... — autorii nu au reușit să definească ce sunt „poliedrele” printre care se găsesc cele „regulate”. Branko Grünbaum (1994)

Coxeter, Longuet-Higgins & Miller (1954) definesc poliedrele uniforme drept poliedre tranzitive pe vârfuri, cu fețe regulate. Ei definesc un poliedru ca fiind o mulțime finită de poligoane astfel încât fiecare latură a unui poligon să fie o latură a doar unui alt poligon, astfel încât nicio submulțime proprie nevidă a poligoanelor să aibă aceeași proprietate. Prin poligon se înțelege implicit un poligon în spațiul euclidian tridimensional; acestora le este permis să fie dispuse într-o formă neconvexă și să se intersecteze unul cu altul.

Există câteva generalizări ale conceptului de poliedru uniform. Dacă se renunță la presupunerea de conectivitate, atunci se obțin compuși uniformi, care pot fi considerați ca o reuniune de poliedre, cum ar fi compusul de cinci cuburi. Dacă se renunță la condiția ca realizarea poliedrului să nu fie degenerată, atunci se obține așa-numitul poliedru degenerat uniform. Acestea necesită o definiție mai generală a poliedrelor. Grünbaum (1994) a dat o definiție destul de complicată a unui poliedru, în timp ce McMullen & Schulte (2002) a dat o definiție mai simplă și mai generală a unui poliedru: în terminologia lor, un poliedru este un politop abstract bidimensional cu o realizare tridimensională nedegenerată. Aici un politop abstract este o poziție a „fețelor” sale care îndeplinește diferite condiții, o realizare este o funcție a vârfurilor sale într-un anumit spațiu, iar realizarea se numește nedegenerată dacă oricare două fețe distincte ale politopului abstract au realizări distincte.

Unele dintre modalitățile prin care pot degenera sunt următoarele:

Fețe ascunse. Unele poliedre au fețe ascunse, în sensul că niciun punct al interiorului lor nu poate fi văzut din exterior. Acestea nu sunt considerate de obicei poliedre uniforme.
Compuși degenerați. Unele poliedre au muchii multiple și fețele lor sunt fețele a două sau mai multe poliedre, deși acestea nu sunt compuși în sensul anterior, deoarece poliedrele au muchii comune.
Acoperiri duble. Există unele poliedre neorientabile care au acoperiri duble care satisfac definiția unui poliedru uniform. Acolo acoperirile duble au fețe, laturi și vârfuri dublate. De obicei nu sunt considerate poliedre uniforme.
Fețe duble. Există mai multe poliedre cu fețe duble produse prin construcția Wythoff. Mulți autori nu admit fețele duble și le elimină din construcție.
Margini duble. Figura Skilling are proprietatea că are margini duble (ca în poliedrele uniforme degenerate), dar fețele sale nu pot fi notate ca o reuniune a două poliedre uniforme.

Istoric

Poliedre convexe regulate

Poliedrele platonice datează din timpul grecilor clasici și au fost studiate de pitagoricienii, Platon (c. 424–348 î.Hr.), Theaetetus (c. 417–369 î.Hr.), Timaeus din Locri (c. 420–380 î.Hr.) și Euclid (323–285 î.Hr.). Etruscii au descoperit dodecaedrul regulat înainte de 500 î.Hr.^[1]

Poliedre convexe uniforme neregulate

Cuboctaedrul a fost cunoscut de Platon.
Arhimede (287–212 î.Hr.) a descoperit toate cele 13 poliedre arhimedice. Lucrarea sa originală despre acest subiect s-a pierdut, dar Pappus din Alexandria (c. 290–350) a menționat o listă a lui Arhimede cu cele 13 poliedre.
Piero della Francesca (1415–1492) a redescoperit cinci poliedre trunchiate ale poliedrelor platonice: tetraedrul, octaedrul trunchiat, cubul trunchiat, dodecaedrul trunchiat și icosaedrul trunchiat, și a inclus ilustrări și calcule ale proprietăților lor metrice în cartea sa De quinque corporibus regularibus (română Despre cele cinci corpuri regulate). În altă carte a scris despre cuboctaedru.^[2]
Luca Pacioli a plagiat în De divina proportione (română Proporția divină) din 1509 lucrarea lui della Francesca, adăugând rombicuboctaedrul, pe care l-a numit icosihexaedru după cele 26 de fețe ale sale, și care a fost desenat de Leonardo da Vinci.
Johannes Kepler (1571–1630) a fost primul care a publicat în 1619 lista completă a poliedrelor arhimedice și a identificat familiile infinite de prisme și antiprisme uniforme.

Poliedre stelate regulate

Kepler a descoperit în 1619 două din poliedrele Kepler–Poinsot regulate iar Louis Poinsot a descoperit alte două în 1809. Augustin Cauchy (1789–1857) a demonstrat că acestea sunt toate, iar numele lor a fost dat de Arthur Cayley (1821–1895).

Celelalte 53 de poliedre stelate neregulate

Din restul de 53, Edmund Hess (1878) a descoperit două, Albert Badoureau (1881) a descoperit încă 36 și, independent, Pitsch (1881) a descoperit 18, din care 3 nu fuseseră descoperite înainte. Împreună acestea erau 41 de poliedre.
H.S.M. Coxeter a descoperit restul de 12 în colaborare cu J. C. P. Miller (1930–1932) dar nu le-a publicat. M.S. Longuet-Higgins și H.C. Longuet-Higgins au descoperit independent 11 din ele. Lesavre și Mercier au descoperit 5 din ele în 1947.
Coxeter, Longuet-Higgins & Miller (1954) a publicat lista poliedrelor uniforme.
Sopov (1970) a demonstrat conjectura lor că lista era completă.
În 1974 Magnus Wenninger a publicat în cartea sa Polyhedron models (română Modele de poliedre), lista celor 75 de poliedre uniforme neprismatice, cu mai multe denumiri nepublicate anterior date de Norman Johnson.
Skilling (1975) a demonstrat independent completitudinea listei și a arătat că dacă definiția poliedrului uniform este relaxată pentru a permite muchiilor să coincidă, atunci există doar o singură posibilitate suplimentară.
În 1987, Edmond Bonan a trasat toate poliedrele uniforme și dualele lor în 3D, cu un program Turbo Pascal numit Polyca: aproape toate acestea au fost prezentate în cadrul Congresului Uniunii Stereoscopice Internaționale desfășurat la Congress Theatre, Eastbourne, Regatul Unit.^[3]
În 1993 Zvi Har'El a realizat o construcție caleidoscopică completă a poliedrelor uniforme și a dualelor lor cu un program de calculator numit Kaleido și le-a rezumat în articolul Uniform Solution for Uniform Polyhedra (română Soluție uniformă pentru poliedre uniforme), ilustrat cu 80 de figuri.^[4]
Tot în 1993, R. Mäder a portat această soluție Kaleido la Mathematica cu un sistem de indexare ușor diferit.^[5]
În 2002 Peter W. Messer a descoperit un set minim de expresii pentru determinarea principalelor cantități combinatorice și metrice ale oricărui poliedru uniform (și ale dualului său) dat doar de simbolul său Wythoff.^[6]

Poliedre stelate uniforme

Cele 57 de forme neconvexe neprismatice, cu excepția marelui dirombicosidodecaedru, sunt compilate după construcțiile Wythoff din triunghiurile Schwarz.

Forme convexe prin construcție Wythoff

Exemple de forme de cub și octaedru

Poliedrele uniforme convexe pot fi denumite după operațiile construcției Wythoff în forme regulate.

Mai detaliat, poliedrul uniform convex este dat mai jos de construcția Wythoff în cadrul fiecărui grup de simetrie.

În cadrul construcției Wythoff, există repetări create de forme cu simetrie inferioară. Cubul este atât un poliedru regulat cât și o prismă pătrată. Octaedrul este un poliedru regulat și o antiprismă triunghiulară. Octaedrul este, de asemenea, un tetraedru rectificat. Multe poliedre apar repetat, din diferite surse de construcție și sunt colorate diferit.

Construcția Wythoff se aplică în mod egal poliedrelor uniforme și pavărilor uniforme ale suprafeței unei sfere, deci sunt date imagini ale ambelor. Pavările sferice incluzând mulțimile de hosoedre și diedre, care sunt poliedre degenerate.

Aceste grupuri de simetrie sunt formate din reflexiile grupurilor de puncte în spațiul tridimensional, fiecare reprezentat printr-un triunghi fundamental (p q r), unde p > 1, q > 1, r > 1 și 1/p + 1/q + 1/r < 1.

Simetrie tetraedrică (3 3 2) – ordinul 24
Simetrie octaedrică (4 3 2) – ordinul 48
Simetrie icosaedrică (5 3 2) – ordinul 120
Simetrie diedrală (n 2 2), pentru n = 3,4,5,... – ordinul 4n

Restul formelor nereflexive sunt construite prin operațiuni de alternare aplicate poliedrelor cu un număr par de muchii.

Împreună cu prismele și simetria diedrală a acestora, procesul de construcție sferic Wythoff adaugă două clase regulate care devin degenerate ca poliedre: diedrele și hosoedrele, prima având doar două fețe, iar a doua doar două vârfuri. Trunchierea hosoedrelor regulate creează prismele.

Dedesubt, poliedrele uniforme convexe sunt numerotate 1–18 pentru formele neprismatice așa cum sunt prezentate în tabele prin forma de simetrie.

Pentru setul infinit de forme prismatice, acestea sunt grupate în patru familii:

Hosoedre H_2... (doar ca pavări sferice)
Diedre D_2... (doar ca pavări sferice)
Prisme P_3... (hosoedre trunchiate)
Antiprisme A_3... (prisme snub)

Tabele rezumative

Nume Johnson	Inițial	Trunchiat	Rectificat	Bitrunchiat (dual tr.)	Birectificat (dual)	Cantelat	Omnitrunchiat (cantitrunchiat)	Snub
Diagramă Coxeter
Simbol Schläfli extins	${\begin{Bmatrix}p,q\end{Bmatrix}}$	$t{\begin{Bmatrix}p,q\end{Bmatrix}}$	${\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}q,p\end{Bmatrix}}$	${\begin{Bmatrix}q,p\end{Bmatrix}}$	$r{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$s{\begin{Bmatrix}p\\q\end{Bmatrix}}$
	{p,q}	t{p,q}	r{p,q}	2t{p,q}	2r{p,q}	rr{p,q}	tr{p,q}	sr{p,q}
	t₀{p,q}	t_0,1{p,q}	t₁{p,q}	t_1,2{p,q}	t₂{p,q}	t_0,2{p,q}	t_0,1,2{p,q}	ht_0,1,2{p,q}
Simbol Wythoff (p q 2)	q \| p 2	2 q \| p	2 \| p q	2 p \| q	p \| q 2	p q \| 2	p q 2 \|	\| p q 2
Figura vârfului	p^q	q.2p.2p	(p.q)²	p.2q.2q	q^p	p.4.q.4	4.2p.2q	3.3.p.3.q
Tetraedrică (3 3 2)	3.3.3	3.6.6	3.3.3.3	3.6.6	3.3.3	3.4.3.4	4.6.6	3.3.3.3.3
Octaedrică (4 3 2)	4.4.4	3.8.8	3.4.3.4	4.6.6	3.3.3.3	3.4.4.4	4.6.8	3.3.3.3.4
Icosaedrică (5 3 2)	5.5.5	3.10.10	3.5.3.5	5.6.6	3.3.3.3.3	3.4.5.4	4.6.10	3.3.3.3.5

Exemple de simetrii diedrale

Sfera nu este tăiată, doar pavarea este tăiată. Pe o sferă, o muchie este un arc de cerc mare, cea mai scurtă cale între cele două vârfuri ale sale. Prin urmare, un digon ale cărui vârfuri nu sunt opuse polar este plat: arată ca o muchie.

(p 2 2)	Inițial	Trunchiat	Rectificat	Bitrunchiat (dual tr.)	Birectificat (dual)	Cantelat	Omnitrunchiat (cantitrunchiat)	Snub
Diagramă Coxeter
Simbol Schläfli extins	${\begin{Bmatrix}p,2\end{Bmatrix}}$	$t{\begin{Bmatrix}p,2\end{Bmatrix}}$	${\begin{Bmatrix}p\\2\end{Bmatrix}}$	$t{\begin{Bmatrix}2,p\end{Bmatrix}}$	${\begin{Bmatrix}2,p\end{Bmatrix}}$	$r{\begin{Bmatrix}p\\2\end{Bmatrix}}$	$t{\begin{Bmatrix}p\\2\end{Bmatrix}}$	$s{\begin{Bmatrix}p\\2\end{Bmatrix}}$
	{p,2}	t{p,2}	r{p,2}	2t{p,2}	2r{p,2}	rr{p,2}	tr{p,2}	sr{p,2}
	t₀{p,2}	t_0,1{p,2}	t₁{p,2}	t_1,2{p,2}	t₂{p,2}	t_0,2{p,2}	t_0,1,2{p,2}	ht_0,1,2{p,2}
Simbol Wythoff	2 \| p 2	2 2 \| p	2 \| p 2	2 p \| 2	p \| 2 2	p 2 \| 2	p 2 2 \|	\| p 2 2
Figura vârfului	p²	2.2p.2p	p.2.p.2	p.4.4	2^p	p.4.2.4	4.2p.4	3.3.3.p
Diedrală (2 2 2)	{2,2}	2.4.4	2.2.2.2	4.4.2	2.2	2.4.2.4	4.4.4	3.3.3.2
Diedrală (3 2 2)	3.3	2.6.6	2.3.2.3	4.4.3	2.2.2	2.4.3.4	4.4.6	3.3.3.3
Diedrală (4 2 2)	4.4	2.8.8	2.4.2.4	4.4.4	2.2.2.2	2.4.4.4	4.4.8	3.3.3.4
Diedrală (5 2 2)	5.5	2.10.10	2.5.2.5	4.4.5	2.2.2.2.2	2.4.5.4	4.4.10	3.3.3.5
Diedrală (6 2 2)	6.6	2.12.12	2.6.2.6	4.4.6	2.2.2.2.2.2	2.4.6.4	4.4.12	3.3.3.6

(3 3 2) T_d simetrie tetraedrică

Simetria tetraedrică a sferei generează 5 poliedre uniforme și o a 6-a formă printr-o operație snub.

Simetria tetraedrică este reprezentată de un triunghi fundamental cu un vârf cu două oglindiri și două vârfuri cu trei oglindiri, reprezentate de simbolul (3 3 2). Poate fi reprezentată și de grupul Coxeter A₂ sau [3,3], sau de o diagramă Coxeter: .

Există 24 de triunghiuri, vizibile în imaginile de alături pe fețele hexaedrului tetrakis și în triunghiurile colorate alternativ pe o sferă.

#	Nume	Graf A₃	Graf A₂	Imagine	Pavare	Figura vârfului	Simbol Coxeter și Schläfli	Numărul fețelor după poziție			Numărul elementelor
#	Nume	Graf A₃	Graf A₂	Imagine	Pavare	Figura vârfului	Simbol Coxeter și Schläfli	Poz. 2 [3] (4)	Poz. 1 [2] (6)	Poz. 0 [3] (4)	Fe- țe	Mu- chii	Vâr- furi
1	Tetraedru						{3,3}	{3}			4	6	4
[1]	Tetraedru birectificat (tetraedru)						t₂{3,3}={3,3}			{3}	4	6	4
2	Tetraedru rectificat, Tetratetraedru (octaedru)						t₁{3,3}=r{3,3}	{3}		{3}	8	12	6
3	Tetraedru trunchiat						t_0,1{3,3}=t{3,3}	{6}		{3}	8	18	12
[3]	Tetraedru bitrunchiat (tetraedru trunchiat)						t_1,2{3,3}=t{3,3}	{3}		{6}	8	18	12
4	Tetraedru cantelat, Rombitetratetraedru (cuboctaedru)						t_0,2{3,3}=rr{3,3}	{3}	{4}	{3}	14	24	12
5	Tetraedru omnitrunchiat, Tetratetraedru trunchiat (octaedru trunchiat)						t_0,1,2{3,3}=tr{3,3}	{6}	{4}	{6}	14	36	24
6	Tetratetraedru snub (icosaedru)						sr{3,3}	{3}	2 {3}	{3}	20	30	12

(4 3 2) O_h simetrie octaedrică

Simetria octaedrică a sferei generează 7 poliedre uniforme și alt 7 prin alternare. Șase din aceste forme sunt repetări ale simetriei tetraedrice din tabelul anterior.

Simetria octaedrică este reprezentată de un triunghi fundamental (4 3 2) având oglindiri în fiecare vârf. Poate fi reprezentată și de grupul Coxeter B₂ sau [4,3], sau de o diagramă Coxeter: .

Există 48 de triunghiuri, vizibile în imaginile de alături pe fețele dodecaedrului disdiakis și în triunghiurile colorate alternativ pe o sferă.

#	Nume	Graf B₃	Graf B₂	Imagine	Pavare	Figura vârfului	Simbol Coxeter și Schläfli	Numărul fețelor după poziție			Numărul elementelor
#	Nume	Graf B₃	Graf B₂	Imagine	Pavare	Figura vârfului	Simbol Coxeter și Schläfli	Poz. 2 [4] (6)	Poz. 1 [2] (12)	Poz. 0 [3] (8)	Fe- țe	Mu- chii	Vâr- furi
7	Cub						{4,3}	{4}			6	12	8
[2]	Octaedru						{3,4}			{3}	8	12	6
[4]	Cub rectificat, Octaedru rectificat (cuboctaedru)						{4,3}	{4}		{3}	14	24	12
8	Cub trunchiat						t_0,1{4,3}=t{4,3}	{8}		{3}	14	36	24
[5]	Octaedru trunchiat						t_0,1{3,4}=t{3,4}	{4}		{6}	14	36	24
9	Cub cantelat, Octaedru cantelat, Rombicuboctaedru						t_0,2{4,3}=rr{4,3}	{4}	{4}	{3}	26	48	24
10	Cub omnitrunchiat, Octaedru omnitrunchiat, Cuboctaedru trunchiat						t_0,1,2{4,3}=tr{4,3}	{8}	{4}	{6}	26	72	48
[6]	Octaedru snub (icosaedru)						= s{3,4}=sr{3,3}		{3}	{3}	20	30	12
[1]	Semicub (tetraedru)						= h{4,3}={3,3}	¹/₂ {3}			4	6	4
[2]	Cub cantic (tetraedru trunchiat)						= h₂{4,3}=t{3,3}	¹/₂ {6}		¹/₂ {3}	8	18	12
[4]	(cuboctaedru)						= rr{3,3}				14	24	12
[5]	(octaedru trunchiat)						= tr{3,3}				14	36	24
[9]	Octaedru cantic snub (rombicuboctaedru)						s₂{3,4}=rr{3,4}				26	48	24
11	Cuboctaedru snub						sr{4,3}	{4}	2 {3}	{3}	38	60	24

(5 3 2) I_h simetrie icosaedrică

Simetria icosaedrică a sferei generează 7 poliedre uniforme și încă 1 prin alternare. Doar unul este o repetare a simetriei tetraedrice și octaedriece din tabelele anterioare.

Simetria icosaedrică este reprezentată de un triunghi fundamental (5 3 2) având oglindiri în fiecare vârf. Poate fi reprezentată și de grupul Coxeter G₂ sau [5,3], sau de o diagramă Coxeter: .

Există 120 de triunghiuri, vizibile în imaginile de alături pe fețele triacontaedrului disdiakis și în triunghiurile colorate alternativ pe o sferă.

#	Nume	Graf (A₂) [6]	Graf (H₃) [10]	Imagine	Pavare	Figura vârfului	Simbol Coxeter și Schläfli	Numărul fețelor după poziție			Numărul elementelor
#	Nume	Graf (A₂) [6]	Graf (H₃) [10]	Imagine	Pavare	Figura vârfului	Simbol Coxeter și Schläfli	Poz. 2 [5] (12)	Poz. 1 [2] (30)	Poz. 0 [3] (20)	Fe- țe	Mu- chii	Vâr- furi
12	Dodecaedru						{5,3}	{5}			12	30	20
[6]	Icosaedru						{3,5}			{3}	20	30	12
13	Dodecaedru rectificat, Icosaedru rectificat, Icosidodecaedru						t₁{5,3}=r{5,3}	{5}		{3}	32	60	30
14	Dodecaedru trunchiat						t_0,1{5,3}=t{5,3}	{10}		{3}	32	90	60
15	Icosaedru trunchiat						t_0,1{3,5}=t{3,5}	{5}		{6}	32	90	60
16	Dodecaedru cantelat, Icosaedru cantelat, Rombicosidodecaedru						t_0,2{5,3}=rr{5,3}	{5}	{4}	{3}	62	120	60
17	Dodecaedru omnitrunchiat, Icosaedru omnitrunchiat, Icosidodecaedru trunchiat						t_0,1,2{5,3}=tr{5,3}	{10}	{4}	{6}	62	180	120
18	Icosidodecaedru snub						sr{5,3}	{5}	2 {3}	{3}	92	150	60

(p 2 2) Familia prismelor [p,2], I₂(p) (D_ph simetrie diedrală)

Simetria diedrală a sferei generează două mulțimi infinite de poliedre uniforme, prisme și antiprisme și alte două mulțimi infinite de poliedre degenerate, hosoedrele și diedrele care există ca pavări pe sferă.

Simetria diedrală este reprezentată de triunghiul fundamental (p 2 2) având oglindiri în fiecare vârf. Poate fi reprezentat de grupul Coxeter I₂(p) sau [n,2], precum și de o diagramă Coxeter prismatică: .

Mai jos sunt primele cinci simetrii diedrale: D₂ ... D₆. Simetria diedrală D_p are ordinul 4n, reprezintă fețele unei bipiramide, iar pe ecuatorul unei sfere un cerc de longitudine cu n arce de longitudine la distanțe egale.

(2 2 2) Simetrie diedrală

Există 8 triunghiuri fundamentale, vizibile pe fețele bipiramidei pătrate (octaedru) și triunghiuri colorate alternativ pe o sferă.

#	Nume	Imagine	Pavare	Figura vârfului	Simbol Coxeter și Schläfli	Numărul fețelor după poziție			Numărul elementelor
#	Nume	Imagine	Pavare	Figura vârfului	Simbol Coxeter și Schläfli	Poz. 2 [2] (2)	Poz. 1 [2] (2)	Poz. 0 [2] (2)	Fe- țe	Mu- chii	Vâr- furi
D₂ H₂	Diedru digonal, hosoedru digonal				{2,2}	{2}			2	2	2
D₄	Diedru digonal trunchiat (diedru pătrat)				t{2,2}={4,2}	{4}			2	4	4
P₄ [7]	Diedru digonal omnitrunchiat (cub)				t_0,1,2{2,2}=tr{2,2}	{4}	{4}]	{4}	6	12	8
A₂ [1]	Diedru digonal snub (tetraedru)				sr{2,2}		2 {3}		4	6	4

(3 2 2) D_3h simetrie diedrală

Există 12 triunghiuri fundamentale, vizibile pe fețele bipiramidei hexagonale și triunghiuri colorate alternativ pe o sferă.

#	Nume	Imagine	Pavare	Figura vârfului	Simbol Coxeter și Schläfli	Numărul fețelor după poziție			Numărul elementelor
#	Nume	Imagine	Pavare	Figura vârfului	Simbol Coxeter și Schläfli	Poz. 2 [3] (2)	Poz. 1 [2] (3)	Poz. 0 [2] (3)	Fe- țe	Mu- chii	Vâr- furi
D₃	Diedru trigonal				{3,2}	{3}			2	3	3
H₃	Hosoedru trigonal				{2,3}			{2}	3	3	2
D₆	Diedru trigonal trunchiat (diedru hexagonal)				t{3,2}	{6}			2	6	6
P₃	Hosoedru trigonal trunchiat (prismă triunghiulară)				t{2,3}	{3}	{4}		5	9	6
P₆	Diedru trigonal omnitrunchiat (Prismă hexagonală)				t_0,1,2{2,3}=tr{2,3}	{6}	{4}	{4}	8	18	12
A₃ [2]	Diedru trigonal snub (antiprismă triunghiulară), (Octaedru)				sr{2,3}	{3}	2 {3}		8	12	6
P₃	Diedru trigonal snub cantic (prismă triunghiulară)				s₂{2,3}=t{2,3}				5	9	6

(4 2 2) D_4h simetrie diedrală

Există 16 triunghiuri fundamentale, vizibile pe fețele bipiramidei octogonale și triunghiuri colorate alternativ pe o sferă.

#	Nume	Imagine	Pavare	Figura vârfului	Simbol Coxeter și Schläfli	Numărul fețelor după poziție			Numărul elementelor
#	Nume	Imagine	Pavare	Figura vârfului	Simbol Coxeter și Schläfli	Poz. 2 [4] (2)	Poz. 1 [2] (4)	Poz. 0 [2] (4)	Fe- țe	Mu- chii	Vâr- furi
D₄	Diedru pătrat				{4,2}	{4}			2	4	4
H₄	Hosoedru pătrat				{2,4}			{2}	4	4	2
D₈	Diedru pătrat trunchiat (diedru octogonal)				t{4,2}	{8}			2	8	8
P₄ [7]	Hosoedru pătrat trunchiat (cub)				t{2,4}	{4}	{4}		6	12	8
D₈	Diedru pătrat omnitrunchiat (prismă octogonală)				t_0,1,2{2,4}=tr{2,4}	{8}	{4}	{4}	10	24	16
A₄	Diedru pătrat snub (antiprismă pătrată)				sr{2,4}	{4}	2 {3}		10	16	8
P₄ [7]	Diedru pătrat snub cantic (cub)				s₂{4,2}=t{2,4}				6	12	8
A₂ [1]	Hosoedru pătrat snub (antiprismă digonală), (tetraedru)				s{2,4}=sr{2,2}				4	6	4

(5 2 2) D_5h simetrie diedrală

Există 20 triunghiuri fundamentale, vizibile pe fețele bipiramidei decagonale și triunghiuri colorate alternativ pe o sferă:

#	Nume	Imagine	Pavare	Figura vârfului	Simbol Coxeter și Schläfli	Numărul fețelor după poziție			Numărul elementelor
#	Nume	Imagine	Pavare	Figura vârfului	Simbol Coxeter și Schläfli	Poz. 2 [5] (2)	Poz. 1 [2] (5)	Poz. 0 [2] (5)	Fe- țe	Mu- chii	Vâr- furi
D₅	Diedru pentagonal				{5,2}	{5}			2	5	5
H₅	Hosoedru pentagonal				{2,5}			{2}	5	5	2
D₁₀	Diedru pentagonal trunchiat (diedru decagonal)				t{5,2}	{10}			2	10	10
P₅	Hosoedru pentagonal trunchiat (prismă pentagonală)				t{2,5}	{5}	{4}		7	15	10
P₁₀	Diedru pentagonal omnitrunchiat (prismă decagonală)				t_0,1,2{2,5}=tr{2,5}	{10}	{4}	{4}	12	30	20
A₅	Diedru pentagonal snub (antiprismă pentagonală)				sr{2,5}	{5}	2 {3}		12	20	10
P₅	Diedru pentagonal snub cantic (prismă pentagonală)				s₂{5,2}=t{2,5}				7	15	10

(6 2 2) D_6h simetrie diedrală

Există 24 triunghiuri fundamentale, vizibile pe fețele bipiramidei dodecagonale și triunghiuri colorate alternativ pe o sferă.

#	Nume	Imagine	Pavare	Figura vârfului	Simbol Coxeter și Schläfli	Numărul fețelor după poziție			Numărul elementelor
#	Nume	Imagine	Pavare	Figura vârfului	Simbol Coxeter și Schläfli	Poz. 2 [6] (2)	Poz. 1 [2] (6)	Poz. 0 [2] (6)	Fe- țe	Mu- chii	Vâr- furi
D₆	Diedru hexagonal				{6,2}	{6}			2	6	6
H₆	Hosoedru hexagonal				{2,6}			{2}	6	6	2
D₁₂	Diedru hexagonal trunchiat (diedru dodecagonal)				t{6,2}	{12}			2	12	12
H₆	Hosoedru hexagonal trunchiat (prismă hexagonală)				t{2,6}	{6}	{4}		8	18	12
P₁₂	Diedru hexagonal omnitrunchiat (prismă dodecagonală)				t_0,1,2{2,6}=tr{2,6}	{12}	{4}	{4}	14	36	24
A₆	Diedru hexagonal snub (antiprismă hexagonală)				sr{2,6}	{6}	2 {3}		14	24	12
P₃	Diedru hexagonal cantic (prismă triunghiulară)				= h₂{6,2}=t{2,3}				5	9	6
P₆	Diedru hexagonal snub (prismă hexagonală)				s₂{6,2}=t{2,6}				8	18	12
A₃ [2]	Hosoedru hexagonal snub (antiprismă triunghulară), (octaedru)				s{2,6}=sr{2,3}				8	12	6

Operatorii construcției Wythoff

Operația	Simbol	Descriere
Inițial	{p,q} t₀{p,q}	Orice poliedru sau pavare regulate.
Rectificare (r)	r{p,q} t₁{p,q}	Muchiile sunt complet trunchiate în puncte unice. Poliedrul are acum fețele combinate ale poliedrului inițial și ale dualului. Poliedrele sunt denumite prin numărul de laturi ale celor două forme regulate: {p,q} și {q,p}, de exempu „cuboctaedru” pentru r{4,3} între cub și octaedru.
Birectificare (2r) (dual)	2r{p,q} t₂{p,q}	Birectificarea (dualul) este o altă trunchiere, astfel încât fețele originale sunt reduse la puncte. Fețele noi sunt formate sub fiecare vârf al poliedrului ințial. Numărul muchiilor este neschimbat și se rotește cu 90 de grade. O birectificare poate fi văzută ca un dual.
Trunchiere (t)	t{p,q} t_0,1{p,q}	Fiecare vârf original este tăiat, cu o față nouă care umple golul. Trunchierea are un grad de libertate, care are o poziție în care se creează un poliedru uniform trunchiat. Poliedrul are fețele sale originale dublate ca număr de laturi și conține fețele dualului.
Bitrunchiere (2t) (dual trunchiat)	2t{p,q} t_1,2{p,q}	O bitrunchiere poate fi văzută ca trunchierea dualului. Un cub bitruncat este un octaedru trunchiat.
Cantelare (rr) (expandare)	rr{p,q}	În plus față de trunchierea vârfurilor, fiecare muchie originală este teșită, cu fețe dreptunghiulare noi care apar în locul lor. O cantelare uniformă este la jumătatea distanței dintre formele părinte și cele duale. Un poliedru cantelat este numit ca rombi-r{p,q}, de exemplu rombicuboctaedru pentru rr{4,3}.
Cantitrunchiere (tr) (omnitrunchiere)	tr{p,q} t_0,1,2{p,q}	Trunchierea și operațiile de cantelare sunt aplicate împreună pentru a crea o formă omnitrunchiată care are fețele poliedrului inițial dublate în numărul de laturi, fețele dualului dublate în numărul de laturi și pătrate undele existau laturile inițiale.

Operații de alternare
Operația	Simbol	Descriere
Rectificare snub (sr)	sr{p,q}	Cantitrunchiere alternată. Toate fețele originale au la sfârșit jumătate din numărul de laturi, iar pătratele degenerează în muchii. Deoarece formele omnitrunchiate au 3 fețe/vârf, se formează noi triunghiuri. De obicei, aceste forme fațetate alternativ sunt ușor deformate după aceea pentru a se obține din nou poliedre uniforme. Posibilitatea ultimei schimbări depinde de gradul de libertate.
Snub (s)	s{p,2q}	Trunchiere alternată.
Snub cantic (s₂)	s₂{p,2q}
Cantelare alternată (hrr)	hrr{2p,2q}	Posibilă doar la pavări uniforme (poliedre infinite), alternarea De exemplu,
Înjumătățire (h)	h{2p,q}	Alternare a , aceeași cu
Cantic (h₂)	h₂{2p,q}	Aceeași cu
Înjumătățire rectificată (hr)	hr{2p,2q}	Posibilă doar la pavări uniforme (poliedre infinite), alternarea , aceeași cu or De exemplu, = sau
Sfertuire (q)	q{2p,2q}	Posibilă doar la pavări uniforme (poliedre infinite), aceeași cu De exemplu, = or

Note

^ Coxeter, Regular Polytopes, p. 13
^ en Piero della Francesca's Polyhedra, georgehart.com, accesat 2021-02-19
^ en „Stéréo-Club Français - Galerie : Polyedres”. Arhivat din original la 9 octombrie 2016. Accesat în 19 februarie 2021.
^ en Har'El, Z. Uniform Solution for Uniform Polyhedra., Geometriae Dedicata 47, 57-110, 1993. Zvi Har’El, Kaleido software, Images, dual images
^ en Mäder, R. E. Uniform Polyhedra. Mathematica J. 3, 48-57, 1993. [1]
^ Closed-Form Expressions for Uniform Polyhedra and Their Duals, Peter W. Messer, Discrete Comput Geom 27:353–375 (2002)^{[nefuncțională]} (arhivă)

Bibliografie

de Brückner, M. Vielecke und vielflache. Theorie und geschichte.. Leipzig, Germany: Teubner, 1900. [2]
en Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954). „Uniform polyhedra” (PDF). Philosophical Transactions of the Royal Society A. 246 (916): 401–450. doi:10.1098/rsta.1954.0003. ISSN 0080-4614. JSTOR 91532. MR 0062446.
en Grünbaum, B. (1994), „Polyhedra with Hollow Faces”, În Tibor Bisztriczky; Peter McMullen; Rolf Schneider; et al., Proceedings of the NATO Advanced Study Institute on Polytopes: Abstract, Convex and Computational, Springer, pp. 43–70, doi:10.1007/978-94-011-0924-6_3, ISBN 978-94-010-4398-4
en McMullen, Peter; Schulte, Egon (2002), Abstract Regular Polytopes, Cambride University Press
en Skilling, J. (1975). „The complete set of uniform polyhedra”. Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. 278 (1278): 111–135. doi:10.1098/rsta.1975.0022. ISSN 0080-4614. JSTOR 74475. MR 0365333.
en Sopov, S. P. (1970). „A proof of the completeness on the list of elementary homogeneous polyhedra”. Ukrainskiui Geometricheskiui Sbornik (8): 139–156. MR 0326550.
en Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 978-0-521-09859-5.

Vezi și

Lista poliedrelor uniforme

Legături externe

Materiale media legate de poliedru uniform la Wikimedia Commons
en Eric W. Weisstein, Uniform Polyhedron la MathWorld.
en Uniform Solution for Uniform Polyhedra
en The Uniform Polyhedra
en Virtual Polyhedra Uniform Polyhedra
en Uniform polyhedron gallery Arhivat în 9 octombrie 2016, la Wayback Machine.
en Uniform Polyhedron -- from Wolfram MathWorld Has a visual chart of all 75

Portal matematică

v • d • m Politopuri regulate și uniforme convexe fundamentale în dimensiunile 2–10
Familie	A_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
Poligoane regulate	Triunghi	Pătrat	p-gon	Hexagon	Pentagon
Poliedre uniforme	Tetraedru	Octaedru • Cub	Semicub		Dodecaedru • Icosaedru
4-politopuri uniforme	5-celule	16-celule • Tesseract	Semitesseract	24-celule	120-celule • 600-celule
5-politopuri uniforme	5-simplex	5-ortoplex • 5-cub	5-semicub
6-politopuri uniforme	6-simplex	6-ortoplex • 6-cub	6-semicub	1₂₂ • 2₂₁
7-politopuri uniforme	7-simplex	7-ortoplex • 7-cub	7-semicub	1₃₂ • 2₃₁ • 3₂₁
8-politopuri uniforme	8-simplex	8-ortoplex • 8-cub	8-semicub	1₄₂ • 2₄₁ • 4₂₁
9-politopuri uniforme	9-simplex	9-ortoplex • 9-cub	9-semicub
10-politopuri uniforme	10-simplex	10-ortoplex • 10-cub	10-semicub
n-politopuri uniforme	n-simplex	n-ortoplex • n-cub	n-semicub	1_k2 • 2_k1 • k₂₁	n-politop pentagonal
Topicuri: Familii de politopuri • Politop regulat

[1] Coxeter, Regular Polytopes, p. 13

[2] Piero della Francesca's Polyhedra, georgehart.com, accesat 2021-02-19

[3] „Stéréo-Club Français - Galerie : Polyedres”. Arhivat din original la 9 octombrie 2016. Accesat în 19 februarie 2021.

[4] Har'El, Z. Uniform Solution for Uniform Polyhedra., Geometriae Dedicata 47, 57-110, 1993. Zvi Har’El, Kaleido software, Images, dual images

[5] Mäder, R. E. Uniform Polyhedra. Mathematica J. 3, 48-57, 1993. [1]

[6] Closed-Form Expressions for Uniform Polyhedra and Their Duals, Peter W. Messer, Discrete Comput Geom 27:353–375 (2002)^{[nefuncțională]} (arhivă)

[1]