Paralelism (geometrie)

Acest articol sau această secțiune are bibliografia incompletă sau inexistentă. Puteți contribui prin adăugarea de referințe în vederea susținerii bibliografice a afirmațiilor pe care le conține.

În geometrie, paralelismul se referă la o proprietate relațională, în cadrul unui spațiu euclidian, a două sau mai multe subspații (de exemplu drepte sau plane). Presupusa existență și proprietățile dreptelor paralele formează baza axiomei paralelelor a lui Euclid. Două drepte într-un plan care nu se pot intersecta se numesc drepte paralele. Analog, într-un spațiu tridimensional, o dreaptă și un plan sau două plane pot fi paralele; în general, într-un spațiu euclidian n-dimensional, un spațiu m-dimensional și un spațiu n−1-dimensional (cu ${\displaystyle m\leq n-1}$) sunt paralele dacă nu au vectori în comun.

În spații neeuclidiene, dreptele paralele sunt cele care se intersectează doar la limită la infinit.

Simbolul pentru paralelism este ${\displaystyle \parallel }$ . De exemplu ${\displaystyle AB\parallel CD}$ arată că dreapta AB este paralelă cu dreapta CD.

În setul de caractere Unicode, semnele „paralel” și „neparalel” sunt alocate codurilor U+2225 (∥) și respectiv U+2226 (∦).

Date fiind dreptele l și m, următoarele descrieri pentru m o definesc echivalent ca paralelă la dreapta l într-un spațiu euclidian:

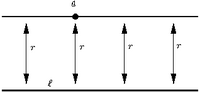
1. Toate punctele de pe dreapta m se află la exact aceeași distanță minimă de dreapta l (drepte echidistante).
2. Dreapta m se află în același plan ca dreapta l dar nu se intersectează cu l (chiar și presupunând că dreptele se extind până la infinit în ambele direcții).
3. Dreptele m și l sunt intersectate de o a treia dreaptă (o secantă) din același plan, iar unghiurile corespunzătoare intersecției cu secanta sunt egale. (Această afirmație este echivalentă cu axioma paralelelor a lui Euclid.)

Cu alte cuvinte, dreptele paralele trebuie să se afle în același plan, iar planele paralele trebuie să se afle în același spațiu tridimensional. O dreaptă poate fi paralelă cu un plan în același spațiu tridimensional.

Cele trei definiții de mai sus duc la trei metode diferite de construire a dreptelor paralele.

• 
  Definiţia 1: Dreapta m are aceeaşi distanţă faţă de dreapta l.
• 
  Definiţia 2: Se ia o dreaptă oarecare prin a care intersectează l în x. Se duce punctul x la infinit.
• 
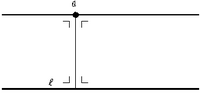
  Definiţia 3: Atât l cât şi m au o aceeaşi secantă prin a care le intersectează la 90°.

O altă definiție a dreptelor paralele utilizată frecvent este aceea că două drepte sunt paralele dacă nu se intersectează, dar aceasta este valabilă doar într-un spațiu bidimensional.

Întrucât o dreaptă paralelă este o dreaptă formată din puncte aflate la aceeași distanță față de cealaltă, atunci există o unică distanță între cele două drepte paralele. Date fiind ecuațiile a două drepte paralele neverticale:

${\displaystyle y=mx+b_{1}\,}$

${\displaystyle y=mx+b_{2}\,}$

distanța între cele două drepte se poate găsi rezolvând sistemul de ecuații liniare:

${\displaystyle y=mx+b_{1}\,}$

${\displaystyle y=-x/m\,}$

și sistemul:

${\displaystyle y=mx+b_{2}\,}$

${\displaystyle y={\frac {-x}{m}}\,}$

pentru a obține coordonatele picioarelor unei perpendiculare pe cele două drepte. Soluția sistemelor este:

${\displaystyle x_{1}\ ={\frac {-b_{1}m}{m^{2}+1}}\,}$

${\displaystyle y_{1}\ ={\frac {b_{1}}{m^{2}+1}}\,}$

${\displaystyle x_{2}\ ={\frac {-b_{2}m}{m^{2}+1}}\,}$

${\displaystyle y_{2}\ ={\frac {b_{2}}{m^{2}+1}}\,}$

Introducând în formula distanței euclidiene rezultă:

${\displaystyle d={\sqrt {\left({\frac {b_{1}m-b_{2}m}{m^{2}+1}}\right)^{2}+\left({\frac {b_{2}-b_{1}}{m^{2}+1}}\right)^{2}}}\,}$

...

${\displaystyle d={\sqrt {\frac {(b_{2}-b_{1})^{2}}{m^{2}+1}}}\,}$

${\displaystyle d={\frac {|b_{2}-b_{1}|}{\sqrt {m^{2}+1}}}\,}$

adică:

${\displaystyle d={\frac {|b_{2}-b_{1}|}{m^{2}+1}}{\sqrt {m^{2}+1}}.}$

De asemenea, dacă cele două drepte sunt

${\displaystyle ax+by+c_{1}=0\,}$

${\displaystyle ax+by+c_{2}=0\,}$

atunci distanța între ele poate fi formulată astfel:

${\displaystyle d={\frac {|c_{2}-c_{1}|}{\sqrt {a^{2}+b^{2}}}}.}$

• Construcția unei linii paralele cu o paralelă dată, printr-un punct exterior (dat sau oarecare) acesteia, utilizând un compas și un liniar — la [Math Open References