Frontalny automat komórkowy

Frontalny automat komórkowy (FCA) – rodzaj algorytmu obliczeń oparty na modelach automatów komórkowych (CA).

Nazwa „frontalny” pochodzi od jednego z najbardziej rozpowszechnionych zastosowań, a mianowicie rozrostu ziaren, kiedy granica rosnącego ziarna jest rozpatrywana jako front zachodzących zmian w strukturze. Podstawową cechą frontalnych automatów jest odwrócenie strumienia informacji w komórce i jako skutek tego wykorzystanie do obliczeń w jednym kroku czasowym tylko części komórek.

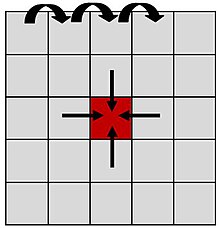
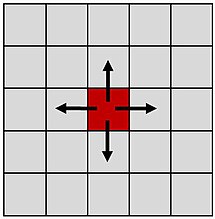
Głównym elementem automatu komórkowego jest określenie stanu komórki, który zapisywany jest poprzez tak zwane reguły przejścia. Reguły te określają stan komórki w kolejnym kroku czasowym na podstawie stanu komórek w jej otoczeniu (może być uwzględniony również bieżący stan tej komórki). Z tego powstaje klasyczny algorytm automatów komórkowych, gdy komórka zbiera informacje ze swojego otoczenia. Przykład prezentuje rysunek 1a. Komórka w środku rysunku jest komórką, dla której sprawdzane są reguły przejścia i otrzymuje ona z sąsiednich komórek (przykład dla otoczenia von Neumanna) informacje o ich stanach. W wyniku tego dla zrealizowania jednego kroku czasowego należy po kolei (strzałki na górze rysunku) zbadać całą przestrzeń pod względem sprawdzenia reguły przejścia, przy czym dla każdej komórki jest badane całe jej otoczenie. We frontalnym automacie komórkowym kierunek przekazywania informacji jest odwrócony, jak pokazano na rysunku 1b. Jest to pierwszy krok, który nie daje jeszcze żadnych korzyści, ponieważ również w tym przypadku należy przejść po całej przestrzeni i nie ma różnicy, czy komórka będzie zbierała informację, czy ją rozsyłała.

a)		b)
	Rys. 1

Różnica między tymi algorytmami powstaje, jeżeli będziemy rozpatrywać stany ustalone i przejściowe. Jeżeli w otoczeniu komórki nie zachodzą żadne zmiany, pozostaje ona w tym samym stanie bez zmian i można mówić, że znajduje się w stanie ustalonym. Odwrotnie, jeżeli w otoczeniu komórki następują zmiany i spowoduje to zmianę jej stanu, będzie ona w stanie przejściowym. Już w tym momencie pojawiają się różnice między tymi dwoma algorytmami, ponieważ przy zbieraniu informacji z otoczenia nie powstają żadne okoliczności wskazujące na to czy zbierać taką informację, czy też nie. Natomiast przy rozprowadzaniu informacji od komórki jest to podstawą do podjęcia tej czy innej decyzji. Komórka, która nie zmienia swego stanu, nie będzie wysyłała żadnej informacji do swego otoczenia natomiast, gdy nastąpią zmiany w jej stanie, komórki w całym otoczeniu otrzymają taką wiadomość i na jej podstawie sprawdzą reguły przejścia, nie badając swego otoczenia. To jest drugi krok.

Trzeci, a zarazem ostatni krok polega na wykorzystaniu do obliczeń tylko komórek w stanie przejściowym. Jeżeli drugi krok polegał na wysyłaniu sygnałów tylko od komórek w stanie przejściowym, ale pozostawieniu badania całej przestrzeni, to istotą trzeciego kroku modernizacji algorytmu jest ograniczenie badania przestrzeni wyłącznie do komórek w stanie przejściowym.

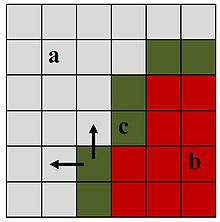
Jako przykład skutecznego zastosowania można rozpatrywać proces rozrostu ziaren. Fragment przestrzeni z rosnącym ziarnem pokazano na rysunku 2. W dowolnym procesie rozrostu kryształu lub ziarna, można wyróżnić trzy strefy. W pierwszej strefie (a) nie następują jeszcze żadne zmiany stanu początkowego. W drugiej strefie (b) takie zmiany już nastąpiły i dalsze zmiany już nie zajdą. Ostatecznie, w trzeciej strefie (c) zachodzą natomiast zmiany w rozpatrywanej chwili czasu i dlatego też, tylko ta trzecia strefa może być wykorzystana w obliczeniach. Zarówno pierwsza, jak i druga strefa, powinny być wyłączone z obliczeń w bieżącym kroku, ponieważ zmiany stanu komórek w nich nie są oczekiwane i nie mogą nastąpić. Dla zaznaczonej na rysunku 2 komórki w stanie przejściowym pokazano strzałkami przekazanie istotnej informacji do jej otoczenia. Więc w bieżącym kroku tylko 6 komórek w strefie (c) będzie uczestniczyć w obliczeniach.

Rys. 2

Wykorzystanie FCA, zamiast konwencjonalnych automatów komórkowych, daje możliwość redukcji czasu obliczeń w modelu 2D, ale jest szczególnie widoczne w 3D CA, ponieważ istotne obszary przestrzeni są wyłączone z obliczeń w każdym kroku czasowym i tylko cienka warstwa uczestniczy w obliczeniach. W klasycznych CA każdy krok wymaga praktycznie tych samych nakładów i czas jego wyznaczenia w ciągu całej symulacji pozostaje bez zmian. Natomiast czas obliczeń w jednym kroku FCA zależy od liczby uczestniczących w obliczeniach komórek i zmienia się w szerokim zakresie, zawsze pozostając małym ułamkiem w porównaniu do czasu obliczeń jednego kroku w klasycznych CA. Każda komórka FCA faktycznie uczestniczy w obliczeniach jednokrotnie w całym procesie obliczeń, natomiast w klasycznym algorytmie w każdym kroku czasowym.

Przykłady oszacowań nakładów obliczeniowych dla kilku prostych wariantów.

Wariant pierwszy: przestrzeń dwuwymiarowa 100×100 komórek, jeden zarodek. Obliczenia do wypełnienia całej przestrzeni z sąsiedztwem von Neumanna (4 sąsiadów) bez opóźnienia.

Wariant drugi: przestrzeń trójwymiarowa 100×100×100 komórek, jeden zarodek. Obliczenia do wypełnienia całej przestrzeni z sąsiedztwem Moore’a (26 sąsiadów) ziarno rośnie w kształcie kuli ze średnim opóźnieniem przejścia równym 3.

Nakłady różnią się o kilka rzędów. Im większa liczba cykli, tym większa różnica (tablica).

	Klasyczny algorytm		Frontalny automat		Stosunek klasycznego do frontalnego
	War. 1	War. 2	War. 1	War. 2	War. 1	War. 2
Liczba cykli od zarodkowania do wypełnienia całej przestrzeni	50	184	50	184	1	1
Liczba badanych komórek we wszystkich cyklach	5 · 10⁵	1,84 · 10⁸	10⁴	3 · 10⁶	50	61
Liczba międzykomórkowej komunikacji we wszystkich cyklach	2 · 10⁶	4,78 · 10⁹	4 · 10⁴	2,6 · 10⁷	50	184

Bibliografia

Linki zewnętrzne

http://home.agh.edu.pl/~lach