トロミノ

トロミノまたはトリオミノは位数3のポリオミノである。3個の同じ大きさの正方形を辺に沿ってつなげると、2種類の形ができる。これらの総称をトロミノという。
トロミノの数
[編集]トロミノは上にあげた2種類が存在する。呼び方は何通りかあるが、本稿では左のものをI型、右のものをL型とする。
この2片は共に線対称形なので片面型トロミノも2種類である。I型は180度回転対称だが、L型は回転対称でない。よって、回転角度が90度の倍数のとき、片面有向トロミノは6種類である[1]。
トロミノの問題
[編集]ポリオミノで一般的な「セット全てを1度ずつ使用して形を作る」という問題は、片数が少ないために出題されない。
長方形を作る
[編集]片面有向トロミノ6種類で長方形を作ることは可能である。また、トロミノ2セットを使用して3×4や2×6の長方形を作ることができる。
1種類の片を複数使用して長方形を作るという問題は、I型の場合は自明である。L型も2片で2×3の長方形ができるので簡単である。芦ヶ原伸之はこの2×3の長方形の使用を禁じた問題を出題している[2]。
L型トロミノの分割
[編集]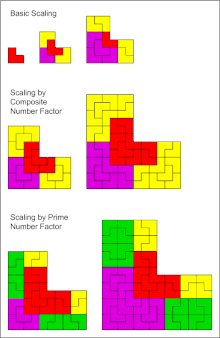
L型トロミノを合同な4つの図形に分割するという問題がある。この問題では出題時に形の条件は与えられていないが、1辺が半分のL型トロミノに分割することができる。
この4片を同様に分割することによって、4n片の合同なL型トロミノに分割することができる。左の図で明らかな通り、一般に任意の n に対して n2片の合同分割が可能である。
チェス盤充填
[編集]同じ種類のトロミノをチェス盤に置くことを考える。チェス盤は 8×8=64 マスなので、21片置くと1マス余る。
I型トロミノを置く場合、空所の位置は限定される。この空所の位置を求める問題は、ハンガリーの数学コンテストで出題されたことがある。
L型トロミノをおく場合、空所はどこにあっても問題がない。実際には 2n×2n のマス目から任意の1マスを除いた図形はL型トロミノ��埋めることができることは帰納法により証明が可能である。

