אפיציקלואיד

בגאומטריה, אפיציקלואיד הוא עקומה הנוצרת על ידי התחקות אחר הנתיב של נקודה נבחרת על היקף מעגל – המכונה "אפיציקל" – שמתגלגל סביב מעגל קבוע על היקפו. זהו סוג מסוים של רולטה.

אם למעגל הקטן יש רדיוס r, ולמעגל הגדול יש רדיוס R, אזי ניתן לבטא את העקומה על ידי המשוואות הפרמטריות הבאות:

${\displaystyle x(\theta )=(R+r)\cos \theta \ -r\cos \left({\frac {R+r}{r}}\theta \right)}$

${\displaystyle y(\theta )=(R+r)\sin \theta \ -r\sin \left({\frac {R+r}{r}}\theta \right),}$

או, אם נסמן k=R/r:

${\displaystyle x(\theta )=r(k+1)\cos \theta -r\cos \left((k+1)\theta \right)\,}$

${\displaystyle y(\theta )=r(k+1)\sin \theta -r\sin \left((k+1)\theta \right).\,}$

או, בהצגה במישור המרוכב^[1]:

${\displaystyle z(\theta )=r(e^{i(k+1)\theta }-(k+1)e^{i\theta })}$

כאשר בכל הנוסחאות, ${\displaystyle \theta \in [0,2\pi ]}$.

אם k, היחס בין הרדיוס של המעגל הקבוע לרדיוס המעגל שמסתובב עליו, הוא מספר שלם חיובי, אז השטח של האפיציקלואיד הוא

${\displaystyle A=(k+1)(k+2)\pi r^{2}.}$

במקרה זה, העקומה סגורה, פשוטה, ויש לה k פינות חדות.

אם k הוא מספר רציונלי שניתן לכתיבה כשבר מצומצם כ-k=p/q עם q>1, אז העקומה סגורה, אינה פשוטה ויש לה p פינות. המעגל המסתובב מקיף את המעגל הקבוע q פעמים עד שהעקומה נסגרת.

אם k הוא מספר אי-רציונלי, העקומה לעולם לא תחזור על עצמה, והגרף שלה מהווה קבוצה צפופה בשטח שבין המעגל הקבוע (שרדיוסו R) לבין מעגל בעל רדיוס R+2r.

בכל המקרים, המרחק מראשית הצירים אל העקומה משתרע על הטווח שבין R ל- R+2r.

• דוגמאות לאפיציקלואידים
• 
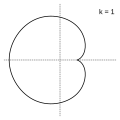
  k = 1: קרדיואידה
• 
  k = 2: נפרואידה
• 
  k = 3: טרפולואידה
• 
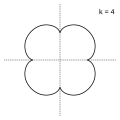
  k = 4: קוואטרפולואידה
• 
  k = 2.1 = 21/10
• 
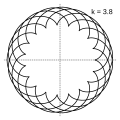
  k = 3.8 = 19/5
• 
  k = 5.5 = 11/2
• 
  k = 7.2 = 36/5

האפיציקלואיד הוא מקרה מיוחד של האפיטרוכואיד.

אפיציקלואיד עם פינה אחת נקרא קרדיואידה, ועם שתי פינות - נפרואידה.

האפיציקלואיד והאבולוט שלו דומים זה לזה.

• ציקלואידה
• אפיטרוכואיד
• היפוטרוכואיד
• קבוצת מולטיברוט

מדיה וקבצים בנושא אפיציקלואיד בוויקישיתוף

• אפיציקלואיד, באתר MathWorld (באנגלית)