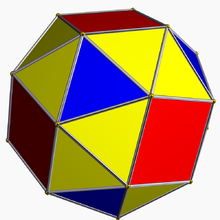
Cube adouci

Cube adouci

Éléments

Faces	Arêtes	Sommets
38 triangles et carrés	60	24 de degré 5

Données clés

Type	Solide d'Archimède
Caractéristique	2
Propriétés	Semi-régulier et convexe, chiral
Volume (arête a)	${\displaystyle {\frac {{\sqrt {2\tau }}(7\tau ^{2}+1)}{6}}a^{3}}$ où ${\displaystyle \tau }$ est la constante de Tribonacci
Aire de surface	${\displaystyle (6+8{\sqrt {3}})a^{2}}$
Groupe de symétrie	O
Dual	Icositétraèdre pentagonal

modifier

Le cube adouci, ou cube camus^[1], ou encore snub cube est un solide d'Archimède.

Le cube adouci possède 38 faces dont 6 sont des carrés et les 32 autres sont des triangles équilatéraux. Il possède 60 arêtes et 24 sommets. Il a deux formes distinctes, qui sont leurs images dans un miroir (ou "énantiomorphes") l'un de l'autre.

Étant obtenu par adoucissement (en) du cube et de l'octaèdre, il est aussi appelé cuboctaèdre adouci.

Les coordonnées cartésiennes des sommets du cube adouci sont les permutations paires de ${\displaystyle \left(\pm 1,\pm \tau ,\pm {\frac {1}{\tau }}\right)\,}$avec un nombre pair de signes plus, et les permutations impaires avec un nombre impair de signes plus, où ξ est la constante de Tribonacci, solution réelle de

${\displaystyle \tau ^{3}=\tau ^{2}+\tau +1\,}$,

et qui peut s'écrire

${\displaystyle \tau ={\frac {{\sqrt[{3}]{19+3{\sqrt {33}}}}+{\sqrt[{3}]{19-3{\sqrt {33}}}}+1}{3}}\simeq 1,8392867552}$

En prenant les permutations paires avec un nombre impair de signes plus, et les permutations impaires avec un nombre pair de signes plus, on obtient un cube adouci différent, l'image miroir.

La longueur des arêtes de ce cube adouci est ${\displaystyle a={\frac {\sqrt {2(1+\tau ^{2})}}{\tau }}}$.

Parmi les 6 permutations de 3 coordonnées, les permutations paires sont les 3 permutations circulaires.

Le cube adouci peut être engendré^[2] en prenant les six faces d'un cube de côté de longueur a, en les translatant d'une longueur ${\displaystyle d=\left(-{\frac {1}{2}}+{\sqrt {\frac {\tau -1}{4(2-\tau )}}}\right)\times a}$ vers l'extérieur de façon qu'elles ne se touchent plus. Puis, on leur donne une rotation autour de leur centre (toutes dans le sens horaire ou toutes dans le sens antihoraire relativement à l'axe orthogonal à leur face et sortant du cube) d'un angle ${\displaystyle \theta =\arccos \left({\sqrt {\frac {\tau }{2}}}\right)=\arctan \left({\frac {\tau -1}{\tau +1}}\right)}$, de sorte que les espaces entre les faces carrées puissent être remplis par des triangles équilatéraux.

On peut aussi l'obtenir à partir du petit rhombicuboctaèdre en traçant une diagonale dans 12 des 18 carrés que ce polyèdre possède, (à savoir ceux qui ont un côté en commun avec l'un des 8 triangles du rhombicuboctaèdre), puis en déformant les 24 triangles rectangles ainsi obtenus en triangles équilatéraux^[3].

Le cube adouci ne doit pas être confondu avec le cube tronqué.

• Le dodécaèdre adouci
• Polyèdre adouci

• (en) Robert Williams, The Geometrical Foundation of Natural Structure : A Source Book of Design, 1979, 265 p. (ISBN 0-486-23729-X).

• (en) Les polyèdres uniformes
• (en) Les polyèdres en réalité virtuelle dans l'encyclopédie des polyèdres
• Cube adouci dans MathCurve.

• Portail de la géométrie