كتاب في الأصول الهندسية/الكتاب الأول
الكتاب الأول
إيضاح الاصطلاحات والعلامات
١ الهندسة علمُ موضوعه قياس المقادير. والمقدار هو كل ما لهُ واحدٌ من ثلاثة أشياء وهي طولٌ وعرضٌ وعمقٌ
٢ قد استعملت في علم الهندسة اصطلاحاتٌ شتَّى كالحد والقضية والأوليَّة والنظريَّة والعمليَّة والسابقة والتعليقة والفرع وغير ذلك مما سترى
٣ الح�� هو إيضاح معنى لفظة اصطلاحيَّة. ويجب أن تكون تامَّا لا أشكال فيه وأن تكون ألفاظهُ المفردة اعتياديَّة مفهومة
٤ الأوليَّة قضية واضحة لا تقبل زيادة إيضاح كقولهم الكل أعظم من جزءه
٥ النظرية قضيَّة محتاجة إلى برهان لإثبات صحتها كقولهم أن الزوايا الثلاث من كل مثلث تعدل قائمتين
٦ البرهان المستقيم هو ما أثبت صحة قضية ويُسَمَّى أيضاً البرهان الإيجابي
٧ البرهان الغير المستقيم هو ما أثبت صحة قضية بإثبات محاليَّة فسادها، ويسمى أيضاً البرهان السلبي والتحويل إلى المحال
٨ العمليَّة هي قضية حاوية عملاً مطلوباً إتمامهُ كقولهم علينا أن نرسم خطَّاً عموداً على آخر وأن نقسم عدداً إلى اجزاء مفروضة
٩ حلُّ عمليَّةٍ هو استخراج جوابها. فإن عُبّر عن ذلك بإعدادٍ سُمّي حلاً عددياً أو بمبادئ هندسيّة فهندسيَّاً. وان تم بواسطة امتحانات فميكانكيَّاً أو صناعيَّاً
١٠ السابقة قضية استعدادية ذُكِرَت قبل أخرى لكي يُختَصَر بها برهان الاخرى ١١ الفرع نتيجة تُستنتج بالاستقامة من قضية سابقة لها
١٢ التعليقة قول مبنى على قضيَّة سبقته
١٣ الافتراض هو أن يسلم بصحة قضية لكي يبنى عليها برهان قضية اخرى
١٤ المقتضيات أو الممكنات عملياتٌ يسلّم بإمكان عملها من أول وهلةٍ
١٥ النظام هو صناعة وضع جملة براهين متتابعة على ترتيب مناسب للبحث عن صحة قضية أو فسادها أو لبرهانها للغير
١٦ التحليل هو استعلام صحة قضية بالتأخر من القضية نفسها إلى مبدإِ معلوم ويسمى أيضاً النظام التحليلي وهو المستعمل في علم الجبر والمقابلة
١٧ التركيب هو التقدم شيئاً فشيئاً من مبدإ معلوم إلى النتيجة ويسمى أيضاً النظام التركيبي وهو المستعمل في علم الهندسة
١٨ العلامات المستعملة في هذا الكتاب قد تقدم شرحها في كتاب علم الجبر والمقابلة فعليك بالمراجعة
حدود
١ النقطة شيءٌ لهُ وضع فقط وليس لهُ طول ولا عرض ولا عمق
٢ الخط طولٌ بدون عرض أو عمق
فرعٌ: نهايتا خطٍ نقطتان وموضع تقاطع خطَّين نقطة
٣ خطَّان لا يتوافقان في نقطتين منهما بدون أن يتوافقا بالكليَّة يسميان مستقيمين. وقيل أيضاً الخط المستقيم هو البعد الاقرب بين نقطتين
فرعٌ: خطان مستقيمان لا يحيطان بمساحةٍ ولا يتطابقان في جزء منهما أن لم يتطابقا بالكليَّة
٤ السطح أو البسيط ما كان لهُ طول وعرض بدون عمق فرعُ. نهايات سطحٍ خطوطٌ. وموضع تقاطع سطحين خطٌ ٥ السطح المستوي هو سطحٌ إذا فُرِضَت فيهِ نقطتان فالخط المستقيم الموصل بينهما يقع جميعه في ذلك السطح
٦ الزاوية المستقيمة البسيطة هي انفراج خطَّين مستقيمين التقيا بنقطةٍ وليسا على استقامةٍ واحدةٍ
تنبيهٌ: متى التقت زاويتان فأكثر في نقطة واحدةٍ كما يرى عند ب فكل واحدة منها تتعين بثلاثة احرفٍ اوسطها عند رأس الزاوية. فالزاوية الواقعة بين خط ا ب وخط د ب تسمى زاوية ا ب د أو د ب ا والواقعة بين د ب و س ب تسمى د ب س أو س ب د وأما الزاوية المفردة فيدَلُّ عليها بحرف واحد كالزاوية عند ي
٧ إذا قام خطٌ مستقيم على آخر مستقيم وأحدث زاويتين متساويتين على جانبيهِ فالخط القائم يسمى عموداً وكل زاويةٍ منهما قائمة
۸ الزاوية المنفرجة هي كل زاوية أكبر من قائمة
۹ الزاوية الحادَّة هي كل زاوية أصغر من قائمة
۱۰ الشكل هيئةٌ محدودة. ومساحة الشكل هي الفسيحة المنحصرة في حدوده بدون نظر إلى ماهيّة تلك الحدود
۱۱ الدائرة شكل مستو يحيط بهِ خط واحد ويسمى المحيط. وفي وسطهِ نقطةٌ جميع الخطوط المستقيمة الخارجة منها إلى المحيط متساوية
۱۲ النقطة المشار إليها تسمى مركز الدائرة
۱۳ قُطْرُ الدائرة خط مستقيم مارٌّ بمركزها ونهايتاه في محيطها
۱٤ نصف الدائرة هو الشكل المحاط بالقطر والجزء من المحيط المقطوع بالقطر
۱٥ الأشكال المستقيمة الأضلاع هي المحدودة بخطوط مستقيمة
۱٦ المثلث شكل يحيط به ثلاثة خطوط
تنبيه: المثلث المستوى هو ما أحـاط بهِ ثلاثة خطوط مستقيمة والكروي ما أحـاط بهِ ثلاثة خطوط منحنية
۱٧ ذو الأربعة الأضلاع شكل احـاط بهِ أكثر من أربعة خطوط مستقيمة
۱۸ الشكل الكثير الأضلاع ما احاط بهِ أكثر من أربعة خطوط مستقيمة
۱۹ المثلث المتساوي الأضلاع هو ما كانت أضلاعه الثلاثة متساوية

۲۰ المثلث المتساوي الساقين هو ما كان ضلعان من أضلاعهِ الثلاثة متساويين

۲۱ المثلث المختلف الأضلاع هو ما كانت أضلاعه الثلاثة غير متساوية

۲۲ المثلث القائم الزاوية هو ما كانت إحدى زواياه قائمة

۲۳ المثلث المتفرج الزاوية هو ما كانت إحدى زواياه منفرجة
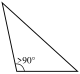
۲٤ المثلث الحاد الزاوية هو ما كانت زواياهُ الثلاث حادًّة

۲٥ المربع شكل يحيط بهِ أربعة خطوط مستقيمة متساوية وكل زواياهُ قائمة

۲٦ المستطيل هو ما كانت كل زواياهُ قائمة ولكن ليس كل أضلاعه متساوية

۲٧ المعيّن ما كانت أضلاعه متساوية ولكن ليست فيهِ قائمة

۲۸ الشبيه بالمعين ما كان ضلعاه المتقابلان متساويين وليست فيهِ قائمة وأضلاعهُ الأربعة ليست متساوية

۲۹ كل ذي أربعة أضلاع غير ما ذكر يسمى منحرفاً
۳۰ الخطوط المستقيمة المتوازية هي الواقعة في سطح واحد مستوٍ ولا تلتقي ولو أخرجت في جهتيها إلى غير نهاية.
مقتضيات أو ممكنات
۱ يمكن أن يوصل بين كل نقطتين بخط مستقيم أو غير مستقيم.
۲ يمكن أن يخُرَج خطٌ مستقيم محدود على استقامتهِ في جهتيهِ إلى حدّ ما يُراد.
۳ يمكن أن تُرسَم دائرةٌ على أي مركزٍ فُرِض وعلى أي بُعدٍ فُرِض منهُ.
أوليات
۱ الأشياء المساوية لشيءٍ واحدٍ هي متساوية بعضها لبعض.
۲ إذا أضِيفَتْ أشياء متساوية إلى أشياء متساوية تكون المجموعات متساوية.
۳ إذا طُرِحَت أشياء متساوية من أشياء متساوية تكون البقايا متساوية.
٤ إذا أضِيفَتْ أشياء متساوية إلى أشياء غير متساوية تكون المجموعات غير متساوية.
٥ إذا طُرِحَت أشياء متساوية من أشياء غير متساوية تكون البقايا غير متساوية.
٦ الاشياء التي هي مضاعف شيء واحدٍ هي متساوية.
٧ الاشياء التي تعدل نصف شيء واحدٍ هي متساوية.
۸ المقادير المتطابقة أي التي تملا مساحة واحدة هي متساوية. ۹ الكل أعظم من جزءه.
۱۰ جميع الزوايا القائمة متساوية.
۱۱ إذا تقاطع خطًّان مستقيمان لا يكونان موازيين لخطٍ آخر مستقيم.
القضية الأولى.عمليَّة
علينا أن نرسم مثلثاً متساوي الأضلاع على خطٍّ مستقيم محدود مفروض
ليكن ا ب الخط المستقيم المفروض فعلينا أن نرسم عليه مثلثاً متساوي الأضلاع.
أجعل ا مركزاً و ا ب بعداً وارسم دائرة ب س د ثم أجعل ب مركزاً و ب ا بُعداً وارسم دائرة ا س ر (حسب ثالثة الممكنات)
ثم من س أي نقطة تقاطع الدائرتين ارسم خطًّاً إلى ا وآخر إلى ب (حسب أولى الممكنات)
فيكون ا ب س مثلثاً متساوي الأضلاع
فالنقطة ا هي مركز الدائرة ب س د ولذلك ب ا يعدل ب س وقد تبرهن أن ا س يعدل ا ب والاشياء المساوية لشيء واحدٍ هي متساوية بعضها لبعض (أوليَّة أولى)
فلذلك ب س يعدل ا س فالخطوط الثلاثة ا ب، ا س، ب س هي متساوية فيكون ا ب س مثلثاً متساوي الأضلاع وقد رسم على ا ب
وذلك ما كان علينا أن نعمله
القضية الثانية.ع
علينا أن نرسم من نقطة مفروضة خطّاً مستقيماً يعدل خطّاً أخر مستقيماً مفروضاً
لتكن ا النقطة المفروضة و ب س الخط المستقيم المفروض فعلينا أن نرسم من ا خطّاً يعدل ب س.
من النقطة المفروضة ا ارسم الخط ا ب (أولي المقتضيات)
وارسم على ا ب مثلثاً متساوي الأضلاع ا ب د (حسب ق ۱ ك ۱)
ثم أخرج د ب إلى ق و د ا إلى ي (حسب ثانية المقتضيات)
ثم اجعل ب مركزاً و ب س بعداً وارسم دائرة س غ ح (حسب ثالثة المقتضيات)
وأجعل د مركزاً و د غ بعداً وارسم دائرة غ ل ك فالخط ا ل يعدل الخط س النقطة ب هي مركز الدائرة غ س ح ولذلك ب س يعدل ب غ (حد ۱۱)
والنقطة د هي مركز الدائرة غ ك ل ولذلك الخط د ل يعدل د غ والجزء د ا يعدل الجزء د ب فالبقية ا ل تعدل البقية ب غ (أولية ثالثة)
وقد تبرهن أن ب س يعدل ب غ والاشياء المساوية لشيء واحد هي متساوية بعضها لبعض فالخط ا ل يعدل الخط ب س وقد رُسم من ا النقطة المفروضة
وذلك ما كان علينا أن نعملهُ
القضية الثالثة.ع
علينا أن نقطع من أطول خطَّين مستقيمين مفروضين جزءاً يعدل أقصرهما
ليكن ا ب اطول الخطًّين المفروضين و س أقصرهما.
فعلينا أن نقطع من ا ب جزءاً يعدل س (حسب ق ۲ ك ۱)
ثم اجعل ا مركزاً و ا ت بعداً وارسم دائرة ت ي ف (ثالثة المقتضيات)
فالجزءُ أي يعدل ا ت (حد ۱۱)
و ا ت يعدل س فلذلك أي يعدل س (أولية أولى)
وقد قطع من ا ب أطول الخطًّين المفروضين
وذلك ما كان علينا أن نعملهُ
القضية الرابعة. نظريَّة
إذا عدل ضلعا مثلثٍ ضلعَي مثلثٍ آخر والزاوية الواقعة بين ضلعي أحدهما عدلت الواقعة بين ضلعي الآخر فالضلع الثالث من الواحد يعدل الثالث من الآخر ويكون المثلثان متساويين والزاويتان الأخريان من الواحد تعدلان الأخريين من الآخر
ليكن ا ب س، د ي ف مثلثين.
والضلعان ا ب، ا س من الواحد يعدلان د ي، د ف من الآخر كل واحد يعدل نظيرهُ، والزاوية ب ا س تعدل الزاوية ي د ف، فحينئذ القاعدة ب س تعدل القاعدة المثلث ي ف.
والمثلث ا ب س يعدل المثلث د ي ف.
وبقية الزوايا أيضاً متساوية أي التي تقابلها الأضلاع المتساوية كل واحدة تعدل نظيرها.
أي ا ب س تعدل د ي ف و ا س ب تعدل د ف ي
لأنهُ إذا وُضع المثلث ا ب س على المثلث د ي ف حتى تقع النقطة ا على النقطة د، والخط ا ب على الخط د ي فالنقطة ب تقع على النقطة ي لأن ا ب يعدل د ي.
وإذا وقع ا ب على د ي، فحينئذٍ ا س يقع د ف، لأن الزاوية ب ا س تعدل الزاوية ي د ف، والنقطة س تقع على النقطة ف، لأن ا س يعدل د ف.
وقد تبرهن أن النقطة ب تقع على النقطة ي فالقاعدة ب س تقع على القاعدة ي ف وتعدلها (فرع حد ٣)
وكذلك كل المثلث ا ب س يقع على كل المثلث د ي ف ويكونان متساويين.
والزاويتان الأخريان من الواحد تقع على الأخريين من الآخر.
وكل واحدة تعدل نظيرها أي ا ب س تعدل د ي ف و ا س ب تعدل د ف ي.
وذلك ما كان علينا أن نبرهنهُ
القضية الخامسة.ن
في كل مثلث متساوي الساقين الزاويتان عند القاعدة متساويتان. وإذا أخرج الضلعان المتساويان فالزاويتان الحادثتان على الجانب الآخر من القاعدة متساويتان أيضاً
ليكن ا ب س مثلثاً متساوي الساقين أي الساق ا ب يعدل الساق ا س.
وليخرج الضلع ا ب إلى د والضلع ا س إلى ي.
فالزاوية ا ب س تعدل الزاوية ا س ب والزاوية س ب د تعادل الزاوية ب س ي
عين أي نقطة شئت في ب د كالنقطة ق مثلاً.
ومن أي أطول خطين اقطع ا غ حتى يعدل ا ق أقصرهما (حسب ق ۳ ك ۱)
وارسم الخطَّ ق س والخط غ ب.
فالخط ا ق يعدل ا غ وكذلك ا ب يعدل ا س.
فالخطان ق ا، ا س يعدلان غ ا، ا ب، وبينهما الزاوية ق ا غ المشتركة بين المثلثين ا ق س، ا غ ب فالقاعدة ق س تعدل القاعدة غ ب (حسب ق ٤ ك ۱)
والمثلث ا ق س يعدل المثلث ا غ ب فبقية الزوايا من الواحد تعدل نظيرها أي التي تحاذيها الأضلاع المتساوية أي الزاوية ا س ق تعدل ا ب غ والزاوية ا ق س تعدل ا غ ب.
وقد تقدم أن ا ق يعدل ا غ وأن ا ب يعدل ا س فالبقية ب ق تعدل البقية س غ (أولية ثالثة)
وقد تبرهن أن ق س يعدل غ ب فالضلعان ب ق، ق س يعدلان الضلعين س غ، غ ب، وتبرهن أن الزاوية ب ق س تعدل الزاوية س غ ب فالمثلث ب ق س يعدل المثلث س غ ب (ق ٤ ك ۱)
وبقية الزوايا من الواحد تعدل بقية الزوايا من الأخر أي التي تقابلها الأضلاع المتساوية أي الزاوية ق ب س تعدل الزاوية غ س ب والزاوية ب س ق تعدل الزاوية س ب غ، وقد تبرهن أن كل الزاوية ا س ق تعدل الكل ا ب غ، وأن الجزء ب س ق يعدل الجزء س ب غ، فالبقية ا س ب تعدل البقية ا ب س وهما الزاويتان عند قاعدة المثلث ا ب س، وقد تبرهن أن الزاوية ق ب س تعدل غ س ب وهما الزاويتان على الجانب الأخر من القاعدة.
وذلك ما كان علينا ان نبرهنه
فرع: إذ ذاك يكون كل مثلث متساوي الاضلاع متساوي الزوايا أيضاً
القضية السادسة.ن
إذا كانت زاويتان من مثلثٍ متساويتين فالضلعان اللذان يقابلانها هما متساويان أيضاً ليكن ا ب س مثلثاً لهُ زاويتان ا ب س، ا س ب متساويتان فضلعاهُ ا ب، ا س هما متساويان أيضاً
وإلا فأحدهما أطول من الاخر. فلنفرض ا ب أطولهما ولنقطع منهُ جزءاً د ب يعدل ا س أقصرهما (ق ٣ ك ١)
فلنا في المثلثين د ب س، ا ب س ضلعٌ من الوّاحد د ب يعدل ضلعاً من الآخر ا س، والقاعدة ب س مشتركة بينهما فالضلعان د ب، ب س يعدلان ا س، س ب كل واحدٍ نظيرَهُ.
والزاوية د ب س تعدل ا س ب فالقاعدة د س تعدل القاعدة ا ب والمثلث د ب س يعدل المثلث ا ب س (ق ٤ ك ١)
أي الأصغر يعدل الأكبر وذلك محال فلا يمكن ان يكون ا ب، ا س غير متساويين بل هما متساويان.
وذلك ما كان علينا أن نبرهنه
فرعٌ. كل مثلث متساوي الزوايا هو متساوي الأضلاع أيضاً
القضية السابعة.ن
لا يكون على قاعدة واحدة وعلى جانب واحد منها مثلثان الضلعان منهما المنتهيان في طرف واحد من القاعدة متساويان والمنتهيان في طرفها الآخر متساويان أيضاً
ليكن ا س ب، ا د ب مثلثين على قاعدة واحدة ا ب وعلى جانب واحد منهما والضلعان ا س، ا د المنتهيان في ا متساويان المنتهيان في ب الطرف الآخر من القاعدة لا يكونان متساويين
ارسم الخطّ س د (حسب أولى الممكنات)
فإذا كان ب س، ب د متساويين وكان رأس أحد المثلثين خارج الاخر فلنا ا س، ا د متساويان فالزاوية ا س د تعدل الزاوية ا د س (حسب ق ٥ ك ١)
والزاوية ا س د أنما هي أكبر من الزاوية ب س د، فالزاوية ا د س أيضاً أكبر من ب س د، وبالأحرى الزاوية ب د س أكبر من ب س د وعلى ما فُرِض أن س ب يعدل د ب فالزاوية ب د س تعدل ب س د (ق ٥ ك ١) وقد تبرهن أنها أكبر ب س د
ثم إذا وقع رأس أحد المثلثين مثل د داخل الآخر ا س ب.
فاخرج ا س إلى ي واخرج ا د إلى ق فيما أن ا س، ا د متساويان فالزاويتان ي س د، ق د س على الجانب الآخر من القاعدة س د هما متساويتان (ق ٥ ك ١)
والزاوية ي س د إنما هي أكبر من الزاوية ب س د فالزاوية ق د س أيضاً أكبر من ب س د وبالأحرى ب د س أكبر من ب س د وإذا كان ب د، ب س متساويين فالزاوية ب د س تعدل الزاوية ب س د (ق ٥ ك ١)
وقد تبرهن أن ب د س أكبر من ب س د وذاك محال.
وهكذا إذا وقع رأس أحد المثلثين بجانب الآخر فلا يمكن أن يكون على قاعدة واحدة وعلى جانب واحد منها مثلثان الضلعان منهما المنتهيان إلى طرف واحد من القاعدة متساوين والمنتهيان إلى طرفها الآخر متساويان أيضاً
القضية الثامنة.ن
إذا عدل ضلعا مثلثٍ ضلعي مثلثٍ آخر وكانت القاعدتان متساويتين أيضاً فالزاوية الحادثة بين ضلعي الواحد تعدل الحادثة بين ضلعي الآخر
ليكن ا ب س، د ي ف مثلثين والضلعان ا ب، ا س يعدلان د ي، د ف كل واحد يعدل نظيره.
والقاعدة ب س تعدل القاعدة ي ف فالزاوية ب ا س تعدل الزاوية ي د ف
لأنهُ إذا وضع المثلث ا ب س على المثلث د ي ف حتى تقع النقطة ب على والنقطة ي والخطّ ب س على الخطّ ي ف فالنقطة س تقع على النقطة ف لأن الخط ب س يعدل ي ف وإذ ذاك فالخط ب ا يقع على الخط ي د والخط ا س يقع على د ف، وإلا فلنفرض وقوعهما على ي ر، ر ف فعندها ذلك يكون على قاعدة واحدة وعلى جانبٍ واحدٍ منها مثلثان الضلعان منهما المنتهيان في طرف واحد من القاعدة متساويان والمنتهيان في طرفها الآخر متساويان أيضاً وذلك لا يمكن (ق ٧ ك ١)
فإذا طبق ب س على ي ف فالخطان ب ا، ا س يطبقان على ي د، د ف والزاوية ب ا س تطبق على الزاوية ي د ف وتعدلها (أولية ٨)
وذلك ما كان علينا أن نبرهنه
القضية التاسعة.ع
علينا أن ننصّف زاوية بسيطة مستقيمة مفروضة أي أن نقسمها إلى قسمين متساويين
ليكن ب ا س الزاوية المفروض أن ننصفها عيّن أيَّة نقطة شئت في الخط ا ب كالنقطة د من ا س أطول خطَّين اقطع جزاءً ا ي حتى يعدل ا د أقصرهما (ق ٣ ك ١)
ارسم الخطَّ د ي وأبنِ عليهِ مثلثاً متساوي الأضلاع د ق ي (ق ١ ك ١)
وارسم الخط ا ق فهو ينصَّف الزاوية ب ا س
لأن الخط ا د يعدل الخط ا ي والخط ا ق مشترك بين المثلثين د ا ق، ي ا ق فالضلعان د ا، ا ق يعدلان الضلعين ي ا، ا ق كل واحد يعدل نظيرهُ.
والقاعدة د ق تعدل القاعدة ق ي فالزاوية د ا ق تعدل الزاوية ي ا ق (ق ٨ ك ١)
فقد تنصف الزاوية ب ا س بالخط ا ق المستقيم.
وذلك ما كان علينا أن نعملهُ تعليقة. على هذه الكيفية تنصف كلا النصفين ذ ا ق، ي ا ق وعلى هذا النسق يقسم زاوية مفروضة إلى أربعة أو ثمانية أجزاء أو إلى ستة عشر جزاءً متساوية وهلمَّ جرَّا
القضية العاشرة.ع
علينا أن ننصف خطَّاً مستقيماً محدوداً مفروضاً أي أن نقسمه إلى قسمين متساويين
ليكن ا ب الخط المستقيم المفروض علينا أن ننصفه
أرسم على الخط ا ب مثلثاً متساوي الأضلاع ا س ب (ق ١ ك ١)
ونصف الزاوية ا س ب بالخط المستقيم س د (ق ٩ ك ١)
فالخط ا ب قد انتصف في النقطة د
فلأن الخط ا س يعدل س ب والخط س د مشترك بين المثلثين ا س د ب س د فالضلعان ا س س د يعدلان الضلعين ب س س د والزاوية ا س د تعدل الزاوية ب س د فلذلك القاعدة ا د تعدل القاعدة ب د (ق ٤ ك ١)
فقد انتصف الخط ا ب في النقطة د
وذلك ما كان علينا أن نعملهُ
القضية الحادية عشرة.ع
علينا أن نرسم من نقطة مفروضة في خط مستقيم محدود مفروض خطاً مستقيماً يُحدِث مع الأول زاويتين قائمتين
ليكن ا ب الخط المستقيم المفروض و س النقطة المفروضة فيهِ.
فعلينا أن نرسم من النقطة س خطاً مستقيماً يحدث مع ا ب قائمتين
عَيِّنْ أيَّة نقطة شيئت في ا س كالنقطة د مثلاً ومن س ب اقطع جزاءس ي حتى يعدل س د (ق ٣ ك ١)
وعلى د ي ابنِ مثلثاً متساوي الاضلاع (ق ١ ك ١)
د ق ي ثم ارسم الخط ق س فهو يحدث مع ا ب قائمتين
فلأنَّ د س يعدل ي س والخط ق س هو مشترك بين المثلثين د س ق، ي س ق فالضلعان د س، س ق يعدلان الضلعين ي س، س ق كل واحد يعدل نظيره.
والقاعدة د ق تعدل القاعدة ي ق فالزاوية د س ق تعدل الزاوية ي س ق (ق ٨ ك ١) وهما متواليتان.
وإذا قام خط مستقيم على آخر مستقيم وجعل الزاويتين المتواليتين متساويتين فكل واحدة منهما قائمة (حد ٧)
فكل واحدة من د س ق، ي س ق قائمة.
فقد رُسِمَ من النقطة المفروضة س خطٌ ق س وهو يحدث مع ا ب قائمتين
وذلك ما كان علينا أن نعملهُ
القضية الثانية عشرة.ع
علينا أن نرسم خطاً عمودياً على خط مستقيم مفروض غير محدود وذلك من نقطة مفروضة خارج ذلك الخط
ليكن ا ب خطَّاً مستقيماً يمكن إخراجه إلى جهتيهِ إلى غير نهاية.
ولتكن س نقطةً خارجهُ فعلينا أن نرسم من س خطاً عمودياً على ا ب
عَيِّنْ أية نقطة شيئت على الجانب الآخر من ا ب مثل د ثم اجعل س مركزاً و س د بعداً وارسم الدائرة ي غ ق (ثالثة الممكنات) التي تقطع ا ب في النقطتين غ و ق.
نصّف ق غ في ح (ق ١٠ ك ١) ثم ارسم س ح فهو عمودي على ا ب.
ارسم س ق، س غ ولأن ق ح يعدل ح غ والخط س ح مشترك بين المثلثين ق ح س، غ ح س فالضلعان ق ح، ح س يعدلان الضلعين غ ح، ح س كل واحد يعدل نظيره.
والقاعدة س ق تعدل القاعدة س غ (حد ١١)
فالزاوية ق ح س تعدل الزاوية غ ح س (ق ٨ ك ١) وهما متواليتان.
فالخط س ح عمودي على ا ب (حد ٧)
وقد رُسِم من النقطة المفروضة س
وذلك ما كان علينا أن نعملهُ
القضية الثالثة عشرة.ن
الزاويتان الحادثتان من وقوع خط مستقيم على آخر مستقيم على جانب واحد منه هما قائمتان أو تعدلان قائمتين
ليقع الخط المستقيم ا ب على الخط المستقيم د س حتى تحدث الزاويتان ا ب د، ا ب س فهما قائمتان أو تعدلان قائمتين
فإذا كان ا ب د، ا ب س متساويتين فهما قائمتان (حدّ ٧)
وإلا فمن النقطة ب ارسم الخط ب ي عمودياً على د س (ق ۱۱ ك ۱)
فالزاويتان ي ب د، ي ب س قائمتان، والزاوية س ب ي تعدل س ب ا مع ا ب ي
أضف إلى كل واحدة منهما ي ب د فالزاويتان س ب ي، ي ب د تعدلان الثلاث زوايا س ب ا، ا ب ي، ي ب د (أولية ۲)
والزاوية د ب ا تعدل د ب ي مع ي ب ا أضف إلى كل واحدة منهما ا ب س فالزاويتان د ب ا، ا ب س تعدلان الثلاث د ب ي، ي ب ا، ا ب س
وقد تبرهن أن د ب ي، س ب ي تعدل هذه الثلاث زوايا أيضاً.
والأشياء المساوية لشيء واحد هي متساوية بعضها لبعض (أولية ۱)
أي الزاويتان س ب ي، د ب ي تعدلان الزاويتين د ب ا، ا ب س ولكن س ب ي، ي ب د هما قائمتان فالزاويتان د ب ا، ا ب س تعدلان قائمتين
فرعٌ. مجتمع جميع الزاويا الحادثة على جانب واحد من د س يعدل قائمتين لأنه يعدل مجتمع د ب ا، ا ب س
القضية الرابعة عشرة.ن
إذا وقع خطَّان مستقيمان على نقطة واحدة من خطٍّ آخر مستقيم عن جانبيهِ واحدثا زاويتين متواليتين تعدلان قائمتين فالخطَّان على استقامة واحدة كأنَّها خطٌّ واحدٌ
ليقع خطَّان س ب، د ب على النقطة ب من الخط ا ب من جانبيه وليحدثا زاويتين متواليتين تعادلان قائمتين ا ب س، ا ب د فالخطان س ب، ب د على استقامة واحدة كإنهما خط واحد
وإلا فارسم ب ي حتى يكون س ب، ب ي على استقامة واحدة فالخط المستقيم ا ب الواقع على خط اخر مستقيم س ي على جانب واحد منه يحدث زاويتين ا ب س، ا ب ي تعادلان قائمتين (ق ۱۳ ك ۱)
ولكن قد فُرِض أن ا ب س، ا ب د تعادلان قائمتين فالزاويتان ا ب س، ا ب ي تعدلان ا ب س، ا ب د أطرح الزاوية المشتركة ا ب س فالباقية ا ب ي تعدل الباقية ا ب د (أولية ۳)
أي الجزء يعدل الكل وذاك محال فلا يمكن أن يكون س ب، ب ي على استقامة واحدة.
وهكذا في كل خط غير ب د فالخطان س ب، ب د المحدثان مع �� ب زاويتين تعدلان قائمتين هما على استقامة واحدة
وذلك ما كان علينا أن نبرهنه
القضية الخامسة عشرة.ن
إذا تقاطع خطَّان مستقيمان فالزوايا المتقابلة متساوية
ليكن ا ب خطَّا مستقيماً فالزاوية س ي ا تعدل ا ي د
لأنّ الزاويتين س ي ا، ا ي د الحادثتين من وقوع على س د تعدلان قائمتين (ق ۱۳ ك ۱) و ا ي د، د ي ب الحادثتان من وقوع د ي على ا ب أيضاً تعدلان قائمتين (ق ۱۳ ك ۱)
فالزاويتان س ي ا، ا ي د تعدلان ا ي د، د ي ب اطرح المشتركة ا ي د فالباقية س ي ا تعدل الباقية د ي ب (أولية ۳)
وهكذا أيضاً يبرهن أن س ي ب تعدل ا ي د
فرع أوّلٌ. يتضح من هذه القضية ان مجتمع جميع الزوايا الحادثة من تقاطع خطَّين مستقيمين يعدل أربع زوايا قائمة
فرعُ ثانٍ. مجتمع الزوايا الحادثة من تقاطع خطوط مستقيمة في نقطة واحدة يعدل أربع زوايا قائمة
القضية السادسة عشرة.ن
إذا اخرِجَ ضلع من مثلث فالزاوية الخارجة الحادثة من ذلك هي أكبر من إحدى الداخلتين المتقابلتين
ليكن ق ب س مثلثاً وليخرج الضلع ب س إلى د فالزاوية الخارجة ق س د هي أكبر من إحدى الداخلتين المتقابتين س ب ق، ب ق س نصّف ق س في ي (ق ۲ ك ۱) ارسم ا س واخرج ق س إلى غ
فلأن ق ي يعدل ى س و ب ي يعدل ي ا فالخطَّان ق ي، ي ب يعدلان ا ي، ي س كل واحد يعدل نظيره.
والزاوية ق ي ب تعدل ا ي س (ق ۱٥ ك ۱)
فالقاعدة ق ب تعدل القاعدة ا س (ق ٤ ك ۱)
والمثلث ق ي ب يعدل المثلث ا ي س وبقية الزوايا من الواحد تعدل بقية الزاوية ي س ا والزاوية ي س د أو ق س د هي أكبر من ي س ا فهي إيضاً أكبر من ب ق ي أو ب ق س
وعلى هذا النسق إذا نُصِّف ب س يبرهن أن الزواية ب س غ أو ق س د (ق 15 ك 1) هي أكبر من ق ب س
القضية السابعة عشرة.ن
زاويتان من مثلث هما معاً أصغر من قائمتين
ليكن ا ب س مثلثاً فزاويتان منه معاً أصغر من قائمتين
أخرج ب س إلى د فالزاوية الخارجة ا س د هي أكبر من الداخلة ا ب س (ق ١٦ ك ١)
أضف إلى كل واحدة منهما ا س ب فالزاويتان ا س د، ا س ب معاً أكبر من ا ب س، ا س ب معاً ولكن ا س ب معاً تعدلان قائمتين (ق ١٣ ك ١)
وإذ ذاك فالزاويتان ا ب س، ا س ب معاً أصغر من قائمتين.
وعلى هذا الأسلوب يبرهن أن ب ا س، ا س ب معاً و س ا ب، ا ب س معاً أصغر من قائمتين.
القضية الثامنة عشرة.ن
الضلع الأطول من كل مثلث تقابلهُ الزاوية الكبرى
ليكن ا ب س مثلثاً وليكن الضلع ا س أطول من الضلع ا ب فتكون الزاوية ا ب س أكبر من الزاوية ب س ا
من ا س أقطع ا د حتى يعدل ا ب (ق ٣ ك ١)
وارسم ب د ففي المثلث د ب س الزاوية الخارجة ا د ب هي أكبر من الداخلة د س ب ولكن ا د ب تعدل (ق ٥ ك ١)
فالزاوية ا ب د أيضاً أكبر من د س ب وبالأحرى ا ب س أكبر من د س ب أي ا س ب
القضية التاسعة عشرة.ن
الزاوية الكبري من كل مثلث يقابلها الضلع الأطول ليكن ا ب س مثلثاً ولتكن الزاوية ا ب س أكبر من ا س ب فيكون الضلع ا س أطول من ا ب، وإلا فالضلع ا س يعدل ا ب، أو هو أقصر منه ولا يمكن أن يعدل ا ب لإنه عند ذلك كانت الزاويتان ا س ب، ا ب س متساويتين (ق ٥ ك ۱)
وقد فرض أن ا ب س أكبر من ا س ب ولو كان أقصر لكانت ا ب س أصغر من ا س ب (ق ۱۸ ك ۱)
فبالضرورة يكون ا س أطول من ا ب
ضلعان من مثلث هما معاً أطول من ضلعهِ الثالث
ليكن ا ب س مثلثاً فضلعان منه معاً أطول من ضلعه الثالث.
أي الضلعيان ب ا، ا س معاً أطول من ب س و ا ب، ب س معاً أطول من ا س و ب س، س ا معاً أطول من ا ب
أخرج ب ا إلى د واجعل ا د يعدل ا س (ق ۲ ك ۱)
وارسم د س فيما أكبر من ا س د فهي أيضاً أكبر من ا د س فيكون الضلع ب د أطول من ب س (ق ۱۹ ك ۱)
ولكن ب د يعدل ب ا مع ا س فالضلعان ب ا، ا س معاً هما أطول من ب س وهكذا في كل ضلعين من المثلث
تعليقة. يبرهن ذلك بدون أخراج ضلعٍ من المثلث لأن ب س هو البعد الأقرب بين النقطة ب والنقطة س فيكون ب س أقصر من ب ا، ا س أي ب ا، ا س معاً أطول من ب س
إذا رُسِمَ من طرفَي ضلع مثلث خطان مستقيمان إلى نقطة داخل المثلث
فهما أقصر من ضلعَي المثلث الآخرين ولكن يحيطان بزاوية أكبر من التي بين الآخرين
ليكن ا ب س مثلثاً. ولُيرسَم من طرفَي ب س خطان إلى النقطة د داخل المثلث مثل ب د، س د فهما أقصر من ب ا، ا س ولكن الزاوية ب د س هي أكبر من ب ا س. أخرج ب د إلى ي. فالضلعان ب ا أي معاً من المثلث ب ا ي هما أطول من ب ي (ق ۲۰ ك ۱)
أضف لهما ي س فالضلعان ب ا، ا س أطول من ب ي، ي س وفي المثلث س ي د الضلعان س ي، ي د هما أطول من س د.
أضف لهما د ب فالضلعان س ي، ي ب معاً أطول من س د، د ب.
وقد تبرهن أن ب ا، ا س هما معاً أطول من ب ي، ي س فالبلأحرى ب ا، ا س أطول من ب د، د س ثم الزاوية الخارجة ب د س من المثلث س د ي هي أكبر من الداخلة س ي د (ق ۱٦ ك ۱)
ولذات هذا السبب س �� د هي أكبر من ي ا ب أو س ا ب وقد تبرهن أن س د ب هي أكبر من س ي ب فبالأحرى هي أكبر من س ا ب
علينا أن نرسم مثلثاً اضلاعهُ تعدل ثلاثة خطوط مستقيمة مفروضة وكل اثنين منها معاً أطول من الثالث
ليكن ا و ب و س الخطوط المستقيمة المفروضة كل اثنين منها معاً أطول من الثالث. فعلينا أن نرسم مثلثاً أضلاعه تعدل هذه الخطوط الثلاثة
خذ خطًّا مستقيماً ينتهي في نقطة د وغير محدود من جهة ي واقطع منه د ق حتى يعدل ا (ق ۳ ك ۱)
و ق غ حتى يعدل ب و غ ح حتى يعدل س ثم أجعل ق مركزاً و ق د بعداً (ثالثة الممكنات)
وارسم دائرة د ك ل واجعل غ مركزاً و غ ح بعداً وارسم دائرةك ح ل (ثالثة الممكنات)
ومن ك أي نقطة تقاطع الدائرتين ارسم ك ق، ك غ فالمثلث ق ك غ هو المطلوب وأضلاعه تعدل الخطوط الثلاثة المفروضة ا و ب و س.
فقد جعلنا ق غ حتى يعدل ب ومن حيث أن النقطة ق هي مركز الدائرة د ك ل فالخط ق ك يعدل ق د (حد ۱۱) ولكن ق د يعدل فالخط ق ك يعدل ا أيضاً.
ومن حيث أن النقطة غ هي مركز الدائرة ك ح ل فالخط غ ح يعدل غ ك (حد ۱۱) ولكن غ ح يعدل س ولذلك غ ك يعدل س أيضاً فقد رُسِم مثلث أضلاعه تعدل ثلاثة خطوط مستقيمة مفروضة
تعليقة. لو كان أحد الأضلاع أطول من مجتمع الآخرين لما تقاطعت الدائرتان والقضية صحيحة كل ما كان مجتمع ضلعين أطول من الثالث
القضية الثالثة والعشرون.ن
علينا أن نرسم من نقطة مفروضة في خط مستقيم مفروض زاوية مستقيمة بسيطة حتى تعدل زاوية اخرى مسقيمة بسيطة مفروضة
ليكن ا س الخط المستقيم المفروض و ا النقطة المفروضة منه و د س ي الزاوية البسيطة المفروضة فعلينا أن نرسم من النقطة ا زاوية بسيطة تعدل د س ي. في س د عيّن أية نقطةٍ شئت مثل د. كذلك عين ي في س ي. أرسم د ي وارسم المثلث ا ق غ حتي يعدل المثلث س د ي (ق ۲۰ ك ۱) أي الضلع ا ق يعدل س د والضلع ا غ يعدل س ي والضلع ق غ يعدل د ي فيما أن الضلعين ق ا، ا غ يعدلان د س، س ي والقاعدة ق غ تعدل القاعدة د ي فالزاوية ق ا غ تعدل الزاوية د س ي (ق ٨ ك ۱) وقد رُسِمت من النقطة ا في الخط المفروض ا س
القضية الرابعة والعشرون.ن
في مثلثين إذا عدل ضلعان من الواحد ضلعَين من الاخر وكانت الزاوية الحادثة بين ضلعَي الاول أكبر من الحادثة بين ضلعَي الاخر فالذي لهُ الزاوية الكبري لهُ أيضاً القاعدة الطولي
ليكن ا ب س، د ي ف مثلثين ولنفرض أن الضلع ا بيعدل د ي والضلع ا س يعدل د ف ولكن الزاوية ب ا س أكبر من ي د ف فتكون القاعدة ب س أطول من القاعدة ي ف
ليكن د ف أطول من د ي ومن النقطة د ارسم الزاوية ي د غ حتى تعدل ب ا س (ق ٢٣ ك ١) واجعل د غ حتى يعدل ا س أو د ف ارسم ي غ، ف غ
فمن حيث أن ا ب يعدل القاعدة ي غ (ق ٤ ك ١) ومن حيث أن د ف يعدل د غ فالزاوية د ف غ تعدل د غ ف (ق ٥ ك ١)
ولكن الزاوية د غ ف هي أكبر من ي غ ف فتكون د ف غ أيضاً أكبر من ي غ ف فكم بالأحرى تكون ي غ ف أكبر من ي غ ف وفي المثلث ي غ ف فمن حيث أن الزاوية ي ف غ هي أكبر من ي غ ف فيكون الضلع ي غ أطول من ي ف (ق ١٩ ك ١) ولكن ي غ يعدل ب س فالقاعدة ب س أطول من القاعدة ي ف
إذا عدل ضلعا مثلثٍ ضلعَي مثلثٍ آخر ولكن كانت قاعدة احدهما أطول من قاعدة الآخر فالزاوية الكبرى هي لذي القاعدة الطولى ليكن ا ب س، د ي ف مثلثين ولنفرض أن ضلعين من الواحد ا ب، ا س عدلا ضلعين من الاخر د ي، د ف ولكن القاعدة ب س أطول من القاعدة ي ف فتكون الزاوية ب ا س أكبر من الزاوية ي د ف وإلاَّ فإما أن تعدلها أو تكون أصغر منها فالزاوية ب ا س لا تعدل ي د ف لأنه عند ذلك كانت القاعدة ب س تعدل القاعدة ي ف (ق ٤ ك ١)
وقد فرض ب س الأكبر ولا يمكن أن تكون أصغر منها لانه عند ذلك كانت القاعدة ب س أصغر من ي ف (ق ٢٤ ك ١) وقد فرض ب س أكبر وقد تبرهن أنها لا تعدلها فبالضرورة تكون الزاوية ب ا س أكبر من الزاوية ي د ف
القضية السادسة والعشرون.ن
إذا عدلت زاويتان من مثلثٍ زاويتين من مثلثٍ آخر أي كل واحدة عدلت نظيَرها. وضلعٌ من الواحد عدل ضلعاً من الآخران كانا المتواليين للزوايا المتساوية أو المتقابلَين لها فالضلعان الاخران من الواحد يعدلان الاخرين من الآخر والزاوية الثالثة من الواحد تعدل الثالثة من الآخر ب ا س تعدل الثالثة من الآخر ي د ف
وان لم يكن ا ب و د ي متساويين فبالضرورة يكون أحدهما أطول من الاخر فلنفرض ا ب الأطول ولنفصل منه ب غ حتى يعدل د ي (ق ٣ ك ١)
ولنرسم غ س فمن حيث أن غ ب يعدل د ي و ب س يعدل ي ف فالضلعان غ ب، ب س يعدلان الضلعين د ي، ي ف كل واحد يعدل نظيره والزاوية غ ب س تعدل د ي ف فالقاعدة غ س تعدل القاعدة د ف (ق ٤ ك ١)
والمثلث غ ب س يعدل المثلث د ي ف وبقية الزوايا من الواحد تعدل بقية الزوايا من الآخر كل واحدة تعدل نظيرها أي التي تقابلها الاضلاع المتساوية.
فالزاوية غ س ب تعدل ا س ب أي الأصغر يعدل الأكبر وذاك محال فلا يمكن أن يكون ا ب و د ي غير متساويين أي هما متساويان و ب س يعدل ي ف فالضلعان ا ب، ب س يعدلان الضلعين د ي، ي ف والزاوية ا ب س تعدل د ي ف فالقاعدة ا س تعدل القاعدة د ف (ق ٤ ك ١) والزاوية ب ا س تعدل الزاوية ي د ف
ثم لنفرض مساواة الضلعين اللذين يقابلان الزاويا المتساوية في كلا المثلثين يعني أن ا ب يعدل د ي فعلى هذا المفروض أيضاً لنا مساواة بقية الاضلاع يعني ا س يعدل د ف و ب س يعدل ي ف والزاوية الثالثة من الواحد ب ا س تعدل الثالثة من الآخر ي د ف فإن لم يكن ب س و ي ف متساويين فليكن ب س أطولهما.
أفصل منه ب ح حتى يعدل ي ف (ق ٣ ك ١) وارسم ا ح فمن حيث أن ب ح يعدل ي ف و ا ب يعدل د ي فالضلعان ا ب، ب ح يعدلان الضلعين د ي، ي ف والزاوية ا ب ح تعدل د ي ف فالقاعدة ا ح تعدل القاعدة د ف (ق ٤ ك ١) والمثلث ا ب ح يعدل المثلث د ي ف وبقية الزوايا أيضاً متساوية أي التي تقابلها الاضلاع المتساوية فالزاوية ب ح ا تعدل ي ف د ولكن ي ف د تعدل ب س ا فالزاوية ب س ا تعدل ب ح ا أي الزاوية الخارجة ا ح ب تعدل الداخلة المتقابلة ا س ب وذلك لا يمكن (ق ١٦ ك ١) فلا يمكن أن يكون ب س و ي ف غير متساويين أي هما متساويان و ا ب يعدل د ي فالضلعان ا ب، ب س يعدلان د ي، ي ف والزاوية ا ب س تعدل د ي ف فالقاعدة د ف والزاوية الثالثة ب ا س تعدل الثالثة ي د ف
القضية السابعة والعشرون.ن
إذا وقع خطٌّ مستقيم على خطين آخرين مستقيمين وجعل الزاويتين المتبادلتين متساويتين فالخطان متوازيان
ليقع الخط المستقيم ي ق على الخطين المستقيمين ا ب، س د وليجعل معهما الزاويتين المتبادلتين ا ي ق، ي ق د متساويتين فالخطان ا ب، س د متوازيان
وإلاَّ فليتقيان إذا أخرجا. فلنفرض التقائهما في النقطة غ ي ق مثلثاً وزاوية الخارجة ا ي ق تكون أكبر من الداخلة المتقابلة ي ق غ (ق ١٦ ك ١)
وقد فرض مساواتها فلا تكون أحداهما أكبر من الآخرى فلا يلتقي ا ب و س د إذا أخرجا إلى جهة ب و د وهكذا يبرهن أنهما لا يلتقيان إذا أخرجا إلى جهة ا و س فهما إذاً متوازيان (حد ٣٠)
القضية الثامنة والعشرون.ن
إذا وقع خطٌّ مستقيم على خطين مستقيمين واحدث زاويةً خارجةً تعدل الداخلة المتقابلة على جانب واحد منهُ أو داخلتين على جانب واحد منه تعدلان معاً قائمتين فالخطان متوازيان ليقع الخط المستقيم ي ف على الخطين المسقيمين ا ب، س د وليجعل معهما الزاوية الخارجة ي غ ب أن تعدل الداخلة المتقابلة على ذلك الجانب غ ح د أو ليجعل الداخلتين على جانب واحد ب غ ح، غ ح د إن تعدلا قائمتين فالخطان ا ب، س د متوازيان.
فمن حيث أن ي غ ب تعدل غ ح د وتعدل أيضاً ا غ ح (ق ١٥ ك ١)
فالزاوية ا غ ح تعدل غ ح د وهما متبادلتان ولذلك (ق ٢٧ ك ١)
ا ب يوازي س د وأيضاً من حيث أن ب غ ح، غ ح د تعدلان قائمتين حسب المفروض و ا غ ح، ب غ ح تعدلان قائمتين (ق ١٣ ك ١)
فالزاويتان ب غ ح، ا غ ح تعدلان ب غ ح، غ ح د اطرح المشتركة ب غ ح فالباقية ا غ ح تعدل الباقية غ ح د وهما متبادلتان ولذاك (ق ٢٧ ك ١) ا ب يوازي س د وأيضاً من حيث أن ب غ ح، غ ح د تعدلان قائمتين حسب المفروض و ا غ ح، ب غ ح تعدلان قائمتين (ق ١٣ ك ١)
فالزاويتان ب غ ح، ا غ ح تعدلان ب غ ح، غ ح د أطرح المشتركة ب غ ح فالباقية ا غ ح تعدل الباقية غ ح د وهما متبادلتان. ولذلك ا ب و س د متوازيان
فرعٌ. إذا ان كان خطان مستقيمان عموديَّين على خط مستقيم ثالث فهما متوازيان
القضية التاسعة والعشرون.ن
إذا وقع خطّ مستقيم على خطَّين مستقيمين متوازيين فالزاويتان المتبادلتان الحادثتان متساويتان والزاوية الخارجة تعدل الداخلة المتقابلة على جانب واحد والداخلتان على جانب واحد تعدلان قائمتين
ليقع الخط المستقيم ي ق على المتوازيين ا ب، س د فالزاويتان المتبادلتان ا غ ح، غ ح د متساويتان والخارجة ي غ ب تعدل الداخلة المتقابلة على ذلك الجانب غ ح د والداخلتان على جانب واحد ب غ ح، غ ح د تعدلان قائمتين
فإن لم تكن ا غ ح، غ ح د متساويتين فليرسم الخط ك غ حتى أن ك غ ح تعدل غ ح د واخرج ك غ إلى ل فالخط ك ل يوازي س د (ق ٢٧ ك ١) و ا ب أيضاً يوازي س د فقد رُسِم خطان مستقيمان مارَّان بنقطة واحدة غ يوازيان س د من غير أن يتطابقا وذلك محال (أولية ۱۱) فلا تكون الزاويتان ا غ ح، غ ح د غير متساويتين أي هما متساويتان.
والزاوية ي غ ب تعدل ا غ ح (ق ۱٥ ك ۱) ولذلك ي غ ب أيضاً تعدل غ ح د (أولية أولى)
أضف إليها ب غ ح فالزاويتان ي غ ب، ب غ ح تعدلان ب غ ح، غ ح د ولكن ي غ ب، ب غ ح تعدلان قائمتين (ق ۱۳ ك ۱) ولذلك ب غ ح، غ ح د تعدلان قائمتين أيضاً
فرع أول. إذا جعل الخطان ك ل، س د مع ي ق الزاويتين ك غ ح، غ ح س معاً أصغر من قائمتين فالخطان ك غ، س ح يلتقيان على ذلك الجانب ي ق الذي فيه كانت الزاويتان أصغر من قائمتين
وإلا فهما متوازيان. أو يلتقيان على الجانب الآخر من الخط ي ق ولكنهما غير متوازيين. وإلا لكانت ك غ ح، غ ح س معاً تعدلان قائمتين ولا يلتقيان على الجانب الآخر من الخط ي ق وإلا لكانت ل غ ح، غ ح د زاويتين من زوايا مثلث وأصغر من قائمتين وذلك لا يمكن لأن الأربع زوايا ك غ ح، ح غ ل، س ح غ، غ ح د تعدل أربع زوايا قائمة (ق ۱۳ ك ۱)
واثنتان منها أي ك غ ح، غ ح س هما بالمفروض أصغر من قائمتين فبالضرورة الآخريان ل غ ح، غ ح د أكبر من قائمتين فمن حيث أن ك ل، س د غير متوازيين ولا يلتقيان من جهة ل و د فالضرورة يلتقيان إذا أخرجا إلى جهة ك و س
فرعٌ ثان. إذا كان ب غ ح قائمة تكون غ ح د أيضاً قائمة فالخط العمودي على أحد خطيَّن متوازيين هو عموديٌّ على الآخر أيضاً
فرعٌ ثالث. من حيث أن ا غ ي = ب غ ح و د ح ق = س ح غ تكون الأربع الزوايا الحادَّة ا غ ي، ب غ ح، س ح غ، د ح ق متساوية. وهكذا الأربع الزوايا المنفرجة ي غ ب، ا غ ح، غ ح د، س ح ق هي أيضاً متساوية. وإذا اضيفت إحدى الحادَّات إلى إحدى المنفرجات فالمجموع يعدل قائمتين.
تعليقة. الزاويا المذكورة لها أسماء مختلفة باعتبار نسبة بعضها إلى بعض فالزاويتان ب غ ح، غ ح د هما الداخلتان على جانب ��احد وكذلك ا غ ح، غ ح س. والزاويتان ا غ ح، غ ح د هما الداخلتان المتبادلتان أو المتبادلتان فقط. وكذلك ب غ ح، غ ح س. والزاويتان ي غ ب، غ ح د هما الخارجة والداخلة وكذلك ي غ ا، غ ح س والزاويتان ي غ ب، س ح ق هما الخارجتان المتبادلتان وكذلك ا غ ي، د ح ق
القضية الثلاثون.ن
الخطوط المستقيمة المتوازية لخطٍ واحدٍ مستقيم هي متوازية بعضها لبعض
ليقع على ا ب، ي ف، س د الخط المستقيم غ ح فمن حيث أن ا ب، ي ف متوازيان فالزاوية ا غ ح تعدل الزاوية غ ح ف (ق ٢٩ ك ١) ومن حيث أن ي ف، س د متوازيان فالزاوية غ ح ف تعدل غ ك د (ق ٢٩ ك ١)
وقد تبرهن أن ا غ ح تعدل غ ح ف فلذلك ا غ ح تعدل غ ك د أيضاً وهما متبادلتان فالخط ا ب يوازي الخط س د (ق ٢٧ ك ١)
القضية الحادية والثلاثون.ن
علينا أن نرسم خطاً مستقيماً يمرّ في نقطة مفروضة ويوازي خطاً مستقيماً مفروضاً
لتكن ا النقطة المفروضة و ب س الخط المستقيم المفروض. علينا أن نرسم خطاً مستقيماً يوازي ب س ويمر بالنقطة ا
عيّن أية نقطة شئت في ب س كالنقطة مثلاً. أرسم ا د وفي النقطة ا من الخط ا د أرسم الزاوية د ا ي واجعلها أن تعدل الزاوية ا د س (ق ٢٣ ك ١) وأخرج ي ا إلى ف
فمن حيث أن الخط المستقيم ا د يلاقي الخطين المستقيمين ي ف، ب س ويجعل معهما الزاويتين المتبادلتين ي ي ا د، ا د س متساويتين فالخط ي ف يوازي ب س (ق ٢٧ ك ١) وقد رُسم حتي يمرّ في النقطة ا المفروضة القضية الثانية والثلاثون.ن
إذا اخرج ضلعٌ من أضلاع مثلثٍ فالزاوية الخارجة تعدل الداخلتين المتقابلتين. والزوايا الثلاث الداخلة من كل مثلث تعدل قائمتين
ليكن ا ب س مثلثاً وليخرج منه الضلع ب س إلى د فالزاوية الخارجة ا س د تعدل الداخلتين المتقابلتين س ا ب، ا ب س والزاويا الثلاث الداخلة ا ب س، ب س ا، س ا ب معاً تعدل قائمتين
من النقطة س ارسم الخط المستقيم س ي حتى يوازي ا ب (ق ٣١ ك ١) فمن حيث أن الخط ا س يلاقي الخطين المتوازيين ا ب، س ي فالزاويتان المتبادلتان ا س ي، ب ا س متساويتان (ق ٢٩ ك ١) ومن حيث أن ب د يلاقي المتوازيين ا ب، س ي فالزاوية الخارجة ي س د تعدل الداخلة المتقابلة ا ب س وقد تبرهن أن ا س ي تعدل ب ا س فكل الخارجة ا س د تعدل الداخلتين المتقابلتين ب ا س، ا ب س.
اضف إلى هذه الزوايا الزاوية ا س ب فالزاويتان ا س د، ا س ب تعدلان الثلاث زوايا ا ب س، ب ا س، ا س ب ولكن ا س د، ا س ب معاً تعدلان قائمتين (ق ١٣ ك ١) فالزوايا الثلاث ا ب س، ب ا س، ا س ب أيضاً تعدل قائمتين.
فرعٌ أول. جميع الزوايا الداخلة في كل شكل ذي أضلاع مستقيمة تعدل من الزوايا القائمة ما يماثل مضاعف عدد أضلاع الشكل إلا أربع زوايا قائمة
لأن كل شكل ذي أضلاع مستقيمة مثل ا ب س د ي ينقسم إلى مثلثات تماثل أضلاعه برسم خط مستقيم من كل زاوية إلى نقطة داخلهُ مثل ق فحسب هذه القضية زوايا كل مثلث تعدل قائمتين فجميع زوايا جميع المثلثات يعدل قائمتين في عدد أضلاع الشكل ولكن الزوايا عند ق تعدل زوايا قائمة (ق ١٥ ك ١ فرع ٢) فزوايا الشكل تعدل قائمتين في عدد أضلاع الشكل إلا أربع زوايا قائمة
فرعٌ ثان. مجتمع الزوايا الخارجة من كل شكل ذي أضلاع مستقيمة يعدل أربع زوايا قائمة. لأن كل زاوية داخلة ا ب س مع الخارجة المتوالية ا ب د تعدل قائمتين (ق ١٣ ك ١) فجميع الداخلة مع جميع الخارجة تعدل قائمتين في عدد أضلاع الشكل والداخلة تعدل قائمتين في عدد أضلاع الشكل إلا أربع قائمات حسب الفرع الأول فالخارجة تعدل أربع قائمات
فرعٌ رابع. إذا عدلت زاويتان من مثلثٍ زاويتين من مثلث آخر فالثالثة من الواحد تعدل الثالثة من الآخر والمثلثان متساويا الزوايا
فرعٌ خامس. لا يكون في مثلث أكثر من زاوية واحدة قائمة. لإنه لو كانت لهُ قائمتان لكانت الثالثة لا شيء. وبالأحرى لا يكون لمثلث أكثر من زاوية واحدة منفرجة
فرع سادس. في كل مثلث قائم الزاوية مجتمع الحادتين يعدل قائمة
فرع سابع. من حيث أن كل مثلث متساوي الأضلاع هو متساوي الزوايا أيضاً (فرع ق ٥ ك ١) فكل زاوية من زواياه تعدل ثلث قائمتين أو ثُلُثَي قائمة
فرع ثامن. مجتمع زوايا ذي أربعة أضلاع يعدل قائمتين في ٤ - ٢ أي أربع قائمات فإذا كانت زواياه متساوية تكون كل واحدة قائمة وذلك يؤيد الحدّ الخامس والعشرين والسادس والعشرين
فرع تاسع. مجتمع زوايا ذي خمسة أضلاع يعدل قائمتين في ٥ - ٢ أي ست قائمات فإذا كانت زواياه متساوية تكون كل واحدة خمس ست قائمات أي ٥٦ قائمة
فرع عاشر. مجتمع زوايا ذي ستة أضلاع تعدل ٢ × (٦ - ٢) أي ثمان قائمات فإذا كانت زواياهُ متساوية تكون كل واحدة سدس ثمان قائمات أي ٤٣ قائمة تعليقة. متى استعمل الفرع الأول في أشكال كثيرة الأضلاع لها زوايا متداخلة مثل ا ب س فيجب أن تحسب كل متداخلة أكبر من قائمتين وإذا رسم ب د، ب ي، ب ف ينقسم الشكل إلى أربع مثلثات لها ثماني قائمات أي قائمتان في عدد الأضلاع إلا اثنين
القضية الثالثة والثلاثون.ن
الخطان المستقيمان الموصلان بين أطراف خطَّين مستقيمين متوازيين متساويين هما متوازيان ومتساويان
ليكن ا ب و س د خطَّين مستقيمين متساويين متوازيين وليوصل بين أطرافهما بالخطين المستقيمين ا س، ب د فهذان الخطان أيضاً متوازيان متساويان
ارسم ب س فمن حيث أن ب س يلاقي الخطَّين المتوازيين ا ب، س د فالزاويتان المتبادلتان ا ب س، ب س د هما متساويتان (ق ٢٩ ك ١)
ومن حيث أن ا ب يعدل س د والخط ب س مشترك بين المثلثين ا ب س، ب س د فالضلعان ا ب، ب س يعدلان الضلعان ب س، س د والزاوية ا ب س تعدل ب س د فالقاعدة ا س تعدل القاعدة ب د (ق ٤ ك ١) وبقية الزوايا من الواحد تعدل بقية الزوايا من الاخر أي ا س ب تعدل س ب د.
ومن حيث أن الخط ب س يلاقي الخطين ا س، ب د ويجعل الزاويتين المتبادلتين ا س ب، س ب د متساويتين فالخطَّان ا س، ب د متوازيان (ق ٢٧ ك ١) وقد تبرهن أنهما متساويان
فرع أول. في كل شكل ذي أربعة أضلاع إذا كان ضلعان متقابلان متوازيين ومتساويين يكون الضلعان الاخران كذلك ويكون الشكل ذا أضلاع متوازية
فرع ثان. كل ذي أربعة أضلاع ضلعاهُ المتقابلان متساويان هو ذو أضلاع متوازية فرع ثالث. في كل ذي أربعة أضلاع إذا كانت الزوايا المتقابلة متساوية تكون الأضلاع المتقابلة متساوية ومتوازية
القضية الرابعة والثلاثون.ن
في شكل ذي أضلاع متوازيةٍ الأضلاعُ المتقابلة والزوايا المتقابلة هي متساوية. والقطر ينصفهُ أي يقسمهُ إلى جزئين متساويين
ليكن ا ب، د س متوازي الأضلاع و ب س قطرهُ فالأضلاع المتقابلة والزوايا المتقابلة متساوية والقطر ب س ينصفهُ
فمن حيث أن الخط ب س يلاقي الخطَّين المتوازيين ا ب، س د فالزاويتان المتبادلتان ا ب س، ب س د متساويتان (ق ٢٩ ك ١)
وأيضاً لأن ب س يلاقي المتوازيين ا س، ب د فالمتبادلتان ا س ب، س ب د متساويتان (ق ٢٩ ك ١)
ففي المثلثين ا ب س، ب س د زاويتان من الواحد تعدلان زاويتين من الاخر والضلع ب س مشترك بين المثلثين فالضلعان الآخران من الواحد يعدلان الضلعين الآخرين من الآخر والزاوية الثالثة من الواحد تعدل الثالثة من الآخر (ق ٢٦ ك ١)
أي ا ب يعدل س د و ا س يعدل ب د والزاوية ب ا س تعدل س د ب ولأن الزاوية ا ب س تعدل ب س د و ا س ب تعدل س ب د فكل الزاوية ا ب د تعدل كل الزاوية ا س د وقد تبرهن أن ب ا س تعدل ب د س فكل الزاوية ا ب د تعدل كل الزواية ا س د
وقد تبرهن أن ب ا س تعدل ب د س فالزاويا المتقابلة والأضلاع المتقابلة من ذي أضلاع متوازية هي متساوية وأيضاً القطر ينصفهُ فلأن ا ب يعدل س د و ب س مشترك بين المثلثين والزاوية ا ب س تعدل ب س د فالمثلثان متساويان (ق ٤ ك ١) وقد انتصف الشكل بالقطر
فرع أول. خطان متوازيان خطَّين متوازيين متساويان
فرع ثانٍ. خطان متوازيان هما على بعد واحد بعضهما من بعض أبداً
فرع ثالث. مجتمع زاويتين متواليتين من ذي أضلاع متوازية يعدل قائمتين
القضية الخامسة والثلاثون.ن
أشكال ذات أضلاع متوازية على قاعدة واحدة وبين خطين متوازيين هي متساوية
ليكن ا ب س د و ي ب س ف شكلين متوازيي الأضلاع على قاعدة واحدة ب س وبين خطين متوازيين ا ف، ب س فالشكل ا ب س د يعدل الشكل ي ب س ف.
إذا انتهى الضلعان ا د، د ف من الشكلين ا ب س د، د ب س ف المتقابلان للقاعدة ب س في نقطة واحدة د فالأمر واضح أن كل واحد من الشكلين إنما هو مضاعف المثلث ب د س (ق ٣٤ ك ١)
وإذ ذاك فهما متساويان وأن لم ينته في نقطة واحدة الضلعان ا د، ي ف من الشكلين ا ب س د، ي ب س ف المقابلان للقاعدة ب س
فثَمَّ من حيث أن ا ب س د متوازي الأضلاع فالضلع ا د يعدل ب س (ق ٣٤ ك ١) ولهذا السبب أيضاً ي ف يعدل ب س ولذلك ا د يعدل ي ف (أولية أولي)
و د ي مشترك فالكل أو البقية أي ا ي يعدل الكل أو البقية د ف (أولية ثانية وثالثة)
و ا ب يعدل د س فالضلعان ي ا، ا ب يعدلان الضلعين ف د، د س كل واحد يعدل نظيرَهُ والزاوية الخارجة ف د س تعدل الداخلة المتقابلة ي ا ب (ق ٢٩ ك ١)
فالقاعدة ي ب تعدل القاعدة ف س والمثلث ي ا ب يعدل المثلث ف د س (ق ٤ ك ١)
أطرح المثلث ف د س من الشكل ا ب س ف واطرح منهُ أيضاً ي ا ب فتكون البقايا متساوية (أولية ٣) أي الشكل ا ب س د يعدل الشكل ي ب س ف القضية السادسة والثلاثون.ن
أشكال ذات أضلاع متوازية على قاعدة متساوية وبين خطين متوازيين هي متساوية
ليكن ا ب س د و ي ف غ ح شكلين متوازيي الأضلاع على قاعدتين متساويتين ب س و ف غ وبين خطين متوازيين ا ح و ب غ فهما متساويان.
ارسم ب ي و س ح فمن حيث أن ب س يعدل ف غ و ف غ يعدل ي ح (ق ٣٤ ك ١)
فلذلك ي ح يعدل ب س أيضاً وهما متوازيان وقد أوصل بينهما إلى جهة واحدة بالخطين ب ي، س ح والخطوط الموصلة بين خطين متوازيين متساويين إلى جهة واحدة هي متوازية ومتساوية (ق ٣٣ ك ١) فالخطان ب ي، س ح متساويان متوازيان والشكل ي ب س ح متوازي الأضلاع وهو يعدل الشكل ا ب س د (ق ٣٥ ك ١)
لإنهما على قاعدة واحدة ب س وبين خطين متوازيين ب س، ا ح ولهذا السبب أيضاً الشكل ي ف غ ح يعدل ي ب س ح فالشكلان ا ب س د، ي ف غ ح متساويان
القضية السابعة والثلاثون.ن
مثلثات على قاعدة واحدة وبين خطين متوازيين هي متساوية
ليكن ا ب س، د ب س مثلثين على قاعدة واحدة ب س وبين خطًّين متوازيين ا د و ب س فهما متساويان
أخرج ا د إلى الجهتين إلى ف و ي (ق ٣١ ك ١) ومن س ارسم س ف حتى يوازي ب د فكل واحد من الشكلين ا ي ب س، د ب س ف متوازي الأضلاع وهما متساويان (ق ٣٥ ك ١) لإنهما على قاعدة واحدة ب س وبين خطين متوازيين ي ف و ب س والمثلث ا ب س هو نصف الشكل ا ي ب س لأن القطر ا ب ينصفهُ (ق ٣٤ ك ١) والمثلث د ب س هو نصف الشكل د ب س ف لأن القطر د س ينصفهُ وانصاف أشياء متساوية بعضها لبعض (أولية ٧) فالمثلث ا ب س يعدل د ب س.
القضية الثامنة والثلاثون.ن
مثلثات على قواعد متساوية وبين خطًّين متساويين هي متساوية
ليكن ا ب س و د ي ف مثلثين على قاعدتين متساويتين ب س، ي ف وبين خطين متوازيين ا د و ب ف فهما متساويان
أخرج ا د إلى الجهتين إلى ح و غ وارسم ب غ حتى يوازي ا س (ق ٣١ ك ١)
ومن ف ارسم ف ح حتى يوازي د ي فكل واحد من الشكلين ا غ ب س، د ي ف ح متوازي الاضلاع وهما متساويان (ق ٣٦ ك ١)
لأنهما على قاعدتين متساويتين ب س، ي ف وبين خطين متوازيين غ ح، ب ف والمثلث ا ب س هو نصف الشكل ا غ ب س (ق ٣٤ ك ١)
لأن القطر ا ب ينصفه و د ي ف هو نصف الشكل د ي ف ح (ق ٣١ ك ١) لأن القطر د ف ينصفه وانصاف أشياء متساوية هي متساوية (أولية ٧) فالمثلث ا ب س يعدل المثلث د ي ف
القضية التاسعة والثلاثون.ن
مثلثات متساوية على قاعدة واحدة وعلى جانب واحد منها هي بين خطًّين متوازيين
ليكن ا ب س و د ب س مثلثين متساويين على قاعدة واحدة ب س وعلى جانب واحد منها فهما بين خطين متوازيين
ارسم ا د فالخط ا د يوازي ب س وإلا فمن النقطة ا ارسم ا ي حتى يوازي ب س (ق ٣١ ك ١)
وارسم ي س فالمثلث ا ب س يعدل المثلث ي ب س (ق ٣٧ ك ١)
لأنهما على قاعدة واحدة ب س وبين خطين متوازيين ب س، ا ي والمثلث ا ب س يعدل د ب س فالمثلث ي ب س يعدل د ب س
أي الأصغر يعدل الأكبر وذاك محال فلا يمكن أن يكون ب س و ا ي متوازيين وهكذا يبرهن في كل خط إلا الخط ا د فهو يوازي ب س
القضية الأربعون.ن
مثلثات متساوية على قواعد متساوية وعلى جانب واحد منها هي بين خطًّين متوازيين إذا كانت القواعد على استقامة واحدة
ليكن ا ب س، د ي ف مثلثين متساويين على قاعدتين متساويتين وعلى استقامة واحدة ب س ي ف وعلى جانب واحد منها فهما بين خطَّين متوازيين
ارسم ا د فهو يوازي ب ف وإلا فارسم ا غ حتى يوازي ب ف (ق ٣١ ك ١)
وارسم غ ف فالمثلث ا ب س يعدل المثلث غ ي ف (ق ٣٨ ك ١)
لأنهما على قاعدتين متساويتين ب س ي ف وبين خطَّين متوازيين ب ف، ا غ
ولكن المثلث ا ب س يعدل المثلث د ي ف فلذلك المثلث د ي ف يعدل المثلث غ ي ف أي الأكبر يعدل الأصغر وذاك محال فالخط ا غ لا يوازي ب ف
وهكذا يبرهن في كل خط ما عدا ا د فهو يوازي ب ف
القضية الحادية والأربعون.ن
إذا كان شكل ذو اضلاع متوازية ومثلث على قاعدة واحدة وبين خطين متوازيين فالشكل مضاعف المثلث
ليكن الشكل ذو الأضلاع المتوازية ا ب س د والمثلث ي ب س على قاعدة واحدة ب س وبين خطين متوازيين ا ي، ب س فالشكل ا ب س د مضاعف ي ب س
أرسم ا س فالمثلث ا ب س يعدل المثلث ي ب س (ق ٣٧ ك ١) لأنهما على قاعدة واحدة ب س وبين خطين متوازيين ا ي، ب س ولكن الشكل ا ب س د هو مضاعف المثلث ا ب س (ق ٣٤ ك ١) لأن القطر ا س ينصفهُ فالشكل ا ب س د مضاعف المثلث ي ب س أيضاً
القضية الثانية والأربعون.ع
علينا أن نرسم شكلاً ذا اضلاع متوازية حتى يعدل مثلثاً مفروضاً وزاوية من زواياه تعدل زاوية مستقيمة بسيطة مفروضة
ليكن ا ب س المثلث المفروض و د الزاوية البسيطة المفروضة علينا أن نرسم شكلاً ذا أضلاع متوازية حتى يعدل المثلث ا ب س وزاوية من زواياه تعدل د
نَصِف ب س في ي (ق ١٠ ك ١) أرسم ا ي ومن النقطة ي في الخط المستقيم ي س أجعل الزاوية س ي ف حتى تعدل د (ق ٢٣ ك ١)
ومن ا ارسم ا غ حتى يوازي ب س (ق ٣١ ك ١)
ومن س ارسم س غ حتى يوازي ي ف فالشكل س ي ف غ متوازي الأضلاع فمن حيث أن ب ي يعدل ي س فالمثلث ا ب ي يعدل المثلث ا ي س (ق ٣٨ ك ١)
لأنهما على قاعدتين متساويتين ب ي، ي س وبين خطين متوازي ا غ، ب س ولذلك المثلث ا ي س (ق ٤١ ك ١) لأنهما على قاعدة واحدة وبين خطَّين متوازيين فالشكل ف ي س غ يعدل المثلث ا ب س ولهُ الزاوية س ي ف التي تعدل الزاوية المفروضة د
فرعٌ. إذا كانت الزاوية د قائمة يكون الشكل ف ي س غ قائم الزاويا ويعدل المثلث ا ب س فبذات هذا العمل يصنع مثلث حتى يعدل شكلاً مفروضاً زواياهُ قائمة القضية الثالثة والأربعون.ن
الأجزاء المتمَّة لاشكل متوازية الأضلاع واقعةٍ على جانبي قطر شكل متوازي الأضلاع هي متساوية
ليكن ا ب س د شكلاً متوازي الأضلاع و ا س قطرهُ و ي ح و غ ف شكلين متوازيي الأضلاع على جانبي القطر ا س وليكن ب ك و ك د الشكلين الآخرين المتمين لكل الشكل ا ب س د فالمتمّ ب ك يعدل المتمم ك د
فمن حيث أن ا ب س د متوازي الأضلاع و ا س قطرهُ فالمثلث ا ب س يعدل المثلث ا د س (ق ٣٤ ك ١)
ومن حيث أن ا ي ك ح متوازي الأضلاع فالمثلث ا ي ك يعدل المثلث ا ح ك ولهذا السبب أيضاً المثلث ك غ س يعدل المثلث ك ف س فالمثلث ا ي ك مع ك غ س يعدل المثلث ا ح ك مع ك ف س والكل ا ب س يعدل الكل ا د س فالبقية ب ك تعدل البقية ك د (أولية ٣)
القضية الرابعة والأربعون.ن
علينا أن نرسم على خط مستقيم مفروض شكلاً متوازي الأضلاع حتى يعدل مثلثاً مفروضاً وزاوية من زواياه تعدل زاوية بسيطة مفروضة
ليكن ا ب الخط المستقيم المفروض و س المثلث المفروض و د الزاوية المفروضة.
علينا أن نرسم على الخط ا ب شكلاً متوازي الأضلاع حتى شكلاً متوازي الأضلاع حتى يعدل س وزاوية من زواياه تعدل د.
أرسم الشكل المتوازي الأضلاع ب ي ف غ حتى يعدل المثلث س (ق ٤٢ ك ١) واجعل الزاوية ي ب غ منهُ تعدل الزاوية د واجعل ضلعهُ ي ب والخط ا ب على استقامة واحدة واخرج ف غ إلى ح ومن ا ارسم ا ح حتى يوازي ب غ أو ي ف (ق ٣١ ك ١) وارسم ح ب.
فمن حيث ان الخط المستقيم ح ف يلاقي المتوازيين ح ا، ف ي فالزاويتان ا ح ف، ح ف ي معاً تعدلان قائمتين (ق ٢٩ ك ١)
فالزاويتان ب ح ف، ح ف ي معاً أقل من قائمتين ولا بد من إ��تقاء ح ب و ف ي إذا أخرجا (ق ٢٩ ك ١ فرع ١)
أخرجهما حتى يلتقيا في ك ومن ك ارسم ك ل حتى يوازي ي ا أو ف ح وأخرج ح ا إلى ل واخرج غ ب إلى م فالشكل ح ل ك ف متوازي الأضلاع وقطره ح ك والشكلان ا غ و م ي هما متوازيا الأضلاع على جانبي القطر ح ك.
و ل ب و ب ف هما المتَّمان فالمتم ل ب يعدل المتم ب ف (ق ٤٣ ك ١)
ولكن ب ف يعدل المثلث س فالشكل ل ب يعدل المثلث س أيضاً والزاوية غ ب ي تعدل الزاوية ا ب م (ق ١٥ ك ١)
ولكن ي ب غ تعدل الزاوية د فالزاوية ا ب م تعدل د أيضاً فالشكل ل ب قد رسم على الخط المفروض ا ب حتى يعدل المثلث المفروض س والزاوية ا ب م منهُ تعدل الزاوية المفروضة د
فرعٌ. على هذا الاسلوب يتحول مثلث إلى شكلٍ ذي زوايا قائمة مفروض طول ضلع من أضلاعه. لأنه إذا كانت د قائمة و ا ب الضلع المفروض فالشكل ا ب م ل يكون ذا زاويا قائمة ويعدل المثلث المفروض س
القضية الخامسة والأربعون.ع
علينا ان نرسم شكلاً متوازي الأضلاع حتى يعدل شكلاً مفروضاً ذا أضلاع مستقية وزاوية من زواياه تعدل زاوية بسيطة مفروضة
ليكن ا ب س د الشكل المفروض ذا أضلاع مستقيمة و ي الزاوية البسيطة المفروضة فعلينا أن نرسم شكلاً متوازي الأضلاع حتى يعدل ا ب س د وزاوية من زواياه تعدل الزاوية ي
ارسم د ب ثم ارسم الشكل المتوازي الأضلاع ف ح (ق ٤٢ ك ١) حتى يعدل المثلث ا د ب واجعل الزاوية ح ك ف منهُ تعدل الزاوية ي وعلى الخط المستقيم غ ح
ارسم الشكل المتوازي الأضلاع غ م (ق ٤٤ ك ١) واجعلهُ يعدل المثلث د ب س والزاوية غ ح م تعدل الزواية ي
فمن حيث أن الزاوية ي تعدل الزاويتين ف ك ح، غ ح م فالزاوية ف ك ح تعدل غ ح م.
أضف إلى كل واحدة منهما الزاوية غ ح ك فالزاويتان غ ح م، غ ح ك تعدلان الزاويتين ف ك ح، غ ح ك ولكن ف ك ح، ك ح غ معاً تعدلان قائمتين (ق ٢٩ ك ١)
فلذلك ك ح غ، غ ح م تعدلان قائمتين فالخطان ك ح، ح م هما على استقامة واحدة (ق ١٤ ك ١) ومن حيث أن الخط المستقيم غ ح يلاقي المتوازيين ك م، ف غ فالزاويتان المتبادلتان م ح غ، ح غ ف متساويتان (ق ٢٩ ك ١)
أضف إلى كل واحدة منهما الزاوية ح غ ل فالزاويتان م ح غ، ح غ ل تعدلان الزاويتين ح غ ف، ح غ ل تعدلان قائمتين.
فالخطان ف غ، غ ل هما على استقامة واحدة. ومن حيث أن ك ف يوازي ح غ و ح غ يوازي ل م فالخط ك ف يوازي الخط ل م (ق ٣٠ ك ١)
والخط ك م يوازي ف ل فالشكل ك م ل ف متوازي الأضلاع.
والمثلث ا ب د يعدل الشكل ح ف والمثلث د ب س يعدل الشكل غ م فالكل ا ب س د يعدل الكل ك ف ل م.
فقد رُسم شكلٌ متوازي الأضلاع ك م ل ف حتى يعدل الشكل المفروض ا ب س د والزاوية ف ك م منهُ تعدل الزاوية المفروضة ي
فرعٌ. على هذا الأسلوب يبنى على خط مستقيم مفروض شكلٌ متوازي الأضلاع لهُ زاوية تعدل زاوية مفروضة وهو يعدل شكلاً مفروضاً ذا أضلاع مستقيمة، أي يبني أولاً على الخط المفروض شكلاً متوازي الأضلاع يعدل المثلث الأول ا ب د (ق ٤٤ ك ١) وزاوية من زواياهُ تعدل الزاوية المفروضة
القضية السادسة والأربعون.ع
علينا ان نرسم مربعاً على خط مستقيم مفروض
ليكن ا ب الخط المستقيم المفروض. علينا أن نرسم عليهِ مربعاً من النقطة ا ارسم الخط ا س عموداً على ا ب (ق ١١ ك ١)
واقطع ا د حتى يوازي ا ب (ق ٣١ ك ١) ومن ب ارسم ب ي حتى يوازي ا ب (ق ٣١ ك ١) ومن د ارسم د ي حتى يوازي ا د.
فالشكل ا د ي ب متوازي الأضلاع والخط ا ب يعدل د ي والخط ا د يعدل ي ب (ق ٣٤ ك ١) ولكن ا ب يعدل ا د فالخطوط الأربعة ا ب، ا د، د ي، ب ي هي متساوية والشكل المتوازي الأضلاع ا ب ي د هو متساوي الأضلاع أيضاً وزواياهُ قائمة لأن ا د الذي يلاقي المتوازيين د ي، ا ب يجعل الزاويتين ب ا د، ا د ي تعدلان قائمتين (ق ٢٩ ك ١)
وقد جعلت ب ا د قائمة فتكون ا د ي أيضاً قائمة وفي كل شكل ذي أضلاع متوازية تكون الزاويا المتقابلة متساوية (ق ٣٤ ك ١) فالزاويتان ا ب ي، ب ي د هما أيضاً قائمتان فالشكل ذو زوايا قائمة وقد تبرهنت مساواة الأضلاع وقد رُسم على الخط المفروض ا ب
فرعٌ. كل ذي متوازي الأضلاع له قائمة واحدة تكون جميع زواياه قائمات
القضية السابعة والأربعون.ن
في كل مثلثٍ ذي قائمة مربَّعُ الوتر يعدل مربَّعَي الساقين
ليكن ا ب س مثلثاً ذا قائمة ب ا س فمربَّعُ الوتر ب س يعدل مربع ا ب مع مربع ا س
ارسم على ب س المربع ب د ي س (ق ٤٦ ك ١) وعلى ب ا المربع ب غ وعلى ا س المربع س ح ومن ا ارسم ا ل حتى يوازي ب د أو س ي (ق ٣١ ك ١) ارسم ا د و ف س.
الزاوية ب ا س قائمة و ب ا غ كذلك (حدّ ٢٥) فالخط المستقيم ب ا يجعل مع الخطَّين المستقين ا س، ا غ الزاويتين المتواليتين ب ا س، ب ا غ تعدلان قائمتين فالخطان على استقامة واحدة (ق ١٤ ك ١) ولهذا السبب الخطان ب ا، ا ح أيضاً على استقامة واحدة.
والزاوية د ب س تعدل الزاوية ف ب ا لأنهما قائمتان.
أضف إلى كل واحدة ا ب س فكل الزاوية د ب ا تعدل الكل ف ب س (أولية ٢) والضلعان ا ب، ب د يعدلان الضلعين ف ب، ب س كل واحد يعدل نظيره.
والزاوية ا ب د يعدل المثلث ف ب س فالقاعدة ا د تعدل القاعدة ف س (ق ٤ ك ١) والمثلث ا ب د يعدل المثلث ف ب س.
والشكل المتوازي الأضلاع ب ل هو مضاعف المثلث ا ب د (ق ٤١ ك ١) لأنهما على قاعدة واحدة ب د وبين خطين متوازيين ب د، ا ل.
والمربع ب غ هو مضاعف المثلث ف ب س لأنهما على قاعدة واحدة ب ف وبين خطين متوازيين ب ف، غ س والأشياء المضاعفة أشياء متساوية هي متساوية (أولية ٦) فالشكل ب ل يعدل المربع ب غ.
وهكذا إذا رُسم ب ك وأي يبرهن أن الشكل س ل يعدل المربع ح س فكل المربع ب د ي س يعدل المربعين ب غ و ح س
فرعٌ أول. مربعُ ساق مثلثٍ ذي قائمة يعدل مربع الوتر إلا مربع الساق الآخر أي ا ب ٢ = ب س ٢ - ا س ٢
فرع ثان. إذا فرض ا ب = ا س إي إذا كان ا ب س متساوي الساقين فلنا ب س ٢ = ٢ ا ب ٢ = ٢ ا س ٢ و ب س = ا ب √ ٢
فرع ثالث. في مثلثين قائمي الزاويتين إذا عدل ضلعان من الواحد ضلعين من الآخر فالضلع الثالث من الواحد يعدل الثالث من الآخر
القضية الثامنة والأربعون.ن
إذا عدل مربعُ ضلع مثلثٍ مربَّعي الضلعين الآخرين فالمثلث قائم الزاوية
ليكن ا ب س مثلثاً ولنفرض أن مربًّع ب س يعدل مربًّعَي ب ا ا س فتكون ب ا س قائمة
من ا ارسم ا د عموداً على ا س (ق ١١ ك ١) واجعل ا د يعدل ا ب وارسم د س
فمن حيث أن د ا يعدل ا ب فمربع د ا يعدل مربع ا ب أضف إلى كل واحد منها مربع ا س فمربع د ا مع مربع ا س يعدل مربع ب ا مع مربع ا س ولكن مربع د س يعدل مربع د ا مع مربع ا س (ق ٤٧ ك ١) لأن دا س قائمة وحسب المفروض مربع ب س يعدل مربع ب ا مع مربع ا س.
فمربع د س يعدل مربع ب س والضلع د س يعدل الضلع ب س ولأن د ا يعدل ا ب و ا س مشارك بين المثلثين د ا س، ب ا س والقاعدة ب س تعدل القاعدة د س فالزاوية د ا س تعدل الزاوية ب ا س (ق ٨ ك ١) و د ا س قائمة فتكون ب ا س قائمة إيضاً
مضافات إلى الكتاب الأول
قضية ا.ن
الخط العمودي هو أقصر الخطوط التي يمكن رسمها من نقطة خارجة عن خط مفروض إلى ذلك الخط وكل خطَّين مائلين واقعَين على جانبي العمود خارجين من نقطة واحدة وفاصلين جزئين متساويين من الخط الذي يقعان عليه هما متساويان ومن كل خطين أخرين مائلين فاصلين جزئين غير متساويين فابعدهما عن العمود أطولهما ليكن ا ب، ا س، ا د إلى أخرهِ الخطوط المرسومة من النقطة المفروضة ا إلى الخط المستقيم الغير المحدود د ي
وليكن ا ب عموداً فهو أقصر من ا س و ا س أقصر من ا د وهلم جرَّا
لأنَّ الزاوية ا ب س قائمة فالزاوية ا س ب حادَّة (ق ١٧ ك ١) ا ب س والزاوية الصغرى من كل مثلث يقابلها الضلع الاقصر (ق ١٩ ك ١) فالضلع ا ب أقصر من الضلع ا س.
ثم إذا كان ب س و ب ي متساويين يكون الخطان المائلان ا س، ا ي متساويين ايضاً.
لأنَّ الزاوية ا ب س = ا ب ي والضلع ا ب مشترك بين المثلثين ا ب س، ا ب ي فالمثلثان متساويان (ق ٤ ك ١) والضلع ا س = ا ي.
ولأنَّ الزاوية ا س ب حادَّة فالزاوية ا س د منفرجة لإنهما معاً تعدلان قائمتين (ق ١٣ ك ١)
والزاوية ا د س حادَّة لأن ا ب د قائمة فالزاوية ا س د هي أكبر من ا د س فالضلع ا د أطول من الضلع س (ق ١٩ ك ١)
فرعٌ أول. العمود هو قياسٌ حقيقيٌ للبعد بين نقطةٍ وخطٍ لأنهُ البعد الأقرب بينهما
فرعٌ ثانٍ. كل نقطة في عمود على نقطة انتصاف خط هي على بعد واحد من طرفي الخط
فرع ثالث. من نقطة واحدة لا يمكن رسم ثلاثة خطوط متساوية إلى خط واحد وإلا لكان خطان مائلان متساويان على جانب واحد من العمود وذاك لا يمكن
قضية ب.ن
إذا عدل وتر مثلث قائم الزاوية وساق من ساقيه وتر مثلث آخر قائم الزاوية وساقاً من ساقيه فالمثلثان متساويان
لنفرض الوتر ا س = د ف والضلع ا ب = د ي فالمثلث القائم الزاوية ا ب س = القائم الزاوية د ي ف.
فلو فُرِضَتْ مساواة الضلع الثالث منهما لكانت مساواة المثلثين ظاهرة.
وإن لم يكن الضلعان الآخران متساويين فخذ جزءاً من ب س مثل ب ح حتى يعدل ي ف (ق ٣ ك ١)
ارسم ا ح فالمثلث ا ب ح = د ي ف (ق ٤ ك ١)
ارسم ا ح فالمثلث ا ب ح = د ي ف (ق ٤ ك ١)
لأنَّ ا ب = د ي و ب ح = ي ف والزاوية ا ب ح = د ي ف لأنهما قائمتان فلذلك ا ح = د ف
ولكن قد فُرِض أن ا س = د ف فالنتيجة أن ا ح = ا س ولكن حسب القضية الماضية الأبَعد عن العمود هو أطول من الأقراب إليه فلا يمكن أن ا ح = ا س ولا يمكن أن ب س لا يعدل ي ف فالمثلثان ا ب س، د ي ف متساويان
قضية ج.ن
إذا كان ضلعا زاويةٍ موازيين ضلعي زاوية أخرى وكان انفراجهما إلى جهة واحدة فالزاويتان متساويتان
لنفرض أن ا ب يوازي د ف و ا س يوازي د ي فالزاوية س ا ب = ي د ف.
ارسم غ ا د على رأسَيهما. فلأن ا ب يوازي د ف فالزاوية الخارجة غ ا ب = غ د ف (ق ٢٩ ك ١)
ولهذا السبب غ ا س = غ د ي فالبقية س ا ب = البقية ي د ف.
فرعٌ. إذا أُخرج ب ا إلى م و س ا إلى ح فلنا ب ا س = ح ا م وإذ ذاك فالزاوية ح ا م = ي د ف أيضاً
تعليقة. يلزم حصر القضية بشرط انفراج الخطين إلى جهة واحدة لأنَّ في الزاوية س ا م، س ا يوازي ي د و ا م يوازي د ف ولكن الزاويتان غير متساويتين و س ا م و ي د ف معاً تعدلان قائمتين قضية د.ع
مفروض زاويتان من زوايا مثلث وعلينا مثلث وعلينا أن نجد الثالثة
ارسم خطاً مستقيماً مثل س د وفي نقطة منهُ مثل ب أجعل الزاوية س ب ا حتى تعدل واحدة من الزاويتين المفروضتين والزاوية ا ب ي حتى تعدل الاخرى فالباقية ي ب د تعدل الثالثة لان هذه الثلاث زوايا تعدل قائمتين (فرع ق ١٣ ك ١)
قضية ه.ع
مفروض زاويتان من زوايا مثلث وضلع من أضلاعه فعلينا أن نرسم المثلث
الزاويتان المفروضتان تكونان المواليتين ضلع المفروض أو تكون أحداهما متوالية لهُ والاخرى ��تقابلة لهُ. ففي الحالة الثانية استعلم الثالثة حسب القضية الماضية فتكون هي الاخرى المتوالية
ثم ارسم الخط المستقيم ب س حتى يعدل الضلع المفروض وعند ب أجعل الزاوية س ب ا تعدل أحدى المتواليتين وعند س أجعل الزاوية ب س ا تعدل الاخرى المتوالية فالخطان ب ا، ب س يتقاطعان ويحدث من ذلك المثلث المفروض لانه لو كانا متوازيين لكانت الزاويتان عند ب و س تعدلان معاً قائمتين ولم تكونا زوايا مثلث فبالضرورة يكون ا ب س المثلث المطلوب.
قضية و.ع
مفروض ضلعان من أضلاع مثلثٍ وزاويةٌ متقابلة لاحدهما فعلينا أن نرسم المثلث
لهذه العملية حالتان أحداهما متى كانت الزاوية المفروضة منفرجة.
أجعل الزاوية ب ص ا تعدل المفروضة ثم أجعل ص ا يعدل الضلع الذي يوالي الزاوية المفروضة فلو جعلت النقطة ا مركزاً والضلع الاخر أي ا ب بعداً ورُسم قوسٌ لقطع ب س على جانبي ص فلا يمكن أن يرسم أكثر من مثلث واحد ذي زاوية منفرجة على هذه الكيفية وهو المثلث ب ص ا
ولو كانت المفروضة قائمة لرُسِم مثلثان لكن الوتران يقطعان ب س على بعدٍ واحد على جانبي العمود فكان المثلثان متساويين
الحالة الثانية متى كانت الزاوية المفروضة حادَّة والضلع المتقابل أطول من المتوالي فالعمل فيها كما تقدَّم. اجعل ب س ا تعدل المفروضة و ا س يعدل الضلع المتوالي ثم أجعل ا مركزاً والضلع الاخر طولاً فإذا كان طوله ا ب فالقوس يقطع س ب في ب.
ارسم ا ب فيكون ب ا س المثلث المطلوب وإذا كانت المفروضة حادَّة والضلع المتقابل اقصر من الاخر فاجعل ا مركزاً و ا س بعداً فالقوس يقطع ب س في س و ص على جانب واحد من ب فيحدث مثلثان ب ا ص، ب ا س وكل واحد منهما مستوفٍ شروط العمل.
تعليقة. في هذه الحالة الاخيرة لو كان طول الضلع الأقصر طول العمود من ا إلى ب س لحدث مثلثٌ قائم الزاوية. ولو كان ذلك الضلع أقصر من العمود من ا على ب س لكانت المسئلة غير ممكنة في كل الأحوال
قضية ز.ع
علينا أن نجد مثلثاً يعدل شكلاً مفروضاً ذا أضلاعٍ مستقيمة
ليكن ا ب س د ي الشكل المفروض. ارسم القطر س ي الذي يفصل من الشكل المثلث س د ي. ارسم د ف حتى يوازي س ي واخرج ا ي إلى ف ثم أرسم س ف فالشكل ا ب س د ي يعدل الشكل ا ب س ف لانَّ المثلثين س د ي س ف ي هما على قاعدة واحدة س ي وبين خطين متوازيين س ي د ف فهما متساويان (ق ٣٧ ك ١)
ثم ارسم القطر س ا وارسم ب غ حتى يوازي س ا واخرج ي ا إلى غ وارسم س غ فالشكل ا ب س د ي قد تحول إلى مثلث يعدله غ س ف
فرع. من حيث أن المثلث يمكن تحزيلهُ إلى شكل ذي زوايا قائمة يعدله فبالضرورة كل ذي أضلاع كثيرة يمكن تحويله إلى شكل ذي زوايا قائمة يعدله
قضية ح.ع
علينا أن نستعلم ضلع مربعٍ يعدل مجتمع مربعين
ارسم خطين غير محدودين مثل ا ب، ا س أحدهما عمودي على الآخر. ثم أقطع ا ب حتى يعدل ضلعاً من احد المربعين المفروضين و ا س الاخر.
أرسم ب س فلان ب ا س قائمة فمربع ب س = مربع ب ا مع مربع ا س (ق ٤٧ ك ١)
تعليقة. هكذا يُرسَم مربعٌ يعدل مجتمع أيّ مربعات فُرضت وذلك بتحويل ثلاثة منها إلى اثنين واثنين إلى واحد وهلمَّ جرَّا.
قضية ط.ع
علينا أن نجد ضلع مربعٍ يعدل فضلة مربعين مفروضين
ارسم كما في القضية السابقة ا س، ا د أحدهما عموداً على الآخر واجعل ا س يعدل ضلع أصغر المربعين ثم أجعل س مركزاً وضلع المربع الآخر بعداً وارسم قوساً يقطع ا د في د فالمربع المرسوم على ا د يعدل فضلة مربَّعي س د و ا س لأن د ا س قائمة و ا د2 = س د2 - ا س2 (ق ٤٦ ك ١ فرع أول)
قضية ي.ع
مفروض شكلٌ ذو زوايا قائمة وعلينا أن نرسم أخر مثلهُ لهُ ضلع مفروض
ليكن ا ي، ق ح الشكل المفروض.
اخرج ضلعاً من أضلاعهِ مثل ا ح حتى يصير ح ب على الطول المفروض.
أخرج ا ي وارسم ب ق وأجعل ق غ يعدل ح ب وارسم ب غ س و ح ق ك حتى يوازيا ا ب أو ي غ
فالشكل غ ق ك س يعدل ا ح ق ي (ق ٤٣ ك ١) ولهُ ق غ الضلع المفروض
فرعٌ. شكل ذو أضلاع كثيرة يمكن تحويلهٌ إلى شكل ذي زوايا قائمة يعدلهٌ ولهٌ ضلع مفروض
