قطع مخروطي

1. قطع مكافئ
2. دائرة وقطع ناقص
3. قطع زائد
في الرياضيات وبالتحديد في الهندسة الوصف��ة، القطع المخروطي هو منحنى ناتج عن تقاطع مخروط مستو لا يمر برأس وغير متماس له (التقاطع في هاتين الحالتين نقطة أو مستقيم).
دُرست القطع المخروطية منذ وقت طويل يعود إلى 200 قبل الميلاد عندما قام أبلونيوس البرغاوي بإجراء دراسة تبين خصائصها.
الهندسة الإقليدية
[عدل]التعريف التحليلي
[عدل]في التحليل الرياضي القطع المخروطي هو المحل الهندسي لنقطة تتحرك بحيث تكون العلاقةُ بينَ بعدها عن نقطةٍ ثابتةٍ وبعدها عن مستقيمٍ ثابتٍ نسبةً ثابتةً. تسمى هذه النسبة الاختلاف المركزي (Eccentricity)، كما تسمى النقطة الثابتة البؤرة (Focus)، أما المستقيم الثابت فيسمى الدليل (directrix).
حيث:
- P هي نقطة (x,y) تقع على القطع.
- S البؤرة
- e معامل الاختلاف المركزي
- و m هي مسقط العمودي ل P على الدليل.
إذا كان الاختلاف المركزي مساويا للوحدة (يساوي الواحد) سُمِّيَ المنحنى قطعًا مكافئًا (Parabola)، وإذا كان الاختلاف المركزي أقل من الوحدة سمي المنحنى قطعا ناقصا (Ellipse)، وإذا كان الاختلاف المركزي أكبر من الوحدة سمي المنحنى قطعا زائدا (Hyperbola).
وتسمى القطوع المكافئة والناقصة والزائدة بالقطوع المخروطية، لأنه يمكن أن تتولد نتيجة قطع السطح المخروطي بمستو في وضع معين.
أنواع القطوع المخروطية
[عدل]لها ثلاثة أنواع هي القطع المكافئ (شلجم)، القطع الزائد (هذلول)، والقطع الناقص (إهليلج). وقد تُعدُّ الدائرة نوعًا رابعًا (كما عدَّها أبولونيوس) أو يمكن عدُّها نوعا من القطوع الناقصة (عندما يكون المحوران متساويان). ويتشكل القطع الناقص والدائرة عندما يكون تقاطع المستوى والمخروط منحنى مغلق. وتتشكل الدائرة عندما يكون المستوى القاطع موازيًا لدائرة القاعدة المولدة للمخروط (وفي هذه الحالة يسمى مخروط دائري). بالنسبة لمخروط يميني (كما في الشكل المقابل في أعلى الصورة) يكون المستوى القاطع عموديًا على محور تماثل المخروط. إذا كان المستوى القاطع موازيا لخط واحد فقط من الخطوط المولدة للمخروط حينها يصبح القطع مفتوحًا وليس مغلقًا فيسمى قطعًا مكافئًا. وفي الحالة الأخيرة يتكون القطع الزائد وعندما يكون المستوى موازي لراسمين من رواسم المخروط وبالتالي يقطع كلا الطيتين، مكونًا بذلك منحنيين منفصلين ومفتوحين، يتم أحيانا تجاهل أحدهما والعمل بالآخر.
حالات شاذة
[عدل]توجد حالات شاذة تنتج عندما يمر المستوى القاطع برأس المخروط Apex. التقاطع في هذه الحالات قد يكون خطًا مستقيما (إذا كان المستوى مماسًا لسطح المخروط)؛ أو نقطة (إذا كانت الزاوية بين المستوى ومحور المخروط أكبر من المماس)؛ أو زوجا من الخطوط المتقاطعة (عندما تكون الزاوية أصغر).
عندما يصبح المخروط أسطوانة أي عندما يكون الرأس واقعا في منطقة اللانهاية تنتج قطوع أسطوانية. بالرغم من أن ذلك يتسبب غالبًا في قطع ناقص أو دائرة، إلا أن هناك حالة شاذة تنتج خط أو خطين متوازيين عندما يكون مستوى القطع، بالتوالي، متماس للأسطوانة أو قاطعا لها (بشرط أن يكون موازي لراسم من رواسمها)
الاختلاف المركزي
[عدل]- انظر أيضاً: لا مركزية (رياضيات)

شروط التعريف الأربعة الواردة أعلاه يمكن جمعها في شرط واحد يعتمد على نقطة افتراضية F (البؤرة) ومستقيم L (الدليل) لا يمر بالنقطة F وعدد حقيقي غير سالب e (هو معامل الاختلاف المركزي). القطع المخروطي المقابل يتكون من جميع النقاط التي تبعد عن F مسافةً تساوي e مرة بعدها عن L. إذا كانت e بين 0 و 1 نحصل على قطع ناقص، إذا كانت e=1 نتحصل على قطع مكافئ وإذا كانت أكبر من 1 نحصل على قطع زائد.
يوجد دليلان وبؤرتان لكل من القطع الزائد والناقص. المسافة من المركز إلى الدليل هي ، بينما هو نصف المحور الأكبر للقطع الناقص، أو المسافة من المركز إلى قمة القطع الزائد. المسافة من المركز للبؤرة هي .
في حالة الدائرة يكون معامل الاختلاف المركزي e= 0 ويمكن تخيل أن الدليل قد اُسْتُبْعِد لانهائيًا عن المركز. لكن من غير المفيد استخدام التعبير: إن الدائرة تتكون من كل النقاط التي التي تبعد مسافة e مرة بعدها عن L لأننا سنحصل على 0 مضروبة في مالانهاية.
لذلك فإن المميز الأساسي ما يخص القطع المخروطي هو مقياس يبين لأي مدى يبعد القطع عن أن يكون دائرة. لقيمة معطا�� ، كلما اقتربت من 1 كلما نقص طول نصف المحور والأصغر.
محددات القطع
[عدل]
بالإضافة إلى الاختلاف المركزي (e)، والبؤر، والدليل، ترتبط العديد من الميزات والأطوال الهندسية بقطع مخروطي.
المحور الرئيسي: هو المستقيم الذي يشمل بؤر القطع الناقص أو القطع الزائد، ومركزها هي مركز المنحنى. القطع المكافئ ليس له مركز.
الاختلاف المركزي الخطي c (بالإنجليزية: Linear eccentricity) هي المسافة بين المركز والبؤرة.
الوتر العمودي البؤري (باللاتينية: latus rectum) الوتر الموازي للدليل ويمر عبر البؤرة؛ نصف طوله هو نصف الوتر العمودي البؤري (ℓ).
المحدد البؤري p (بالإنجليزية: Focal parameter) هو المسافة بين البؤرة المقابلة.
المحور الأكبر (بالإنجليزية: Major axis) هو الوتر بين الرأسين: أطول وتر للقطع الناقص، وأقصر وتر بين فرعَيْ القطع الزائد، يطلق على نصف طوله اسم نصف المحور الأكبر a
المحور الأصغر (بالإنجليزية: Minor axis) هو أقصر قطر للقطع الناقص، ونصف طوله يطلق عليه نصف المحور الأصغر b، نفس القيمة b كما في المعادلة القياسية أدناه. على سبيل القياس، بالنسبة للقطع الزائد، نسمي أيضًا المعلمة b في المعادلة القياسية، شبه المحور الأصغر.
فيما يلي علاقة بعض المحددات المذكورة أعلاه بالاختلاف المركزي:[1]
بالنسبة القطوع المخروطية في الوضع القياسي، فإن هذه المحددات لها القيم التالية، مع أخذ .
| قطع مخروطي | معادلة | الاختلاف المركزي (e) | الاختلاف المركزي الخطي (c) | نصف الوتر العمودي البؤري (ℓ) | محدد بؤري (p) |
|---|---|---|---|---|---|
| دائرة | |||||
| قطع ناقص | |||||
| قطع مكافئ | غير موجود | ||||
| قطع زائد |
المعادلة الجبرية
[عدل]يمكن تمثيل معادلة القطع المخروطي بأشكال مختلفة منها:
- إذا كان الاختلاف المركزي يساوي ھ وكانت البؤرة عند نقطة الأصل (0,0) والدليل مستقيما عموديا على محور السينات يقطعه على بعد ف فإن معادلة القطع المخروطي تعطى بالمعادلة التالية:
(1 - ھ^2) س^2 + 2ھ^2 ف س + ص^2 = ھ^2 ف
- معادلة من الدرجة الثانية في متغيرين س، ص ويمكن كتابة هذه المعادلة على الصورة التالية:
أ س^2 + 2ب س ص + جـ ص^2 + 2د س + 2ھ ص + و = 0
الإحداثيات الديكارتية
[عدل]في النظام الإحداثي الديكارتي يكون منحنى دالة تربيعية في متغيرين دوما قطعا مخروطيا، وكل القطوع المخروطية تتكون بهذه الطريقة. معادلتها تكون في الصورة:
- حيث , , ليسوا جميعًا أًصفارًا.
نحسب المميّز لمعرفة نوع القطع.
- إذا كان ، نحصل على معادلة قطع ناقص (مالم يكن المخروط منحلا، مثلًا )؛
- إذا كان و المعادلة تمثل دائرة؛
- إذا كان ، نحصل على معادلة قطع مكافئ.
- إذا كان ، نحصل على معادلة قطع زائد.
- أيضاًإذا كان ، نحصل على معادلة قطع زائد قائم.
لاحظ أن A و B هي معاملات لا تمثل أي أطوال للمحاور الأكبر والأصغر كما سيتم تعريفها في القسم التالي
في تعبير المصفوفات تصبح المعادلات السابقة كالتالي:
أو
و
- .
رغم تغيير الإحداثيات يمكن وضع هذه المعادلات في صورة قياسية:
- الدائرة:
- القطع الناقص:
- القطع المكافئ:,
- القطع الزائد:
- القطع الزائد القائم:
مثل هذه الصيغ تكون متماثلة حول محور x، وفيما يخصُّ الدائرة والقطع الزائد والناقص حول محور y و القطع الزائد القائم هي حالة التماثل الوحيدة التي تكون حول و. لذلك فان دالتها العكسية هي نفس الدالة الأصلية.
يمكن كتابة هذه الصيغ القياسية في صورة معادلات وسيطية (بارامترية):
- الدائرة:
- القطع الناقص:
- القطع المكافئ:
- القطع الزائد: أو
- القطع الزائد القائم:
الإحداثيات المتجانسة
[عدل]في الإحداثيات المتجانسة، القطع المخروطي يمكن تمثيلها كالتالي:
أو بتعبير المصفوفات:
المصفوفة تدعى «مصفوفة القطع المخروطي». تدعى محددة القطع المخروطي. إذا كان Δ = 0 فإن القطع المخروطي يسمى «منحلًا Degenerate»، وهذا يعني أنه في الحقيقة عبارة عن اتحاد خطين مستقيمين. أي قطع مخروطي يتقاطع مع نفسه هو قطع منحلة، ولكن ليس كل القطوع المنحلة تقاطع نفسها، وفي هذه الحالة يكون القطع خطًا مستقيماً.
على سبيل المثال القطع المخروطي
- يختزل اتحاد المستقيمين:
- .
وبالمثل يختزل القطع المخروطي أحيانًا خطًا مفردا:
- .
يدعى مميز القطع المخروطي. إذا كان δ == 0 فالقطع المخروطي مكافئ، إذا كان δ<0 فهو زائد، واذا كان δ>0 فهو ناقص. إذا كان δ>0 و A1 = A2 فهي دائرة، أما إذا كان δ<0 و A1 == -A2 فهو قطع زائد قائم. يمكن اثبات أنه في مستوى الإسقاط المركب CP2 قطعين مخروطيين بينهما 4 نقاط مشتركة (إذا أخذنا في الاعتبار التعددية Multiplicity) أي لا يوجد أكثر من 4 نقاط تقاطع وتوجد دائمًا نقطة تقاطع واحدة (الاحتمالات: 4 نقاط تقاطع مختلفة، أو نقطتي تقاطع فرديتين ونقطة تقاطع مزدوج، أو نقطتي تقاطع مزدوج، أو نقطة تقاطع فردي ونقطة تقاطع بتعددية 3، أو نقطة تقاطع واحدة بتعددية 4). إذا وجدت نقطة تقاطع واحدة على الأقل ذات تعددية > 1 يقال أن القطعين المخروطيين متماسين. أما إذا كان هناك نقطة تقاطع واحدة ذات تعددية 4 يقال أن القطعين متلامسين osculating.
إضافة لما سبق فإن كل خط مستقيم يقاطع كل من القطعين المخروطيين مرتين. إذا كانت نقطة التقاطع مزدوجة عُدَّ الخط مماسًا ويسمى المماس. لأن كل مستقيم يقاطع القطع مرتين فإن كلا القطعين المخروطيين له نقطتين في مالانهاية (تقاطع النقاط مع خط المالانهاية) فإذا كانت النقطتان حقيقيتان فلابد أن يكون القطع زائدًا، وإذا كانتا تخيليتين فلابد أن يكون القطع ناقصًا، أما إذا كان للقطع نقطة واحدة مزدوجة في مالانهاية فهو مكافئ.
تطبيقات
[عدل]انظر إلى تطبيقات الدائرة والقطع الناقص والقطع المكافئ والقطع الزائد.
التاريخ
[عدل]مينايخموس والأعمال القديمة
[عدل]يعتقد أن التعريف الأول لقطع مخروطي قدمه مينايخموس (توفي 320 قبل الميلاد) كجزء من حله لمعضلة ديلية (مضاعفة المكعب).[2][3] لم ينجُ عمله، ولا حتى الأسماء التي استخدمها لهذه المنحنيات، وهو معروف فقط من خلال الحسابات الثانوية.[4] يختلف التعريف المستخدم في ذلك الوقت عن التعريف المستخدم اليوم. أنشئت المخاريط من خلال تدوير مثلث قائم حول أحد ساقيه، لذا فإن الوتر يولد سطح المخروط (يسمى هذا الخط مولد السطح). حُدِّدت ثلاثة أنواع من المخاريط من خلال زوايا قمة الرأس (تقاس ضعف الزاوية التي شكلها وتر المثلث والساق التي تدور حولها في المثلث القائم). ثم حُدِّد القطع المخروطي عن طريق تقاطع أحد هذه المخاريط مع مستوي مرسوم عموديًا على المولد. يتم تحديد نوع القطع من خلال نوع المخروط، أي من خلال الزاوية المتشكلة في قمة المخروط: إذا كانت الزاوية حادة، فإن القطع عبارة عن قطع ناقص؛ إذا كانت الزاوية قائمة، فإن القطع عبارة عن قطع مكافئ؛ وإذا كانت الزاوية منفرجة، فإن المخروط عبارة عن قطع زائد (ولكن فقط فرع واحد من المنحنى).[5]
يقال أن إقليدس (حوالي 300 قبل الميلاد) كتب أربعة كتب عن المخاريط ولكن فقدت أيضًا.[6] ومن المعروف أن أرخميدس (توفي عام 212 ق.م) درس القطوع المخروطية، بعد أن حدد مساحة المنطقة التي يحدها القطع المكافئ والوتر في كتابه «تربيع القطع المكافئ». كان اهتمامه الرئيسي يتعلق بقياس مساحات وحجوم الأشكال المتعلقة بالقطوع وبقي جزء من هذا العمل على قيد الحياة في كتابه عن المجسمات الدورانية للقطوع المخروطية «عن أشباه المخروط والسطوح الكروية».[7]
أبلونيوس البرغاوي
[عدل]
يرجع أعظم تقدم في دراسة المخاريط من قبل الإغريق إلى أبلونيوس البرغاوي (توفي عام 190 ق.م)، الذي تلخص كتابه عن المخاريط المكونة من ثمانية مجلدات وتوسِّع المعرفة الموجودة إلى حد كبير.[8] جعلت دراسة أبلونيوس لخصائص هذه المنحنيات من الممكن إظهار أن أي مستوي يقطع مخروطًا مزدوجًا ثابتًا، بغض النظر عن الزاوية، ستنتج مخروطًا وفقًا للتعريف القديم، مما يؤدي إلى التعريف المستخدم بشكل شائع اليوم. كما يمكن الحصول على الدوائر غير القابلة للإنشاء بالطريقة القديمة بهذه الطريقة. قد يكون هذا سبب لماذا اعتبر أبلونيوس الدوائر نوعًا رابعًا من القطع المخروطي، وهو تمييز لم يعد يتم إجراؤه. استخدم أبلونيوس الأسماء التالية لهذه المنحنيات: ellipse ، و parabola و hyperbola ، واستعار المصطلحات من أعمال فيثاغورس السابقة حول المساحات.[9]
يعود الفضل إلى ببس الرومي (توفي عام 350 م) في شرح أهمية مفهوم بؤرة القطع، وتفصيل مفهوم ذي الصلة بالدليل (Directrix)، بما في ذلك حالة القطع المكافئ (الذي يفتقر إليه أعمال أبلونيوس المعروفة).[10]
القوهي
[عدل]تم وصف أداة لرسم القطوع المخروطية لأول مرة عام 1000 م من قبل عالم الرياضيات المسلم أبو سهل القوهي.[11][12]
عمر الخيام
[عدل]تُرجِمت أعمال أبلونيوس إلى اللغة العربية، ولم يبق الكثير من أعماله إلا النسخة العربية. وجد العلماء المسلمين تطبيقات النظرية، أبرزها عالم الرياضيات والشاعر المسلم عمر الخيام، الذي استخدم قطوعًا مخروطية لحل المعادلات الجبرية التي لا تزيد عن ثلاث درجات.[13][14]
أوروبا
[عدل]مدّد يوهانس كيبلر نظرية القطوع المخروطية من خلال «مبدأ الاستمرارية»، مقدمة لمفهوم النهايات. استخدم كيبلر مصطلح foci «البؤر» لأول مرة عام 1604.
طور جيرار ديزارغ وبليز باسكال نظرية القطوع المخروطية باستخدام شكل قديم للهندسة الإسقاطية، مما ساعد على توفير الدفع لدراسة هذا المجال الجديد. على وجه الخصوص، اكتشف باسكال مبرهنة تُعرف باسم hexagrammum mysticum والتي يمكن من خلالها استنتاج العديد من الخصائص الأخرى للقطوع المخروطية.[15]
قام كل من رينيه ديكارت وبيير فيرمات بتطبيق الهندسة التحليلية المكتشفة حديثًا على دراسة المخروطيات. كان لهذا تأثير الحد من المشاكل الهندسية للمخروطيات إلى مشاكل في الجبر. ومع ذلك، كان جون واليس في كتابه 1655 أطروحة Tractatus de sectionibus conicis هو الذي عرّف أولاً القطوع المخروطية على أنها نماذج لمعادلات من الدرجة الثانية.[16] كُتِب في وقت سابق، ولكن تم نشره لاحقًا، يبدأ الكتاب Elementa Curvarum Linearum ليوهان دي فيت بإنشاء كيبلر الكينيماتيكي للقطوع ثم تطوير المعادلات الجبرية. وُصِف هذا العمل، الذي يستخدم منهجية فيرما وتدوين ديكارت بأنه أول كتاب حول هذا الموضوع.[17] صاغ دي فيت مصطلح Directrix.[17]
معرض
[عدل]-
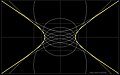
تحول زائدي لقطع ناقص. الذي يمكن أن تكون دالة سطح من الدرجة الثانية (ناقص، مكافئ ، زائد)[18]
-
معلوم: مخروطيتين متماستين، مطلوب: تحديد المخروط الذي يمر بهما.
-
تحديد الأنواع الثلاثة من المخروطيات (قطع ناقص ومكافئ وزائد) بحيث تتماس في نقطة عامة (غير محورية) باستخدام إجراءات هندسية وصفية.
-
تقريب منحنى تكعيبي باستخدام قطوع مخروطية
انظر أيضًا
[عدل]مراجع
[عدل]- ^ Brannan, Esplen & Gray 1999، صفحات 13–16
- ^ According to فلوطرخس this solution was rejected by Plato on the grounds that it could not be achieved using only straightedge and compass, however this interpretation of Plutarch's statement has come under criticism.Boyer 2004، p.14, footnote 14
- ^ Boyer 2004، صفحات 17–18
- ^ Boyer 2004، صفحة 18
- ^ Katz 1998، صفحة 117
- ^ Heath, T.L., The Thirteen Books of Euclid's Elements, Vol. I, Dover, 1956, pg.16
- ^ Eves 1963، صفحة 28
- ^ Apollonius of Perga, Treatise on Conic Sections, edited by توماس ليتل هيث (Cambridge: Cambridge University Press, 2013). نسخة محفوظة 19 يونيو 2020 على موقع واي باك مشين.
- ^ Eves 1963، صفحة 30
- ^ Boyer 2004، صفحة 36
- ^ Stillwell، John (2010). Mathematics and its history (ط. 3rd). New York: Springer. ص. 30. ISBN:978-1-4419-6052-8.
- ^ "Apollonius of Perga Conics Books One to Seven" (PDF). مؤرشف من الأصل (PDF) في 2013-05-17. اطلع عليه بتاريخ 2011-06-10.
- ^ Boyer, C. B., & Merzbach, U. C. , A History of Mathematics (Hoboken: John Wiley & Sons, Inc., 1968), p. 219. نسخة محفوظة 30 يونيو 2019 على موقع واي باك مشين.
- ^ Van der Waerden, B. L. , Geometry and Algebra in Ancient Civilizations (برلين/هايدلبرغ: Springer Verlag, 1983), p. 73. نسخة محفوظة 2018-12-04 على موقع واي باك مشين.
- ^ Katz 1998، صفحة 126
- ^ Boyer 2004، صفحة 110
- ^ ا ب Boyer 2004، صفحة 114
- ^ د. حسن العيسوي. نمذجة وصفية نسخة محفوظة 2023-01-31 على موقع واي باك مشين.
مصادر
[عدل]- معجم الرياضيات - تأليف لجنة من الخبراء من وزارة التربية والتعليم - عمان - طبعة مكتبة لبنان - ساحة رياض الصلح/ بيروت - 1980م.
روابط خارجية
[عدل]- إذا علم مخروط قائم ومستوى قاطع له وكان المطلوب إيجاد مسقطي تقاطعهما. الهندسة الوصفية. إبراهيم افندي