Konstruktiewe ruimtemeetkunde

Konstruktiewe ruimtemeetkunde (KRM), beter bekend onder die Engelse naam Constructive Solid Geometry (CSG), is 'n geometriese modelleermetode. Dit dien as metode om komplekse meetkundige liggame te definieer uit 'n kombinasie van eenvoudiger liggame. Dit is 'n prosedurele modelleertegniek wat in rekenaargrafika en rekenaargesteunde ontwerp gebruik word.

Die eenvoudige liggame waaruit die komplekser liggame opgebou word, word primitiewes genoem. Dit is oor die algemeen liggame met 'n eenvoudige vorm: blokke, silinders, prismas, piramides, bolle en keëls. Die versameling toegestane primitiewes kan beperk word, byvoorbeeld gebuigde oppervlakke kan verbied word.

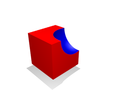
So 'n primitiewe word gesien as 'n versameling van (oneindig baie) punte in die ruimte. Gestel 'n voorwerp word opgebou uit primitiewes deur middel van toegestane bewerkinge wat normale boolse bewerkinge op die versameling punte is: vereniging, snyding en verskil.

In modelleerpakkette is eenvoudige meetkundige voorwerpe soos die kubus, blok, bol, torus en andere voorwerpe wat deur wiskundige formules beskryf kan word, beskikbaar as primitiewes. Hierdie voorwerpe kan normaalgesproke beskryf word deur 'n prosedure wat 'n aantal parameters insluit. Byvoorbeeld, 'n bol kan beskryf word deur die koördinate van die middelpunt gekombineer met 'n straal. Hierdie primitiewes kan gekombineer word tot saamgestelde liggame deur bewerkinge as volg:

Bewerkinge in konstruktiewe ruimtemeetkunde

Boolse vereniging	Boolse verskil	Boolse snyding
Saamvoeging van twee voorwerpe tot een.	Twee voorwerpe van mekaar afgetrek.	Die ruimte wat tot beide primitiewes behoort.

By uitvoering van KRM-bewerkinge ontstaan gereeld bengelende of geïsoleerde syvlakke, sye en hoekpunte. Dit kan byvoorbeeld gebeur deur twee kubusse presies teen mekaar aan te lê en hier die deursnee daarvan te neem, die raaklyn behoort tot beide voorwerpe.

Vanweë rekenkundige akkuraatheid sal daar bowendien altyd 'n bepaalde randgebied wees waarin dit onseker is of 'n punt binne of buite 'n liggaam val. Dit word opgelos deur in plaas van wiskundige bewerkinge, gereelde versamelingsbewerkinge te gebruik. Hiervoor definieer ons die volgende:

• 'n Punt is deel van 'n liggaam as dit moontlik is om 'n bolletjie met 'n oneindig, klein straal om dié punt heen te neem wat volledig binne die liggaam se grense lê.
• 'n Punt lê op die grens van 'n liggaam as enig sodanig gedefinieerde punte (sien hierbo) 'n element van die liggaam bevat.

Die gereelde versamelingsbewerkinge gee die deel van die liggaam gekonstrueer deur die bybehorende wiskundige versamelingsbewerkinge, wat aan beide kriteria voldoen.

In die praktyk sal mens die kriteria benader, byvoorbeeld in plaas van 'n oneindig klein straal sal mens 'n baie klein straal van die bolletjie neem.

'n Liggaam wat saamgestel is met KRM kan in rekenaargeheue voorgestel word deur die voorstelling van die afsonderlike primitiewes, plus 'n boolse uitdrukking. Dikwels word die operatore +, * en - gebruik vir respektiewelik vereniging, snyding en verskil. 'n Voorbeeld van so 'n uitdrukking is:

(a+b)*c

... wat beteken dat die primitiewes a en b verenig word waarna die snyding met c geneem word. Hoe die primitiewes a, b en c voorgestel word is vir KRM self nie belangrik nie.

Intern in programme word 'n dergelike uitdrukking dikwels bygehou in die vorm van 'n sogenaamde KRM-boom. Dit is 'n binêre boom wat die uitdrukking weergee. Vir die bogenoemde voorbeeld sou so 'n boom as volg daar uitsien:

    /*\
   /   \
  /+\   c
 /   \
a     b

...wat wederom beteken dat a en b verenig word, waarna die resultaat se snyding met c geneem word.

Konstruktiewe ruimtemeetkunde het 'n aantal praktiese toepassinge. Deurdat die wiskunde van die afsonderlike voorwerpe eenvoudig gehou word, bly die programmatiese kompleksiteit om KRM te implementeer binne perke. Desondanks is dit moontlik om komplekse voorwerpe baie suksesvol te modelleer met KRM, selfs as die hoeveelheid primitiewes beperk is. KRM is dan ook 'n populêre ontwerpmetode in rekenaargesteunde ontwerp en word graag in rekenaargrafika gebruik as voorstelling van voorwerpe wat weergegee moet word. Selfs in rekenaarspelletjies word dit gebruik - die 3d-enjin van die spelletjie Unreal maak byvoorbeeld hiervan gebruik.