Сітка Аполлонія

Сітка Аполлонія
Названо на честь	Аполлоній Перзький
Наступник	Apollonian sphere packingd
Підтримується Вікіпроєктом	Вікіпедія:Проєкт:Математика
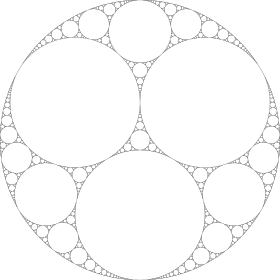
Сітка Аполлонія у Вікісховищі

Сітка Аполлонія — фрактал, що будується за трьома колами, які попарно дотикаються. Являє собою граничну множину різноманітних послідовностей кіл, кожна з яких дотикається до трьох вже побудованих. Названа на честь грецького математика Аполлонія Перзького.

Почнемо з трьох кіл, кожне з яких є дотичним до двох інших. Далі рекурсивно додамо до наявної фігури кола, кожне з яких дотикається будь-яких трьох вже побудованих кіл. На першому кроці ми додамо два, на другому шість і так далі.

Продовжуючи побудову, ми додаємо 2·3ⁿ нових кіл на n-ому кроці.

Замикання побудованих кіл називається сіткою Аполлонія.

• Сітка Аполлонія має розмірність Гаусдорфа близько 1,3057^[1].
• Сітку Аполлонія можна подати як об'єднання двох підмножин, гомеоморфних трикутнику Серпінського, зі спільними вершинами.
• Підгрупа групи перетворень Мебіуса, що складається з таких перетворень, які переводять сітку Аполлонія в себе, діє транзитивно на колах сітки.
• Сітку Аполлонія можна визначити як граничну множину групи перетворень площини утвореної інверсіями в чотирьох попарно дотичних колах.

Кривина кола визначається як обернене до його радіусу.

• Від'ємна кривина вказує на те, що всі інші кола дотикаються до цього кола зсередини. Це обмежувальне коло.
• Нульова кривина дає пряму (коло з нескінченним радіусом).
• Додатна кривина вказує на те, що всі інші кола дотикаються до цього кола зовні. Це коло знаходиться всередині кола з від'ємною кривиною.

В сітці Аполлонія всі кола мають додатну кривину, крім одного, обмежувального кола.

Нехай ${\displaystyle a,b,c,d}$ позначають кривини чотирьох попарно дотичних кіл. За теоремою Декарта:

${\displaystyle a^{2}+b^{2}+c^{2}+d^{2}={\tfrac {1}{2}}\cdot (a+b+c+d)^{2}}$

Звідси випливає, що якщо чотири кола, що попарно дотикаються, мають цілі кривини, то й всі інші кола в їх сітці Аполлонія мають цілі кривини. Є нескінченно багато таких цілих сіток. ^[2] Нижче наведено декілька цілих сіток з позначеними кривинами кіл.

• Тривимірний еквівалент сітки Аполлонія - Аполлонієве пакування сфер.

• Фрактальна графіка
• Фрактальна геометрія