Параболоїд

Параболоїд
Формула	${\displaystyle {\frac {z}{c}}={\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}}$
Підтримується Вікіпроєктом	Вікіпедія:Проєкт:Математика
Параболоїд у Вікісховищі

Параболо́їд — тип поверхні другого порядку.

Канонічне рівняння параболоїда в декартових координатах:

${\displaystyle ~z=ax^{2}+by^{2}}$

• якщо ${\displaystyle a}$ і ${\displaystyle b}$ мають один знак, то параболоїд зветься еліптичним.
• якщо ${\displaystyle a}$ і ${\displaystyle b}$ мають різні знаки, то параболоїд зветься гіперболічним.
• якщо один з коефіцієнтів дорівнює нулю, то параболоїд зветься параболічним циліндром.

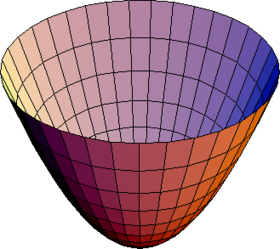
Еліптичний параболоїд виглядає як овальна чашка й може мати точку максимуму або мінімуму. У системі координат з трьома осями ${\displaystyle x}$, ${\displaystyle y}$ і ${\displaystyle z}$, еліптичний параболоїд може бути поданий рівнянням

${\displaystyle z={\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}.}$

де ${\displaystyle a}$ і ${\displaystyle b}$ — константи, що визначають кривизну в площинах ${\displaystyle x}$-${\displaystyle z}$ і ${\displaystyle y}$-${\displaystyle z}$ відповідно.

Гіперболічний параболоїд (не плутати з гіперболоїдом) — це двічі лінійчата поверхня, що має вигляд сідла. У підходящій системі координат гіперболічний параболоїд може бути поданий рівнянням

${\displaystyle z={\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}.}$

Гіперболічний параболоїд — це двічі лінійчата поверхня, тому може бути використана для побудови сідлової поверхні з ліній.

Коли a = b, еліптичний параболоїд перетворюється на параболоїд обертання: поверхню отримано обертанням параболи навколо її осі. Форму параболоїду обертання мають параболічні рефлектори, дзеркала, антенні тарілки тощо. Форма рідини, що обертається в рідинно-дзеркальних телескопах, також є параболоїдом обертання. Параболоїд обертання також називається круговим параболоїдом.

Еліптичний параболоїд, що параметризований як

${\displaystyle {\vec {\sigma }}(u,v)=\left(u,v,{u^{2} \over a^{2}}+{v^{2} \over b^{2}}\right)}$

має Ґаусову кривину

${\displaystyle K(u,v)={4 \over a^{2}b^{2}\left(1+{4u^{2} \over a^{4}}+{4v^{2} \over b^{4}}\right)^{2}}}$

і середню кривину

${\displaystyle H(u,v)={a^{2}+b^{2}+{4u^{2} \over a^{2}}+{4v^{2} \over b^{2}} \over a^{2}b^{2}\left(1+{4u^{2} \over a^{4}}+{4v^{2} \over b^{4}}\right)^{3/2}}}$

обидві з яких є позитивними, мають максимум на початку відліку, стають меншими з рухом точки від початку відліку, прямують асимптотично до нуля, коли точка рухається нескінченно віддалено від початку відліку.

Гіперболічний параболоїд параметризований як

${\displaystyle {\vec {\sigma }}(u,v)=\left(u,v,{u^{2} \over a^{2}}-{v^{2} \over b^{2}}\right)}$

має Ґаусову кривину

${\displaystyle K(u,v)={-4 \over a^{2}b^{2}\left(1+{4u^{2} \over a^{4}}+{4v^{2} \over b^{4}}\right)^{2}}}$

і середню кривину

${\displaystyle H(u,v)={-a^{2}+b^{2}-{4u^{2} \over a^{2}}+{4v^{2} \over b^{2}} \over a^{2}b^{2}\left(1+{4u^{2} \over a^{4}}+{4v^{2} \over b^{4}}\right)^{3/2}}.}$

Якщо гіперболічний параболоїд

${\displaystyle z={x^{2} \over a^{2}}-{y^{2} \over b^{2}}}$

обертається на кут π/4 в напрямку +z (відповідно до правила правої руки, то результатом є поверхня

${\displaystyle z={1 \over 2}(x^{2}+y^{2})\left({1 \over a^{2}}-{1 \over b^{2}}\right)+xy\left({1 \over a^{2}}+{1 \over b^{2}}\right)}$

і якщо ${\displaystyle \ a=b}$ тоді вираз спрощується до

${\displaystyle z={2 \over a^{2}}xy}$.

Нарешті, прирівнюючи ${\displaystyle a={\sqrt {2}}}$, можна бачити, що гіперболічний параболоїд

${\displaystyle z={x^{2}-y^{2} \over 2}.}$

є конгруентним до поверхні

${\displaystyle \ z=xy}$

що може бути геометричною інтерпретацією (тривимірна номограма) таблиці множення.

Дві параболоїдні ${\displaystyle \mathbb {R} ^{2}\rightarrow \mathbb {R} }$ функції

${\displaystyle z_{1}(x,y)={x^{2}-y^{2} \over 2}}$

і

${\displaystyle \ z_{2}(x,y)=xy}$

є гармонійними кон'югатами, і разом формують аналітичну функцію

${\displaystyle f(z)={1 \over 2}z^{2}=f(x+iy)=z_{1}(x,y)+iz_{2}(x,y)}$

яка є аналітичним продовженням ${\displaystyle \mathbb {R} \rightarrow \mathbb {R} }$ parabolic function ${\displaystyle \ f(x)={1 \over 2}x^{2}.}$

Параболоїди обертання мають властивість фокусувати промені, що проходять паралельно головній оптичній осі, в одній точці, ця властивість використовується при розробці антен та телескопів.

Гіперболічний параболоїд утворюється сіткою прямих, що перетинаються, ця властивість використовується в будівництві. Дах кіноконцертного залу «Україна» в Харкові (1958) був виконан у формі седла. Дах кіноконцертного залу «Ювілейний» в Херсоні (1970) також був виконан у формі седла.

Гіперболоїд інженера Гаріна насправді мав форму параболоїда обертання.

Чайник у формі параболоїда обертання швидше закипає і довше зберігає тепло.

• Параболоїди // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 157. — 594 с.
• Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2024. — 2403 с.(укр.)
• Параболоїди // Термінологічний словник-довідник з будівництва та архітектури / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. — С. 145. — ISBN 978-966-7407-83-4.

• Еліпсоїд
• Гіперболоїд