الگوریتم ارسال-برچسب
الگوریتم ارسال-برچسب (به انگلیسی: push–relabel algorithm) یکی از کارآمدترین الگوریتمها برای محاسبهٔ یک مسئله بیشینه جریان است. الگوریتم عمومی دارای پیچیدگی زمانی است، در حالی که پیادهسازی آن با قانون شیوهٔ رأسها به صورت FIFO دارای زمان اجرای ، با شیوهٔ انتخاب فعالترین رأس دارای پیچیدگی زمانی و با پیادهسازی با کمک دادهساختار درخت پویای ترجان و اسلیتور دارای زمان اجرای است. مجانباً این الگوریتم، از الگوریتم ادموند-کارپ که زمان اجرای آن است کاراتر است.
الگوریتم
[ویرایش]شبکه جریان داده شده که دارای ظرفیت (به انگلیسی: capacity) از گره u تا گره v است که به صورت داده شده، دارای منبع (به انگلیسی: s (source و چاهک (به انگلیسی: t (sink است. میخواهیم بیشترین میزان جریان را که میشود درون شبکه از s به t فرستاد را بیابیم. دو نوع عملیات روی گرهها انجام میشود: push و relabel. بهطور کلی داریم:
- . جریان از u به v. ظرفیت قابل استفاده برابر است با .
- . تنها در صورتی از u به v عمل push را انجام میدهیم که . به ازای همهٔ مقادیر u مقدار یک عدد صحیح غیر منفی است.
- . حاصل جمع جریان وارد شده و خارج شده از u.
بعد از هر گام الگوریتم، جریان یک پیش جریان (به انگلیسی: preflow) است که شرایط زیر را دارد:
- . جریان بین و از ظرفیت بیشتر نباشد.
- . جریان شبکه را در هر دو جهت حفظ میکنیم.
- به ازای تمام گرهها به صورت ،. تنها منبع امکان ایجاد جریان داشته باشد.
توجه داشته باشید که آخرین وضعیت یک پیشجریان از وضعیت متناظر برای یک جریان مجاز در یک در یک شبکه جریان منظم، مجزاست.
ملاحظه میکنیم که طولانیترین مسیر ممکن از s به t دارای بزرگی گره است. بنابراین باید امکان. پذیر باشد که ارتفاع (به انگلیسی: height) را به گرههای هر جریان مجاز اختصاص دهیم، و ، و اگر یک جریان مثبت از u به v وجود داشت، . حال که ما ارتفاع گرهها را تعیین کردیم، جریان در شبکه به حرکت در میآید (مانند جریان آب بر روی پستی و بلندی). بر خلاف الگوریتمهایی مانند فورد-فالکرسون، جریان در طول شبکه، لزماً یک جریان مجاز در اجرای الگوریتم نیست.
بهطور خلاصه، ارتفاعهای گرهها (به جز s و t) تعیین شدهاند، و جریان بین گرهها فرستاده میشود، تا زمانی که تمام جریانهای ممکن به t برسند. سپس میتوانیم افزایش ارتفاع گرههای درونی را ادامه دهیم تا تمام جریانهایی که درون شبکه رفتهاند ولی به t نرسیدهاند، به سمت s بازگردند. یک گره قبل از پایان کار میتواند به ارتفاع برسد، بنا بر این، طولانیترین مسیر ممکن که به s بر میگردد ولی شامل t نیست دارای طول است و . ارتفاع t روی صفر نگه داشته میشود.
Push
[ویرایش]یک push از u به v به معنی فرستادن قسمتی از جریان اضافی ورودی به u به سمت v است. برای رخ دادن یک push باید سه شر�� رعایت شود:
- . جریان ورودی به گره، از جریانی که تاکنون از آن خارج میشده بیشتر باشد.
- . ظرفیت قابل استفاده از u به v.
- . تنها امکان ارسال به گره در ارتفاع کمتر وجود دارد. ما جریانی به اندازهٔ میفرستیم.
Relabel
[ویرایش]یک عمل relabel روی یک گره، افزایش ارتفاع آن است تا جایی که حداقل از یکی از گرههایی که به آن ظرفیت قابل استفاده دارد ارتفاع بیشتری پیدا کند. شرطهایی که برای یک relabel وجود دارد:
- . باید یک حدی برای relabel وجود داشته باشد.
- به ازای هر v برقرار باشد. تنها گرههایی که به آنها ظرفیت قابل استفاده داریم در ارتفاع بیشتری باشند.
هنگام انجام relabel روی u، باید را با کمترین مقدار، مقداردهی کنیم بهطوریکه برای بعضی vها که است، .
الگوریتم push-relabel
[ویرایش]push-relabel در حالت کلی چیدمان زیر را دارد:
- تا زمانی که یک عمل push یا relabel مجاز وجود دارد
- یک push مجاز انجام بده، یا
- یک relabel مجاز
زمان اجرای برای این الگوریتم در حالت کلی برابر است.
تخلیه
[ویرایش]در relabel رو به جلو (به انگلیسی: relabel-to-front)، عمل تخلیه (به انگلیسی: decharge) روی گره u به صورت زیر است:
- تا زمانی که :
- اگر از زمان آخرین relabel همسایهای وجود دارد که بررسی نشده است:
- push کردن جریان به یک همسایهٔ بررسی نشده را انجام بده.
- در غیر این صورت:
- u را relabel کن.
- اگر از زمان آخرین relabel همسایهای وجود دارد که بررسی نشده است:
برای این کار لازم است که برای هر گره، بدانیم از زمان آخرین relabel کردن کدام گرهها بررسی نشدهاند.
الگوریتم relabel رو به جلو
[ویرایش]در الگوریتم relabel رو به جلو، ترتیب push و relabel بدین صورت است:
- تا جای ممکن از s به بیرون جریان بفرست.
- لیستی از تمام رأسها به جز s و t بساز.
- تا زمانی که تمام لیست را پیمایش نکردیم:
- رأس فعلی را تخلیه کن.
- اگر ارتفاع رأس فعلی تغییر کرد:
- رأس فعلی را به جلوی لیست منتقل کن.
- دوباره از جلوی لیست پیمایش کن.
زمان اجرای الگوریتم relabel رو به جلو برابر است. الگوریتم برچسب رو به جلو (به انگلیسی: Relabel To Front Algorithm): الگوریتم ارسال برچسب به ما اجازه میدهد که عملیات اصلی را با هر زمان اجرایی بدست آوریم. به هر حال میتوانیم مسئلهٔ بیشینه شاره را سریع تر از زمان اجرای بدست آوریم. اکنون میخواهیم الگوریتم برچسب رو به جلو که یک الگوریتم ارسال-برچسب با زمان اجرای را بررسی کنیم که به همان خوبی زمان اجرای و بهتر برای شبکههای چگال است. در این الگوریتم فهرستی وجود دارد که شامل همهٔ رأسهای شبکه به جز مبدأ و مقصد است. این الگوریتم فهرست را پیمایش میکند و یک راس را میگیرد و آن را تخلیه میکند و عملیات ارسال بر چسب را تا زمانی که آن راس دیگر افزایش ارتفاع ندارد روی آن انجام میدهد. بهطور مداوم و با تکرار این کار را بر روی رأسهای فهرست انجام میدهد. زمانی که راسی برچسبگذاری شد به جلوی فهرست میرود و الگوریتم کار پیمایش را از اول شروع میکند. به این علت است که این الگوریتم برچسب رو به جلو نام گرفتهاست.
تخلیه
[ویرایش]راس سرشار u با push کردن همهٔ جریانهای اضافی اش در میان یالهای مجاز به رأسهای همسایه تخلیه میشود. راس U اگر لازم باشد برچسبگذاری میشود. کد تخلیهٔ راس سرشار مطابق زیر است:
DISCHARGE(u)
while e[u]> ۰
do v ← current[u]
if v = NIL
then RELABEL(u)
current[u] ← head[N[u]]
elseif cf(u, v)> 0 and h[u] = h[v] + 1
then PUSH(u, v)
else current[u] ← next-neighbor[v]
تحلیل الگوریتم بر چسب رو به جلو
[ویرایش]در این الگوریتم فهرستی وجود دارد که شامل همهٔ رأسهای شبکه به جز s و t (مبدا و مقصد) است. روند پیشروی این الگوریتم نشان میدهد که فهرست همسایههای رأسهای درون فهرست N[u]) l) برای هر راسی درست شدهاست. این همچنین نشان میدهد که [next[u اشاره به راسی دارد که U را در فهرست l دنبال میکند پس مشخص است اگر که راس u آخرین راس در فهرست l باشد next[u]=null. این الگوریتم به این صورت عمل میکند که:
- خط ۱ ارتفاع و جریان اولیه را مقدار دهی میکند.
- خط ۲ فهرست l را با تمام رأسها غیر از راس مبدأ و مقصد مقدار دهی میکند.
- خط ۳ و ۴ آخرین اشاره گر از هر راس u را به اولین راس در فهرست همسایههای u مقدار دهی میکند.
- خط ۵ با اولین راس در فهرست l شروع میکند. هر زمان در داخل حلقه راس u در خط ۸ تخلیه میگردد اگر که u طبق الگوریتم تخلیه برچسبگذاری شده بود در خط ۱۰ به ابتدای فهرست باز میگردد چرا که همانطور که قبلاً گفته شده بود زمانی که برچسبگذاری میشود ارتفاعش افزایش مییابد و اگر ارتفاع افزایش یافته بود آن راس به ابتدای فهرست بر میگردد. این کار زمانی امکانپذیر است که مقدار قبلی ارتفاع راس ذخیره شده باشد.
- خط ۱۱ اشاره گر را به سمت عنصری که x را دنبال میکند میبرد.
RELABEL-TO-FRONT(G, s, t)
1 INITIALIZE-PREFLOW(G, s)
2 L ← V[G] - {s, t}, in any order
3 for each vertex u ∈ V[G] - {s, t}
4 do current[u] ← head[N[u]]
5 u ← head[L]
6 while u ≠ NIL
7 do old-height ← h[u]
8 DISCHARGE(u)
9 if h[u]> old-height
10 then move u to the front of list L
11 u ← next[u]
مثال
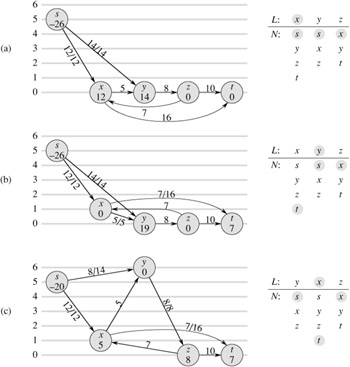
[ویرایش]در شکلهای زیر مثالی برای این الگوریتم آورده شده که توضیح آن آورده شدهاست.
در قسمت a شبکهٔ جریانها قبل از اولین تکرار در حلقه نشان داده شدهاست. ۲۶ مقدار جریان از مبدأ s خارج شده در سمت راست فهرست L که شامل همهٔ رأسها غیر از مبدأ و مقصد است نشان داده شده که در حالت اول راس u را x میگیریم زیر هر راس در فهرست L رأسهای همسایه قرار داده شدهاست. راس x تخلیه میشود به ارتفاع ۱ برچسبگذاری میشود. ۵ واحد از جریان اضافی به y داده میشود. و ۷ مقدار باقیمانده به T وارد میشود. x برچسبگذاری شده پس به سر فهرست باز میگردد. در قسمت b پس از x راس بعدی که تخلیه میشود راس y است شکل عمل تخلیهٔ y را با جرئیات نشان داده. y برچسبگذاری شده پس دوباره به سر فهرست میآید. در قسمت y x , c را در فهرست دنبال میکند. پس راس x دوباره تخلیه میشود x برچسبگذاری نمیشود پس در فهرست باقی میماند و به سر فهرست نمیآید. در قسمت d راس z راس x را دنبال میکند پس تخلیه میشود و به ارتفاع ۱ برچسبگذاری میشود و همهٔ ۸ مقدارش به راس t میرود سپس به ابتدا ی فهرست l میرود چرا که برچسبگذاری شده حال در قسمت e راس y راس z را دنبال میکند پس راس y باید تخلیه شود ولی چون هیچ جریان اضافی ندارد راس x تخلیه میشود و y سر جایش در فهرست باقی میماند. ولی چون x هم جریانی ندارد آن هم در فهرست میماند و این الگوریتم به ته فهرست L میرسد و تمام میشود. هیچ راسی با جریان اضافی نداریم پس جریان بالا بیشینه جریان است. به همین ترتیب توسط الگوریتم بالا بیشینه شاره را با زمان پیدا کردیم.
پیادهسازی نمونه
[ویرایش]پیادهسازی با پایتون:
def relabel_to_front(C, source, sink):
n = len(C) # C is the capacity matrix
F = [[0] * n for _ in xrange(n)]
# residual capacity from u to v is C[u][v] - F[u][v]
height = [0] * n # height of node
excess = [0] * n # flow into node minus flow from node
seen = [0] * n # neighbours seen since last relabel
# node "queue"
list = [i for i in xrange(n) if i != source and i != sink]
def push(u, v):
send = min(excess[u], C[u][v] - F[u][v])
F[u][v] += send
F[v][u] -= send
excess[u] -= send
excess[v] += send
def relabel(u):
# find smallest new height making a push possible,
# if such a push is possible at all
min_height = ∞
for v in xrange(n):
if C[u][v] - F[u][v]> 0:
min_height = min(min_height, height[v])
height[u] = min_height + 1
def discharge(u):
while excess[u]> 0:
if seen[u] <n: # check next neighbour
v = seen[u]
if C[u][v] - F[u][v]> 0 and height[u]> height[v]:
push(u, v)
else:
seen[u] += 1
else: # we have checked all neighbours. must relabel
relabel(u)
seen[u] = 0
height[source] = n # longest path from source to sink is less than n long
excess[source] = Inf # send as much flow as possible to neighbours of source
for v in xrange(n):
push(source, v)
p = 0
while p <len(list):
u = list[p]
old_height = height[u]
discharge(u)
if height[u]> old_height:
list.insert(0, list.pop(p)) # move to front of list
p = 0 # start from front of list
else:
p += 1
return sum(F[source])
توجه داشتهباشید که پیادهسازی بالا چندان کارآمد نیست. این پیادهسازی از الگوریتم ادموند-کارپ حتی برای گرافهای پرتراکم کندتر است.
منابع
[ویرایش]- توماس اچ کورمن, Charles E. Leiserson, رونالد ریوست, and کلیفورد استین. مقدمهای بر الگوریتمها, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 26.4: Push-relabel algorithms, and section 26.5: The relabel-to-front-algorithm.
- Andrew V. Goldberg, رابرت تارجان. A new approach to the maximum flow problem. Annual ACM Symposium on Theory of Computing, Proceedings of the eighteenth annual ACM symposium on Theory of computing, 136–146. 1986
- مشارکتکنندگان ویکیپدیا. «Push-relabel maximum flow algorithm». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۳۰ نوامبر ۲۰۱۱.
پیوند به بیرون
[ویرایش]جستارهای وابسته
[ویرایش]