Delaporte distribution

Delaporte

Probability mass function 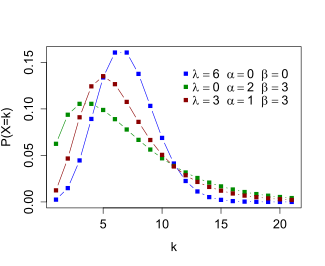When ${\displaystyle \alpha }$ and ${\displaystyle \beta }$ are 0, the distribution is the Poisson. When ${\displaystyle \lambda }$ is 0, the distribution is the negative binomial.
Cumulative distribution function 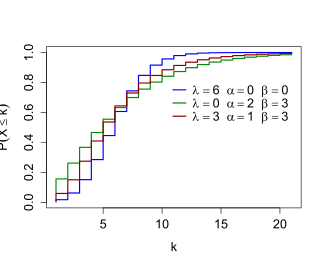When ${\displaystyle \alpha }$ and ${\displaystyle \beta }$ are 0, the distribution is the Poisson. When ${\displaystyle \lambda }$ is 0, the distribution is the negative binomial.
Parameters	${\displaystyle \lambda >0}$ (fixed mean) ${\displaystyle \alpha ,\beta >0}$ (parameters of variable mean)
Support	${\displaystyle k\in \{0,1,2,\ldots \}}$
PMF	${\displaystyle \sum _{i=0}^{k}{\frac {\Gamma (\alpha +i)\beta ^{i}\lambda ^{k-i}e^{-\lambda }}{\Gamma (\alpha )i!(1+\beta )^{\alpha +i}(k-i)!}}}$
CDF	${\displaystyle \sum _{j=0}^{k}\sum _{i=0}^{j}{\frac {\Gamma (\alpha +i)\beta ^{i}\lambda ^{j-i}e^{-\lambda }}{\Gamma (\alpha )i!(1+\beta )^{\alpha +i}(j-i)!}}}$
Mean	${\displaystyle \lambda +\alpha \beta }$
Mode	${\displaystyle {\begin{cases}z,z+1&\{z\in \mathbb {Z} \}:\;z=(\alpha -1)\beta +\lambda \\\lfloor z\rfloor &{\textrm {otherwise}}\end{cases}}}$
Variance	${\displaystyle \lambda +\alpha \beta (1+\beta )}$
Skewness	See #Properties
Excess kurtosis	See #Properties
MGF	${\displaystyle {\frac {e^{\lambda (e^{t}-1)}}{(1-\beta (e^{t}-1))^{\alpha }}}}$

The Delaporte distribution is a discrete probability distribution that has received attention in actuarial science.^[1][2] It can be defined using the convolution of a negative binomial distribution with a Poisson distribution.^[2] Just as the negative binomial distribution can be viewed as a Poisson distribution where the mean parameter is itself a random variable with a gamma distribution, the Delaporte distribution can be viewed as a compound distribution based on a Poisson distribution, where there are two components to the mean parameter: a fixed component, which has the ${\displaystyle \lambda }$ parameter, and a gamma-distributed variable component, which has the ${\displaystyle \alpha }$ and ${\displaystyle \beta }$ parameters.^[3] The distribution is named for Pierre Delaporte, who analyzed it in relation to automobile accident claim counts in 1959,^[4] although it appeared in a different form as early as 1934 in a paper by Rolf von Lüders,^[5] where it was called the Formel II distribution.^[2]

The skewness of the Delaporte distribution is:

${\displaystyle {\frac {\lambda +\alpha \beta (1+3\beta +2\beta ^{2})}{\left(\lambda +\alpha \beta (1+\beta )\right)^{\frac {3}{2}}}}}$

The excess kurtosis of the distribution is:

${\displaystyle {\frac {\lambda +3\lambda ^{2}+\alpha \beta (1+6\lambda +6\lambda \beta +7\beta +12\beta ^{2}+6\beta ^{3}+3\alpha \beta +6\alpha \beta ^{2}+3\alpha \beta ^{3})}{\left(\lambda +\alpha \beta (1+\beta )\right)^{2}}}}$

• Murat, M.; Szynal, D. (1998). "On moments of counting distributions satisfying the k'th-order recursion and their compound distributions". Journal of Mathematical Sciences. 92 (4): 4038–4043. doi:10.1007/BF02432340. S2CID 122625458.