Euklidisches Ei
Zur Navigation springen
Zur Suche springen

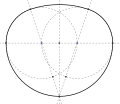
Die beiden Zentren der Kreisbögen und die Nahtstelle liegen auf einer gemeinsamen Geraden g. Die Kreisbögen k und e besitzen in die gemeinsame Tangente t

Ein euklidisches Ei ist ein ausschließlich aus Kreisbögen zusammengesetztes Oval mit genau einer Symmetrieachse. Dabei müssen die Kreisbögen an den Nahtstellen gemeinsame Tangenten besitzen, wodurch die von ihnen gebildete Kurve relativ glatt wirkt.
Aus Sicht der Analysis handelt es sich bei einem euklidisches Ei um eine glatte (ebene) Kurve. Wenn man das euklidische Ei stattdessen abschnittweise anhand (eindimensionaler) Funktionen beschreibt, so liegen diese in der Differentiationsklasse .
Die Existenz einer gemeinsamen Tangente an den Nahtstellen hat zur Folge, dass die Nahtstelle und die beiden Zentren der an ihr aufeinandertreffenden Kreisbögen auf einer gemeinsame Geraden liegen (siehe Zeichnung rechts).
- Beispiele für euklidische Eier
-
Thom-Ei
-
5-Punkte-Ei
-
Goldenes Ei
Literatur
[Bearbeiten | Quelltext bearbeiten]- Robert A. Dixon: Mathographics. Dover, 1991, ISBN 9780486266398, S. 3–12, 76, 159, 161
- Robert A. Dixon: The drawing-out of an egg. In: New scientist, Band 95, Nr. 131, 29. Juli 1982, S. 290–294
- Peter Randall-Page: On the cover: Euclidean Egg III. In Chalkdust, Ausgabe 6, Oktober 2017
- Marija Obradovic, Maja Petrovic: Constructing the Egg Curves using the Golden Ratio of Pentagon. Conference: 2nd International Conference for Geometry and Engineering Graphics “moNGeometrija 2010”, (Proceedings: S. 532–541)
- Angelo Alessandro Mazzotti: A Euclidean Approach to Eggs and Polycentric Curves. In: Nexus Network Journal, Band 16, August 2014, S. 345–387, doi:10.1007/s00004-014-0189-5
- Angelo Alessandro Mazzotti: All Sides to an Oval. Springer, 2017, ISBN 978-3-319-39374-2
Weblinks
[Bearbeiten | Quelltext bearbeiten]Commons: Euklidische Eier – Sammlung von Bildern, Videos und Audiodateien