Transformació geomètrica
Una transformació geomètrica és qualsevol bijecció d'un conjunt que tingui alguna estructura geomètrica cap a si mateix o cap a un altre conjunt d'aquest tipus. Específicament, «Una transformació geomètrica és una funció el domini i el codomini de la qual són conjunts de punts. Molt sovint el domini i el codomini d'una transformació geomètrica són tots dos ℝ² o tots dos ℝ3. Sovint es requereix que les transformacions geomètriques siguin bijectives, és a dir, que tinguin inverses.»[1] L'estudi de la geometria es pot tractar a través de l'estudi d'aquestes transformacions.[2]
Les transformacions geomètriques es poden classificar segons la dimensió dels conjunts en què operen (distingint entre les transformacions del pla i les de l'espai, per exemple). També es poden classificar segons les propietats que preserven:
- les translacions preserven distàncies i angles orientats;
- les isometries preserven distàncies i angles;[3]
- les semblances preserven les raons entre les distàncies;
- les transformacions afins preserven el paral·lelisme;[3]
- les transformacions projectives preserven la col·linealitat,[4]
i cadascuna d'aquestes classes conté la classe anterior.[4]
- Les inversions, d'altra banda, preserven el conjunt de totes les rectes i circumferències en el cas del pla (però poden intercanviar rectes i circumferències).
-
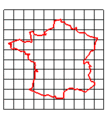
Imatge original
- Els difeomorfismes (transformacions bidiferenciables) són les transformacions que són afins en el primer ordre. Contenen les precedents com a casos especials.[5]
- Les transformacions conformes preserven angles i en el primer ordre són semblances.
- Les transformacions que preserven l'àrea[6] són en el primer ordre transformacions afins de determinant 1.
- Els homeomorfismes (transformacions bicontínues) preserven els entorns dels punts.
Les transformacions del mateix tipus formen grups que poden ser subgrups d'altres famílies de transformacions.
Referències
modifica- ↑ Mathematics for High School Teachers: An Advanced Perspective, p. 84.
- ↑ Venema, Gerard A. Foundations of Geometry (en anglès). Pearson Prentice Hall, 2006, p. 285. ISBN 9780131437005.
- ↑ 3,0 3,1 Geometry Revealed: A Jacob's Ladder to Modern Higher Geometry, p. 131, a Google Books
- ↑ 4,0 4,1 Leland Wilkinson, D. Wills, D. Rope, A. Norton, R. Dubbs – ''The Grammar of Graphics, p. 182, a Google Books
- ↑ stevecheng. «First fundamental form» (PDF). planetmath.org, 13-03-2013. Arxivat de l'original el 2014-07-14. [Consulta: 1r octubre 2014].
- ↑ Bruce E. Meserve. Fundamental Concepts of Geometry, p. 191, a Google Books, p. 191.