Nullpunkt er innen matematikk et begrep som brukes i flere ulike betydninger.
- I et koordinatsystem brukes ordet nullpunkt om begynnelsespunktet, det vil si origo.
- For en funksjon f er et nullpunkt et tall a som gjør at funksjonsverdien f(a) = 0.
For en funksjon i det todimensjonale planet er nullpunktene de punktene der grafen for funksjonen skjærer \(x\)-aksen.
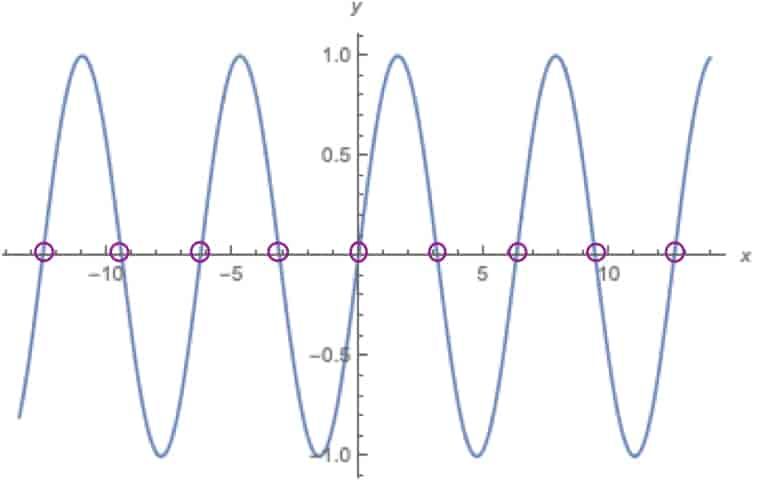
Figur 1 viser polynomet \(y=(x+3)(x+1)(x−1)^2(x−3)\), med nullpunktene markert. Figur 2 viser funksjonen \(y=\sin(x)\), som har nullpunktene \(0,\pm\pi,\pm2\pi,\pm3\pi,\dots\).
Det finnes ingen generell teori for å bestemme nullpunkter for en gitt funksjon. For polynomer finnes det formler for nullpunktene for polynomer opp til og med grad 4. Den norske matematikeren Niels Henrik Abel viste at det er umulig å løse generelle polynomligninger av grad 5 eller høyere ved hjelp av formler.





Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.