MAGENTA
MAGENTA — блочный шифр, разработанный Майклом Якобсоном и Клаусом Хубером для немецкой телекоммуникационной компании Deutsche Telekom AG. MAGENTA является сокращением от Multifunctional Algorithm for General-purpose Encryption and Network Telecommunication Applications (Многофункциональный алгоритм для шифрования в общих целях и телекоммуникационных приложениях).
История
[править | править код]Разработка MAGENTA началась в 1990 году с основными принципами, описанными в неопубликованной книге[1].Основная идея заключалась в применении простой техники, без магических таблиц и постоянных, которая могла быть выполнена как аппаратно, так и программно. Планы заключались в разработке чипа, который мог бы передавать данных со скоростью до 1 Гбит/c и использоваться для шифрования в ATM. К сожалению, аппаратная реализация не появилась на свет, как планировалось, из-за узкого применения, но, несмотря на это, исследования показали, что такой чип возможно разработать[2]. MAGENTA участвовал в конкурсе AES в 1998 году, но выбыл после первого раунда. Шифр стал доступен участникам конференции только в день презентации в отличие от других принимавших участие шифров. MAGENTA использовалась для шифрования данных внутри компании Deutsche Telekom. Следует отметить, что до MAGENTA быстрое преобразование Фурье в криптографических целях использовалось в 2 шифрах. Конкретное название первого не удалось найти[3], он изобретен Жан-Пьером Вассером и зарегистрирован 2 июня 1959 года. Вторым шифром является одна из реализаций алгоритма A3 — Comp-128.
Шифрование
[править | править код]MAGENTA имеет структуру сети Фейстеля. Раундовая функция основана на быстром Адамаровом преобразовании[англ.][4], за исключением того, что вместо сложения и вычитания на каждом этапе к одному из слагаемых применяется S-блок, задаваемый функцией f(x), и затем они складываются по модулю 2.
Пусть множество .Размер блока исходного текста — 128 бит. Размер ключа может принимать 3 значения:
- 128 бит : ,
- 192 бит : ,
- 256 бит : , где .
Пусть F — раундовая функция. Шифр блока M вычисляется таким образом:
- 128 бит — ключ К разбивается на 2 части — К1 и К2. Количество раундов 6. Ключи применяются в таком порядке:
| Раунд | 1 | 2 | 3 | 4 | 5 | 6 |
| Применяемый ключ |
К1 | К1 | К2 | К2 | К1 | К1 |
- 192 бит — ключ К разбивается на 3 части — К1, К2 и К3. Количество раундов 6. Ключи применяются в таком порядке:
| Раунд | 1 | 2 | 3 | 4 | 5 | 6 |
| Применяемый ключ |
К1 | К2 | К3 | К3 | К2 | К1 |
- 256 бит — ключ К разбивается на 4 части — К1, К2, К3 и К4. Количество раундов 8. Ключи применяются в таком порядке:
| Раунд | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Применяемый ключ |
К1 | К2 | К3 | К4 | К4 | К3 | К2 | К1 |
Дешифрование
[править | править код]Следует заметить, что последовательность используемых частей ключа является палиндромом. Пусть . Тогда
Таким образом, дешифрование
Раундовая функция F
[править | править код]Входной блок X размером 128 бит раунда n c раундовым ключом Kn разбивается на 2 части X1 и X2 размером 64 бита каждая.
X = X1X2
После прохождения раунда получаем X' = X2F(X2Kn)
Из зависимости деления на части исходного ключа от количества раундов : длина части ключа, используемая в каждом раунде равна всегда 64 бита.
Следовательно, функция F принимает 128 битовый аргумент и должна возвращать 64-битный или 8-байтовый результат.
Введем вспомогательные функции, через которые затем выразим F:
| Функция | Размер принимаемых(ого) аргументов(а) | Размер возвращаемого значения | Описание |
|---|---|---|---|
| f(x) | 1 байт | 1 байт | Возвращает элемент с номером x в S-блоке |
| A(x, y) | 1 байт | 1 байт | f(x ⊕ f(y)) |
| PE(x, y) | 1 байт | 2 байта | (A(x, y)A(y, x)) — конкатенирует результаты A(x, y) и A(y, x) |
| П(X) | 16 байт | 16 байт | X=X0X1...X14X15 (PE(X0,X8)PE(X1,X9)...PE(X6,X14)PE(X7,X15)) - конкатенирует результаты PE(Xi,Xi+8) i=0...7, Xi имеет размер 1 байт. |
| T(X) | 16 байт | 16 байт | П(П(П(П(X)))) — применяет к X 4 раза функцию П. |
| S(X) | 16 байт | 16 байт | (X0X2X4…X14X1X3X5…X15) — выполняет перестановку байтов X: сначала записываются байты с четным порядковым номером затем с нечетным. |
| С(k, X) | k∈Ν X — 16 байт |
16 байт | Рекурсивная функция: С(1,X) = T(X)) С(k,X) = T(X ⊕ S(C(k-1,X))) |
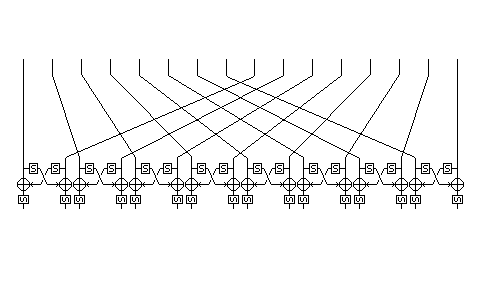
Схема работы функции П(X) :
F полагают равной первым 8 байтам от S(C(n, (X2Kn))), то есть байтам C(n, (X2Kn)) с четным порядковым номером. Изначально n положили равным 7, но тесты показали, что в этом случае шифр возможно взломать. Поэтому затем положили n = 3. Как показали тесты это наилучший выбор, не допускающий криптографических слабостей, сказывающихся на всем шифре. Таким образом,
F полагают равной первым 8 байтам от S(C(3,(X2Kn)))
S-блок
[править | править код]S-блок образуется следующим образом:
Первый элемент — 1, последующие образуются битовым сдвигом влево предыдущего, пока 1 не выйдет за левую границу байта. Соответственно начало блока — 1 2 4 8 16 32 64 128
25610=1 0000 00002, 1 вышла за границу байта. В этом случае нужно сложить по модулю 2 полученное сдвинутое число 0000 00002 c числом 10110=0110 01012:
0000 00002 ⊕ 0110 01012 = 0110 01012 = 10110, то есть после 128 будет стоять 101.
10110=0110 01012 << 1 = 1100 10102=20210, 1 не вышла за границу, следовательно следующий элемент 202.
20210 << 1= 1100 10102 << 1 = 1001 01002, 1 вышла за границу:
1001 01002 ⊕ 0110 01012 = 1111 00012 = 24110.
Последний 256 элемент полагается равным 0. В результате получается такой S-блок:
1 2 4 8 16 32 64 128 101 202 241 135 107 214 201 247 139 115 230 169 55 110 220 221 223 219 211 195 227 163 35 70 140 125 250 145 71 142 121 242 129 103 206 249 151 75 150 73 146 65 130 97 194 225 167 43 86 172 61 122 244 141 127 254 153 87 174 57 114 228 173 63 126 252 157 95 190 25 50 100 200 245 143 123 246 137 119 238 185 23 46 92 184 21 42 84 168 53 106 212 205 255 155 83 166 41 82 164 45 90 180 13 26 52 104 208 197 239 187 19 38 76 152 85 170 49 98 196 237 191 27 54 108 216 213 207 251 147 67 134 105 210 193 231 171 51 102 204 253 159 91 182 9 18 36 72 144 69 138 113 226 161 39 78 156 93 186 17 34 68 136 117 234 177 7 14 28 56 112 224 165 47 94 188 29 58 116 232 181 15 30 60 120 240 133 111 222 217 215 203 243 131 99 198 233 183 11 22 44 88 176 5 10 20 40 80 160 37 74 148 77 154 81 162 33 66 132 109 218 209 199 235 179 3 6 12 24 48 96 192 229 175 59 118 236 189 31 62 124 248 149 79 158 89 178 0
Углубляясь в теорию, можно подытожить: Пусть имеется поле Галуа GF(28) и задающий это поле многочлен — p(x)=x8+x6+x5+x2+1 и пусть α — примитивный элемент поля, p(α)=0. Тогда элемент f(x) в S-блоке с индексом x можно представить как
Свойства используемых функций
[править | править код]f(x)
[править | править код]В течение одного выполнения MAGENTA функция f(x) вычисляется 2304 раза для ключей в 128 и 192 бита и 3072 раза для ключа в 256 бит. Так как функция представляет нелинейную часть алгоритма, она имеет особую важность для анализа всего алгоритма. Следующие свойства f(x) известны:
- f(x) — взаимно-однозначная функция, то есть перестановка над множеством B={0,1}8 — всех восьмибитных двоичных векторов.
- Данная перестановка может быть представлена как результат действия 6 несвязанных циклов длины 198 38 9 5 5 и 1. Согласно комбинаторному анализу, эти значения — «нормальные» и не имеют значительных расхождений с подобными циклами для случайных перестановок. Единственное число остающееся на месте — 161.
- ∀x ∈ B и такого, что f(x) ∈ {1,2,…127} выполнено:
f(x+1) = 2∙f(x), где ∙ — произведение десятичных чисел. ∀(x, y)∈B2 и таких, что f(x)∙f(y)∈{1,2,…255} выполнено: f((x+y) mod 255) = f(x)∙f(y)
- Если рассматривать f(x) как вектор функцию, то есть f(x) = (f7(x), f6(x),…f0(x)), то каждая из 8 булевых функций нелинейна и степени 7. Также всевозможные нетривиальные XOR-комбинации этих функций нелинейны. Явное представление этих функций можно найти здесь.[7] Ещё одно интересное свойство заключается в том, что каждая такая функция имеет 128 слагаемых.
PE(x, y)
[править | править код]Криптоанализ
[править | править код]Оказывается, по крайней мере часть MAGENTA может быть вскрыта методами данного криптоанализа. В качестве разницы между двумя элементами(открытыми текстами или шифрами) берется сложение по модулю 2 между этими элементами. Такое определение разницы обусловлено частым использованием операции xor в данном шифре. Строковые индексы XOR-таблицы представляют собой всевозможные разницы между открытыми текстами, а столбцовые индексы — между шифротекстами. На пересечении конкретного различия открытых текстов, то есть строкового индекса, и конкретного различия шифров, то есть столбцового индекса, стоит число пар открытых текстов, удовлетворяющих данному различию, шифры которых различаются на столбцовый индекс. XOR-таблица для функции f имеет размеры 256*256. Сумма каждой строки и столбца равна 256. Первый элемент первой строки(с индексом 0), отвечающей нулевому различию открытых текстов и шифров, равен 256. Все остальные первой строки элементы равны 0. Аналогично все элементы 1 столбца, кроме первого, равного 256, равны 0. Особенный интерес для дифференциального анализа представляют большие значения — самое большое значение в этой таблицы равно 8. Оно имеет место при таких различиях
| Различие между открытыми текстами |
Различие между шифрами |
|---|---|
| 51 | 35, 66, 154, 155, 250 |
| 102 | 111, 114, 232, 233, 244 |
| 153 | 96, 97, 115, 229, 247 |
| 204 | 18, 19, 38, 207, 251 |
В остальных ячейках таблицы расположены числа 0, 2, 4, 6. Максимальная вероятность перехода для ненулевых различий — .
Для функции PE — также были определены максимальные значения — оно равно 36 для разницы в открытом тексте (234, 234) и нулевой разницы шифров. Максимальная вероятность перехода — ≈ .
Максимальная вероятность перехода для функции T — , для C(3,X) — .
Так как число необходимых пар шифров больше чем величина, обратная вероятности перехода, данный тип дифференциального анализа, основанный на xor-таблицах не применим к MAGENTA. Однако вопрос о других типах остается открытым.
Линейная аппроксимационная таблица для S-блока была вычислена.[8]. Для функций и для каждой xor-суммы , как и для всех линейных функций, было определено, как много цифр значений в таблице согласуется с соответствующими цифрами рассматриваемых линейных функций. В итоге получилось 255 значений между 0 и 256. Нормировка заключалась в вычитании 128. Все значения в таблице лежали на отрезке [-24;26]. Данные значения соответствуют ожидаемым для произвольно выбранных . Значение 26 получается при следующих линейных комбинациях:
Применяя лемму о набегании знаков[англ.] к раундовой функции F(, l=12)
Полученное значение является верхней границей наилучшего аффинного преобразования для F. Приблизительно пар открытый текст — шифр нужно чтобы использовать аффинное линейное приближение с вероятностью [8]. Учитывая предыдущие результаты, для атаки на F необходимо . Следовательно, благодаря нелинейности f(x), MAGENTA не удастся взломать атаками, основанными на линейном криптоанализе.
Примечания
[править | править код]- ↑ K. Huber. Neue Kryptographische Verfahren durch Kombination von Operationen in endlichen Körpern mit der schnellen Walshtransformation. Unpublished manuscript, 1990.
- ↑ K. Huber and S. Wolter. Telekom’s MAGENTA algorithm for en-/decryption in the gigabit/sec range. In ICASSP 1996 Conference Proceedings, volume 6, pages 3233 — 3235, 1996.
- ↑ J.P Vaseur. Verschluesselungsanordnung mit Mischverdrahtung. Deutsches Patentamt Auslegeschrift 1148397, Anmeldetag: 2.Juni 1959, Auslegeschrift: 9.Mai 1963, Anmelder: Compagnie Generale de Telegraphie sans Fil, Paris.
- ↑ S.Y. Kung. VLSI Array Processors. Prentice Hall, 1988.
- ↑ M. Luby and C. Rackoff. How to construct pseudorandom permutations from pseudorandom functions. SIAM J. Computing, 17(2):373-386, April 1988.
- ↑ J. Pieprzyk and B. Sadeghiyan. Design of Hashing Algorithms, volume 756 of Lecture Notes in Computer Science. Springer, 1993.
- ↑ SIT GmbH. Abschlussbericht — Untersuchung eines universellen Kryptoalgorithmus. Technical report, SIT GmbH, 1994.
- ↑ 1 2 E. Biham. On Matsui’s linear cryptanalysis. In Proc. EUROCRYPT '94, volume 658 of Lecture Notes in Computer Science, pages 81-91, 1995.
Ссылки
[править | править код]- M. J. Jacobson, Jr. and K. Hubery The MAGENTA Block Cipher Algorithm
- J. J. G. Savard. The Computer Era. Towards the 128-bit era: AES Candidates. Magenta // A Cryptographic Compendium
- El. Biham, Al. Biryukov, N. Ferguson, L. R. Knudsen, B. Schneier, Ad. Shamir Cryptanalysis of Magenta Архивная копия от 19 августа 2014 на Wayback Machine