Информированный метод поиска
Информи́рованный по́иск (также эвристический поиск, англ. informed search, heuristic search) — стратегия поиска решений в пространстве состояний, в которой используются знания, относящиеся к конкретной задаче. Информированные методы обычно обеспечивают более эффективный поиск по сравнению с неинформированными методами.
Информация о конкретной задаче формулируется в виде эвристической функции. Эвристическая функция на каждом шаге перебора оценивает альтернативы на основании дополнительной информации с целью принятия решения о том, в каком направлении следует продолжать перебор[1].
Эвристические функции
[править | править код]В контексте поиска в пространстве состояний, эвристическая функция (англ. heuristic function) h(n) определена на узлах дерева перебора следующим образом:
- h(n) = оценка стоимости наименее дорогостоящего пути от узла n до целевого узла.
Если n — целевой узел, то h(n) = 0.
Узел для развёртывания выбирается на основе функции оценки (англ. evaluation function)
- f(n) = оценка стоимости наименее дорогостоящего пути решения, проходящего через узел n,
- f(n) = g(n) + h(n),
где функция g(n) определяет стоимость уже пройденного пути от начального узла до узла n.

f1(n) = g(n) + h1(n) — недопустимая эвристика
f2(n) = g(n) + h2(n) — допустимая, но не преемственная
f3(n) = g(n) + h3(n) — преемственная эвристика
Если эвристическая функция h(n) никогда не переоценивает фактическую минимальную стоимость достижения цели (то есть является нижней оценкой фактической стоимости), то такая функция называется допустимой (англ. admissible).
Если эвристическая функция h(n) удовлетворяет условию
- h(a) ≤ cost(a, b) + h(b),
где b — потомок a, то такая функция называется преемственной (англ. consistent).
Если f(n) = g(n) + h(n) — функция оценки, h(n) — преемственная функция, то функция f(n) является монотонно неубывающей вдоль любого исследуемого пути. Поэтому преемственные функции также называются монотонными (англ. monotonic).
Любая преемственная функция является допустимой, но не любая допустимая функция является преемственной.
Если h1(n), h2(n) — допустимые эвристические функции, и для любого узла n верно неравенство h1(n) ≥ h2(n), то h1 является более информированной эвристикой, или доминирует над h2.
Если для задачи существуют допустимые эвристики h1 и h2, то эвристика h(n) = max(h1, h2) является допустимой и доминирует над каждой из исходных эвристик[1][2].
Сравнение эвристических функций
[править | править код]При сравнении допустимых эвристик имеют значение степень информированности и пространственная и временная сложность вычисления каждой из эвристик. Более информированные эвристики позволяют сократить количество развёртываемых узлов, хотя платой за это могут быть затраты времени на вычисление эвристики для каждого узла.
Эффективный коэффициент ветвления (англ. effective branching factor) — среднее число преемников узла в дереве перебора после применения эвристических методов отсечения[1][2]. По эффективному коэффициенту ветвления можно судить о качестве используемой эвристической функции.
Идеальная эвристическая функция (например, таблица поиска) всегда возвращает точные значения длины кратчайшего решения, поэтому дерево перебора содержит только оптимальные решения. Эффективный коэффициент ветвления идеальной эвристической функции близок к 1[1].
Примеры задач поиска
[править | править код]
hm(n)=3+0+0+3+2+4+2+4+1+3+2+2+
+3+3+2=34.
Оптимальное решение состоит из 50 ходов.
В качестве моделей для испытания алгоритмов поиска и эвристических функций часто используются перестановочные головоломки — Пятнашки 3×3[3][4], 4×4[5][6][7], 5×5[8][9][10], 6×6[11], кубик Рубика[9][12], Ханойская башня с четырьмя стержнями[11][13].
В головоломке «Пятнашки» может быть применена эвристика hm, основанная на манхэттенском расстоянии. Более конкретно, для каждой плитки подсчитывается манхэттенское расстояние между её текущим положением и её положением в начальном состоянии; полученные величины суммируются.
Можно показать, что эта эвристика является допустимой и преемственной: за один ход её значение не может измениться более чем на ±1.
Конструирование эвристических функций
[править | править код]Ослабленная задача
[править | править код]Эвристическая функция hm, использующаяся для решения головоломки «Пятнашки», представляет собой нижнюю оценку длины оптимального решения. Помимо этого, hm(n) — это точное значение длины оптимального решения упрощённой версии головоломки, в которой плитки можно передвигать в занятые позиции. В исходной головоломке присутствует ограничение «в одной клетке не должны находиться две и более плитки», которого нет в упрощённой версии. Задача с меньшим количеством ограничений на возможные действия называется ослабленной задачей (англ. relaxed problem); стоимость решения ослабленной задачи является допустимой эвристикой для первоначальной задачи[1], так как любое решение первоначальной задачи является также решением ослабленной задачи.
Подзадача
[править | править код]Допустимая эвристика может быть основана на стоимости решения подзадачи (англ. subproblem) исходной задачи. Любое решение основной задачи одновременно является решением каждой из её подзадач[1].
Подзадачей задачи решения головоломки «Пятнашки» может быть задача перемещения на свои места плиток 1, 2, 3 и 4. Стоимость решения этой подзадачи является допустимой эвристикой для исходной задачи.
Базы данных с шаблонами
[править | править код]
Базы данных с шаблонами[1] (англ. Pattern databases) — вид допустимой эвристики, в основе которого лежит идея хранения точного значения стоимости решения для каждого возможного экземпляра подзадачи[1][6][12].
Пример шаблона для головоломки «Пятнашки» изображён на рисунке справа: в определение подзадачи входят позиции семи фишек, находящихся в первом столбце и в первой строке. Количество конфигураций этого шаблона равно . Для каждой из конфигураций база данных содержит минимальное количество ходов, необходимое для перевода этой конфигурации в целевую конфигурацию подзадачи, показанную на рисунке. Построение базы данных осуществляется методом обратного поиска в ширину[2][6].
Алгоритмы поиска
[править | править код]Поиск по первому наилучшему совпадению
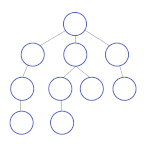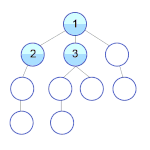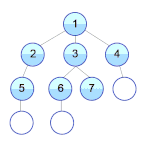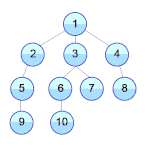
[править | править код]Поиск по первому наилучшему совпадению (англ. best-first search) представляет собой подход, в котором узел для развёртывания выбирается на основе оценочной функции f(n). Для развёртывания выбирается узел с наименьшей оценкой.
Поиск A*
[править | править код]Поиск A* — наиболее известная разновидность поиска по первому наилучшему совпадению. В нём применяется оценка f(n) стоимости наименее дорогостоящего пути решения, проходящего через узел n:
- f(n) = g(n) + h(n), где
- g(n) — стоимость пути от начального узла до узла n,
- h(n) — оценка стоимости пути от узла n до цели.
Если h(n) никогда не переоценивает стоимость достижения цели (то есть является допустимой), то поиск A* является оптимальным.
IDA*
[править | править код]Алгоритм A* с итеративным углублением (iterative deepening A*, IDA*) — применение идеи итеративного углубления в контексте эвристического поиска.
Неинформированный алгоритм итеративного углубления останавливает развёртывание, когда глубина поиска d превышает текущий предел глубины l. Информированный алгоритм IDA* останавливает развёртывание, когда оценка f(n) стоимости пути через текущий узел n превышает текущий предел стоимости пути bound.
Алгоритм IDA* отличается минимальными затратами памяти по сравнению с A* и сравнительно малым (в случае удачного выбора эвристики) количеством развёрнутых узлов по сравнению с IDDFS.
Псевдокод
[править | править код]node текущий узел g стоимость начала решения root..node f оценка стоимости минимального пути через node h(node) эвристическая оценка стоимости остатка пути node..goal cost(node, succ) функция стоимости пути is_goal(node) функция проверки цели successors(node) функция развёртывания узла node procedure ida_star(root, cost(), is_goal(), h()) bound := h(root) loop t := search(root, 0, bound) if t = FOUND then return FOUND if t = ∞ then return NOT_FOUND bound := t end loop end procedure function search(node, g, bound) f := g + h(node) if f > bound then return f if is_goal(node) then return FOUND min := ∞ for succ in successors(node) do t := search(succ, g + cost(node, succ), bound) if t = FOUND then return FOUND if t < min then min := t end for return min end function
MA*
[править | править код]Этот раздел статьи ещё не написан. |
SMA*
[править | править код]SMA* (англ.)
Этот раздел статьи ещё не написан. |
RBFS
[править | править код]Этот раздел статьи ещё не написан. |
См. также
[править | править код]Примечания
[править | править код]- ↑ 1 2 3 4 5 6 7 8 Стюарт Рассел, Питер Норвиг. Составление допустимых эвристических функций // Искусственный интеллект: современный подход = Artificial Intelligence: A Modern Approach. — 2-е изд.. — М.: Вильямс, 2006. — С. 170 — 173. — 1408 с. — ISBN 5-8459-0887-6.
- ↑ 1 2 3 Stefan Edelkamp, Stefan Schrödl. Heuristic search: theory and applications. — Morgan Kaufmann Publishers, 2012. — 712 с. — ISBN 978-0-12-372512-7.
- ↑ Alexander Reinefeld. Complete Solution of the Eight-Puzzle and the Benefit of Node Ordering in IDA*. — 1993.
- ↑ Daniel R. Kunkle. Solving the 8 Puzzle in a Minimum Number of Moves: An Application of the A* Algorithm. — 2001.
- ↑ Richard E. Korf. Depth-first iterative-deepening: An optimal admissible tree search. — 1985.
- ↑ 1 2 3 4 Joseph C. Culberson, Jonathan Schaeffer. Pattern Databases. — 1998.
- ↑ Richard E. Korf, Peter Schultze. Large-Scale Parallel Breadth-First Search. — 2005.
- ↑ Richard E. Korf, Larry A. Taylor. Finding Optimal Solutions to the Twenty-Four Puzzle. — 1996. Архивировано 10 сентября 2015 года.
- ↑ 1 2 Richard E. Korf. Recent Progress in the Design and Analysis of Admissible Heuristic Functions. — 2000.
- ↑ Richard E. Korf, Ariel Felner. Disjoint Pattern Database Heuristics. — 2002. Архивировано 7 мая 2019 года.
- ↑ 1 2 Ariel Felner, Richard E. Korf, Sarit Hanan. Additive Pattern Database Heuristics. — 2004. Архивировано 1 декабря 2021 года.
- ↑ 1 2 Richard E. Korf. Finding Optimal Solutions to Rubik's Cube Using Pattern Databases. — 1997.
- ↑ Richard E. Korf, Ariel Felner. Recent Progress in Heuristic Search: A Case Study of the Four-Peg Towers of Hanoi Problem. — 2007.
- ↑ Основан на Lecture Notes: IDA* Архивная копия от 22 июня 2012 на Wayback Machine
Литература
[править | править код]- Stefan Edelkamp, Stefan Schrödl. Heuristic search: theory and applications. — Morgan Kaufmann Publishers, 2012. — 712 с. — ISBN 978-0-12-372512-7.
- Стюарт Рассел, Питер Норвиг. Составление допустимых эвристических функций // Искусственный интеллект: современный подход = Artificial Intelligence: A Modern Approach. — 2-е изд.. — М.: Вильямс, 2006. — С. 170 — 173. — 1408 с. — ISBN 5-8459-0887-6.