Geometria espacial
Em matemática, geometria espacial é o nome usual para a geometria do espaço tridimensional euclidiano.
A estereometria lida com a medição dos volumes de vários sólidos geométricos ou poliedros (figuras tridimensionais,[1] com latitude, longitude e altitude), incluindo pirâmides, cilindros, cones, troncos de cones, esferas e prismas.[2][3] Um sólido é limitado por um ou mais planos ou superfícies, assim como as superfícies são limitadas por uma ou mais linhas.[1]
Tipos de sólidos
[editar | editar código-fonte]- Regulares - são aqueles limitados por vários de um mesmo tipo de polígono regular e com o mesmo número de polígonos incidindo em cada vértice.[nota 1] Existem apenas cinco sólidos regulares: tetraedro, cubo (hexaedro), octaedro, dodecaedro e icosaedro.[4][1]
Tetraedro regular
Hexaedro regular
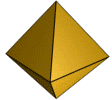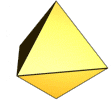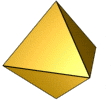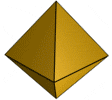Octaedro regular
Dodecaedro regular
Icosaedro regular
- Irregulares - todos os outros, por exemplo, esfera, cilindro, cone,[nota 2] prisma, paralelepípedo, etc.[1]
Cuboctaedro
Notas e referências
Notas
- ↑ O texto de Chambers não especifica esta última restrição; um contra-exemplo é a bipirâmide triangular, formada por seis triângulos equiláteros.
- ↑ O texto de Chambers inclui, erroneamente, o polígono paralelogramo como um sólido irregular.
Referências
- ↑ a b c d Ephraim Chambers, Cyclopaedia, Or an Universal Dictionary of Arts and Sciences (1783), Solid, p.683 [google books]
- ↑ Kiselev 2008.
- ↑ Isidoro de Sevilha, Etimologias, Liber III, 12.1-7 [em linha] (em latim)
- ↑ George Sarton. Ancient Science Through the Golden Age of Greece, pg. 438.