Magnitude
Het hier gebruikte begrip helderheid moet niet verward worden met dat van Helderheid (beeld), uitgedrukt in candela, waarbij de schaal niet logaritmisch is.
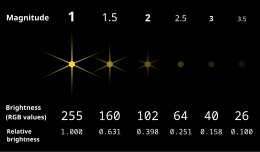
Magnitude (ook wel grootteklasse) is de helderheid van een ster of ander hemellichaam, uitgedrukt op basis van een logaritmische schaal. Magnitude betekent letterlijk grootte of omvang. Hierbij is het volgende te onderscheiden:
- de absolute helderheid wordt bepaald door de eigenschappen van het hemellichaam;
- de schijnbare of waargenomen helderheid hangt af van de absolute helderheid, maar ook van de afstand tot de waarnemer en eventueel verstrooiing, absorptie en zwaartekrachtlenzen.

Hoe groter de helderheid, hoe kleiner het magnitudegetal. Bij kans op verwarring kan men beter zeggen "heeft een kleiner magnitudegetal" dan "heeft een kleinere magnitude".
Golflengte
[bewerken | brontekst bewerken]De magnitude van een hemellichaam wordt gemeten op een bepaalde golflengte, gewoonlijk in het zichtbare of infrarode gebied. De visuele (V) magnitude wordt bepaald bij een golflengte van 551 nm.
Er wordt ook onderscheid gemaakt tussen visuele en fotografische magnitude, sterren hebben verschillende kleuren (zie ook spectraalklasse) en het blote oog heeft zijn maximale gevoeligheid in het geel, terwijl fotografische platen meer gevoelig zijn voor blauw en violet. Een blauwe ster zal in verhouding dus helderder lijken op een fotografische plaat.
Schijnbare magnitude
[bewerken | brontekst bewerken]De schijnbare helderheid van sterren werd door Hipparchus in de oudheid reeds aangegeven met getallen: de helderste sterren kende hij de magnitude of grootte 1 toe en de zwakste de magnitude 6. Een lager magnitudegetal betekent dus een grote helderheid, zoals ook tegenwoordig nog het geval is. In 1856 is deze helderheidsschaal uitgebreid en verfijnd door Norman Pogson, die bepaalde dat een magnitude van 5 minder overeenkomt met een 100 maal zo grote lichtkracht. De magnitude is dus een logaritmische schaal, waarbij een verschil in magnitude van 1 overeenkomt met een helderheidsverhouding van 2,512.
Enkele hemellichamen zijn zo helder dat hun magnitude een negatief getal geeft op de logaritmische schaal. De zon heeft op een onbewolkte dag een magnitude van −26,5, wat men ook noteert als −26m,5 of −26,5 mag, de volle maan heeft op een heldere nacht een magnitude van −12,5. De helderheid van de planeten in het zonnestelsel varieert met hun afstand tot de aarde en hun schijngestalte.
De geïntegreerde magnitude van een hemelobject van enige schijnbare omvang of van een deel van de hemelbol is de totale schijnbare magnitude, dus berekend op basis van al het licht.
Absolute magnitude
[bewerken | brontekst bewerken]De absolute helderheid van een hemellichaam is gedefinieerd als de helderheid die het zou hebben als het op een afstand van 10 parsec zou staan, ongeveer 32,6 lichtjaar. Een absolute helderheid van 5 minder komt weer overeen met een 100 maal zo grote lichtkracht. Als m de schijnbare helderheid van het object is en r de afstand, uitgedrukt in parsec, dan wordt de absolute helderheid gegeven door
- .
Zo heeft de zeer heldere ster Sirius (8,7 lichtjaren) een schijnbare magnitude van −1,46 en een absolute magnitude van (+) 1,43 (op een bijna 4 maal zo grote afstand zou hij bijna 16 maal zo zwak zijn, wat de magnitude bijna 3 hoger zou maken).
Onze zon heeft een absolute magnitude van + 4,88 en tussen andere sterren zou hij onopvallend maar nog wel met het blote oog zichtbaar zijn.
Zonnestelsel
[bewerken | brontekst bewerken]Voor objecten binnen het zonnestelsel, zoals planetoïden is de absolute helderheid gedefinieerd als de helderheid wanneer het object op precies één A.E. van de zon en één A.E. van de Aarde zou staan. De helderheid van objecten die verder van de zon af staan neemt extra snel af omdat er meerdere effecten meespelen:
- als het object verder van de zon staat ontvangt het zelf minder zonlicht en ziet er van gelijke afstand gezien al donkerder uit;
- een object dat verder van ons af staat lijkt kleiner en heeft dus een kleiner lichtgevend oppervlak (dit in tegenstelling tot sterren die vrijwel altijd zo ver weg staan dat ze een puntbron zijn);
- de schijnbare lichtsterkte neemt af met het kwadraat van de afstand, althans bij gelijke oppervlakte en oppervlaktehelderheid.
Nulpunt
[bewerken | brontekst bewerken]De magnitudeschaal is in het verleden zo gedefinieerd dat de A0V ster Wega een schijnbare magnitude 0 heeft. Dit geldt voor elke golflengteband. In de praktijk is Wega een veranderlijke ster en tegenwoordig zijn er nauwkeurigere bepalingen mogelijk.
Voor de absolute bolometrische magnitude, gebaseerd op de bolometrische lichtkracht, is het nulpunt gedefinieerd als corresponderend met een totale bolometrische lichtkracht van 3,0128 × 1028 W.[1] De Zon met een lichtkracht van 3,828 × 1026 W heeft daarmee een absolute magnitude van 4,74, en een relatieve magnitude van −26,83.
Zichtbaarheid
[bewerken | brontekst bewerken]Afhankelijk van de omstandigheden kunnen sterren tot een bepaalde magnitude met het blote oog gezien worden. In een stad met veel lichtvervuiling zullen misschien sterren tot een grensmagnitude 2 gezien kunnen worden, op een hoge bergtop ver van alle omgevingslicht is de grensmagnitude ongeveer 6. Dit is geen absolute grens, het hangt ook van de waarnemer zelf af en zelfs van de manier van kijken. De gele vlek in het centrum van het gezichtsveld is minder gevoelig voor licht dan de gebieden met staafjes er naast, maximale gevoeligheid wordt bereikt door net "naast" het object te kijken. Dit wordt ook wel perifeer waarnemen genoemd.
Zichtbaarheid hangt af van de hoeveelheid invallend licht in oog of telescoop. Een oogpupil heeft in het donker een diameter van ongeveer 6 mm, maar zelfs een (relatief kleine) telescoop heeft al een tien keer zo grote diameter. De oppervlakte en de hoeveelheid invallend licht zijn dan honderd keer zo groot, wat een winst van 5 magnitudes oplevert. De grensmagnitude zal hier dus 11 zijn. Grotere telescopen leveren meer winst op, voor iedere factor 10 in diameter dus 5 magnitudes. Bij fotografische waarneming kan de grensmagnitude nog verder verlegd worden door langer te belichten. Het licht wordt hier als het ware over een langere tijd opgespaard.
In de overzichten van de sterren wordt altijd de schijnbare visuele magnitude aangegeven, tenzij anders vermeld. De lijst van helderste sterren gaat tot magnitude 2.
De geïntegreerde magnitude van een hemelobject is niet noodzakelijk een goede maat voor de zichtbaarheid, omdat licht geconcentreerd in een punt beter zichtbaar is dan als dit licht over een (niet zeer kleine) ruimtehoek is uitgesmeerd.[2] Bij een niet-puntbron is er daarom aanvullend het begrip oppervlaktehelderheid, op basis van de lichtkracht per eenheidsruimtehoek. Omdat een steradiaal erg groot is kan als eenheidsruimtehoek bijvoorbeeld ook een vierkante boogseconde genomen worden. Voor bijvoorbeeld de Zon is de schijnbare diameter 9,30 mrad of 1920 arcsec, en de ruimtehoek 67,9 μsr of 2,89 karcsec². De 1361 W/m² (zonneconstante) is dus 20,0 MW/m²/sr of 471 μW/m²/arcsec². Per sr is de relatieve magnitude −37,25, en per arcsec² is deze −10,68. Voor de volle maan zijn deze waarden ongeveer 14,5 hoger, dus respectievelijk ongeveer −23 en 4.
Voorbeelden
[bewerken | brontekst bewerken]Deze tabel geeft een idee van enkele schijnbare magnitudes met elkaar vergeleken.
| Schijnbare helderheid (V) | Hemellichaam |
|---|---|
| –30,30 | Sirius vanaf 1 AU |
| –26,74 | De Zon vanaf Aarde (400.000x de volle maan) |
| –18,20 | De Zon vanaf Pluto in haar aphelion |
| –12,92 | Maximum helderheid van de Volle maan |
| –11,20 | De Zon vanaf Sedna in haar aphelion |
| –7,50 | De SN 1006 supernova van 1006 na Chr., de helderste astronomische gebeurtenis in geschreven geschiedenis |
| –6,00 | De Krab supernova (SN 1054) of 1054 na Chr. (6500 lichtjaar van hier) |
| –4,89 | Maximum helderheid van Venus, half belicht |
| –4,00 | Zwakste objecten overdag wanneer zon volop schijnt met het blote oog waarneembaar |
| –2,50 | Minimum helderheid van de nieuwe maan |
| –1,47 | helderste ster (buiten de zon) aan de hemel: Sirius |
| –0,72 | op een na helderste ster: Canopus |
| –0,04 | op vier na helderste ster Arcturus |
| +0,03 | Vega, die het originele basispunt van de helderheidsschaal is |
| +0,50 | De Zon gezien vanaf Alpha Centauri |
| +3,03 | De SN 1987A supernova in de Grote Magelhaense Wolk 168.000 lichtjaar van hier |
| +3 tot +4 | Zwakste sterren zichtbaar in een stedelijke wijk met blote oog |
| +3,44 | het wel bekende Andromedastelsel (M31) |
| +5,72 | Het Triangulumstelsel |
| +6,50 | limiet van het menselijk blote oog |
| +6,90 | M81 |
| +7 tot +8 | Extreme limiet van het blote oog bij klasse 1 Bortle Dark-Sky Scale, de donkerste hemelen op aarde |
| +9,50 | Zwakste objecten zichtbaar met behulp van een 7x50 verrekijker onder normale omstandigheden |
| +12,91 | Helderste quasar: 3C 273 |
| +16,80 | 136472 Makemake |
| +22,00 | limiet van de Ritchey-Chrétien telescope |
| +27,00 | Zwakste objecten waarneembaar in zichtbaar licht met 8m telescopen op de grond |
| +31,50 | limiet van de Hubble Space Telescope |
| +39,00 | zwakste objecten detecteerbaar met de huidige technologie |
Zie ook
[bewerken | brontekst bewerken]- ↑ (en)
 RESOLUTION B1 - The IAU Strategic Plan 2010-2020: Astronomy for Development. Gearchiveerd op 6 maart 2023. Geraadpleegd op 31 juli 2023.
RESOLUTION B1 - The IAU Strategic Plan 2010-2020: Astronomy for Development. Gearchiveerd op 6 maart 2023. Geraadpleegd op 31 juli 2023.
- ↑ Gearchiveerde kopie. Gearchiveerd op 29 september 2017. Geraadpleegd op 29 september 2017.

