Binaire mathematische morfologie
Binaire mathematische morfologie is het specifiek toepassen van morfologische bewerkingen op binaire beelden. Praktisch worden deze operaties veel uitgevoerd en is het een ideale manier om het concept van een operatie weer te geven. Met de vier basisoperatoren kunnen verschillende bewerkingen worden uitgevoerd. Deze operatoren zijn: dilatatie, erosie, sluiting en opening. Bij een binair beeld kan iedere pixel een waarde hebben van 1 of 0. Een binair beeld wordt beschouwd als een verzameling. Een pixel die deel uitmaakt van de verzameling, heeft een waarde 1 en een pixel dat geen deel uitmaakt van de verzameling heeft een waarde 0.
In binaire mathematische morfologie wordt een afbeelding gezien als een deelverzameling van een euclidische ruimte van een bepaalde dimensie .
Definities
[bewerken | brontekst bewerken]Om een mathematische morfologie toe te passen zijn drie elementen nodig, het invoerbeeld, de operator en het structuurelement.
Een invoerbeeld kan ieder binair beeld zijn.
De meest voorkomende operatoren zijn:
- Dilatatie
- Erosie
- Sluiting
- Opening
- Hit-or-miss
Het laatste element is een structuurelement. Dit is een verzameling die meestal kleiner is dan het invoerbeeld, en uit slechts enkele pixels bestaat. De vorm en de positie van de oorsprong bepalen hoe het structuurelement zal inwerken op het binaire invoerbeeld.
Primaire operatoren
[bewerken | brontekst bewerken]De verschillende operatoren kunnen worden opgedeeld in verschillende groepen. De primaire operatoren zijn twee operatoren die aan de basis liggen van binaire mathematische morfologie. Via deze primaire operatoren kunnen alle bewerkingen worden uitgevoerd op een binair beeld. Iedere bewerking kan worden herleid tot een reeks van primaire operatoren.
Dilatatie
[bewerken | brontekst bewerken]
Een dilatatie heeft als effect dat objecten dikker worden, kleine gaten worden opgevuld en randen worden afgerond. Als het invoerbeeld is en het structuurelement, kan de dilatatie worden gegeven als:
Een dilatatie wordt vaak gebruikt om gaten in een beeld op te vullen. Een bekend probleem is dat alles "dikker" wordt in de afbeelding, wat nadelige resultaten oplevert.
Erosie
[bewerken | brontekst bewerken]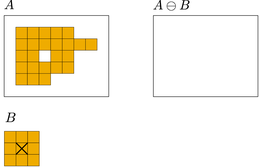
Een erosie is het tegenovergestelde van een dilatatie. Door een erosie zal het object krimpen en worden dunne lijnen en geïsoleerde pixels verwijderd. Als het invoer beeld is en het structuurelement, kan de erosie worden gegeven als:
Secundaire operatoren
[bewerken | brontekst bewerken]Secundaire operatoren bestaan uit het achtereenvolgens toepassen van een erosie of een dilatatie met hetzelfde structuurelement. De volgorde waarin de erosie en de dilatatie worden toegepast is zeer belangrijk. De meest voorkomende secundaire operatoren zijn de sluiting en de opening.
Sluiting
[bewerken | brontekst bewerken]Een sluiting wordt gevormd door een dilatatie gevolgd door een erosie met hetzelfde structuurelement. Het effect van een sluiting is dat de nadelige effecten van een dilatatie gedeeltelijk teniet worden gedaan. Als het invoerbeeld is en het structuurelement, kan de sluiting worden gegeven als:
Opening
[bewerken | brontekst bewerken]Een opening wordt gevormd door een erosie gevolgd door een dilatatie. Het effect van een opening is dat de nadelige effecten van een erosie gedeeltelijk teniet worden gedaan. Als het invoerbeeld is en het structuurelement, kan de opening worden gegeven als:
Eigenschappen van operatoren
[bewerken | brontekst bewerken]Twee belangrijke bewerkingen zijn:
- Het complement van een beeld is:
- De reflectie van een beeld is:
Referenties
[bewerken | brontekst bewerken]Digital Image Processing by Rafael C. Gonzalez and Richard E. Woods, ISBN 0-13-505267-X















