Projektív geometria
| Matematika |
|---|
| A matematika alapjai |
| Algebra |
| Analízis |
| Geometria |
| Számelmélet |
| Diszkrét matematika |
| Alkalmazott matematika |
| Általános |
A projektív geometria a következőket jelentheti:
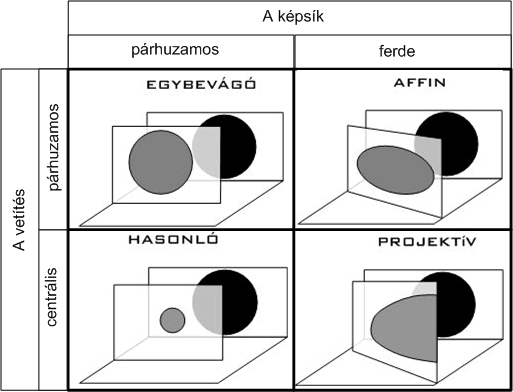
1. A matematikának, azon belül a geometriának az a területe, ami az alakzatoknak a centrális vetítés közben változatlan jellemzőivel foglalkozik.
2. A nemeuklideszi geometriai rendszerek egyike, ami az euklideszi párhuzamosságot a síkban „minden egyenespár metsző” axiómával helyettesíti.
A két értelmezés hagyományosan két különböző tárgyalásmódot, de formális szempontból azonos tárgykört és tételeket jelent.
Története
[szerkesztés]A projektív geometria a matematikának olyan fejezete, amelynek kidolgozásához a képzőművészettől kapta az indítást, de mérnöki, főleg építészeti igény is inspirálta.
A képalkotás geometriai alapjaival már Eukleidész is foglalkozott Optika c. művében. Néhány projektív geometriai tétel (Papposz-tétel) már az ókorban is ismeretes volt, s jó néhányat bizonyítottak be a 17. századtól kezdve (Gérard Desargues, Blaise Pascal).
A térábrázolást a gyakorlatban is művelő festők-építészek tollából igen sok tanulmány és amolyan receptúra jelent meg. Különösen felgyorsult ez a tevékenység az olasz reneszánszban. Filippo Brunelleschi (Firenze, 1377–1446), a reneszánsz első nagy építésze, a perspektíva matematikai, geometriai elméletét kezdte vizsgálni. Az elméletnek tanítványa Leon Battista Alberti (1404–1472) adta a végleges formát (1442), majd az elmélet és az alkalmazás fejlesztéséhez a korszak szinte minden nevezetes művésze hozzájárult: Piero della Francesca (1420?–1492); Jean Pèlerin (1445?–1524). Különösen Leonardo da Vinci (1452–1519) és Albrecht Dürer (1471–1528) munkája volt jelentős.
A téma rendszeres matematikai tanulmányozása a 18. század végén kezdődött. Jean-Victor Poncelet (1788–1867) – a Napóleon oroszországi hadjárata során fogságba esett francia tiszt, az École Politechnique egykori hallgatója, Gaspard Monge tanítványa – 1813-ban írta, 1822-ben publikálta a projektív geometriát megalapozó munkáját: Traité des propiétés projectives des figures (Értekezés az alakzatok projektív tulajdonságairól). A kérdéskör kifejtésében részt vevő további nevek: Jacob Steiner (1796–1863); Karl Georg Christian von Staudt (1798–1867); Michel Chasles (1793–1880).
A perspektíva geometriája mellett a műszaki ábrázolás igényeit kielégítő „egyszerű” ábrázoló geometria a Monge-féle kétképsíkos ábrázolással az ipari szervezettség szintjére emelkedett.
Ideális térelemek
[szerkesztés]
Nem sokkal a perspektíva törvényeinek felfedezése után született meg az ideális pont fogalma. Nem is egy, hanem két forrást is ismerünk. Az egyik a csillagász Johannes Kepler (1571–1630), aki a parabola másik fókuszáról mondja, hogy végtelen távolságban van (szemben az ellipszis és a hiperbola végesben fekvő fókuszaival). A másik a francia építész Gérard Desargues (1591–1661), aki a párhuzamosok végtelen távoli közös végéről ír.
Az euklideszi térelemeket az ideális térelemekkel (pontok, egyenesek, sík) kiegészítve olyan szerkezetű tér absztrakt modelljét kapjuk, amelyben az euklideszi- és a Bolyai–Lobacsevszkij-féle párhuzamossági axiómák egyike sem teljesül. A projektív síkban két egyenes mindig metsző, az euklideszi párhuzamosok közös pontja ideális pont. A projektív térben két sík közönséges vagy ideális egyenesben metszik egymást.
Az ábrázolás és a vele kapcsolatos problémák végső szintézise 1872-ben született meg. Ekkor hangzott el Felix Klein (1849–1925) német matematikus nevezetes előadása, amelyre a matematika története az erlangeni program néven utal. Klein hívta fel a figyelmet arra, hogy a geometriai transzformációkat osztályozhatjuk aszerint, hogy egyes alakzatoknak milyen tulajdonságait örökítik, melyik tulajdonság invariáns a transzformáció során. E rendszerezés szerint a projektív transzformációk osztályát az jellemzi, hogy a folytonosság, az illeszkedés invarianciáján kívül az egyenesek képe egyenes és a pontsorok, sugársorok négyeseinek kettősviszonya megmarad. A projekció tehát a szabad leképezés és a merev egybevágóság között helyezkedik el.
További információk
[szerkesztés]Források
[szerkesztés]- Kárteszi Ferenc: Ábrázoló geometria (Tankönyvkiadó, 1957)
- Hajós György: Bevezetés a geometriába (Tankönyvkiadó, 1960, 1971) ISBN 963 18 31736
- Gulyás Dénes: A térábrázolás (A képzőművészet iskolája) (Képzőművészeti Alap, 1977)
- Coxeter, H.S.M.: Projektív geometria (Gondolat, 1986)
- Hack Frigyes: A 3D-grafika geometriai alapjai (ELTE, 2002)

