« Quadrangle complet » : différence entre les versions
m wikification |
nom |
||
| Ligne 1 : | Ligne 1 : | ||
{{Voir homonymes|Quadrangle (homonymie)}} |
{{Voir homonymes|Quadrangle (homonymie)}} |
||
En [[géométrie plane]], un '''quadrangle complet''' est la figure formée par quatre points A, B, C et D, tels que trois quelconques d'entre eux ne soient pas alignés : ce sont les ''sommets'' du quadrangle. Les six droites joignant ces points deux à deux sont les ''côtés'' du quadrangle<ref name=Didier>{{ouvrage |
En [[géométrie plane]], un '''quadrangle complet''' est la figure formée par quatre points A, B, C et D, tels que trois quelconques d'entre eux ne soient pas alignés : ce sont les ''sommets'' du quadrangle. Les six droites joignant ces points deux à deux sont les ''côtés'' du quadrangle<ref name=Didier>{{ouvrage |
||
| prénom1 = W |nom1 = Gellert |
| prénom1 = W |nom1 = Gellert |
||
| prénom2 = H. | nom2 = Küstner |
| prénom2 = H. | nom2 = Küstner |
||
Version du 7 février 2020 à 12:10
En géométrie plane, un quadrangle complet ou quadrangle est la figure formée par quatre points A, B, C et D, tels que trois quelconques d'entre eux ne soient pas alignés : ce sont les sommets du quadrangle. Les six droites joignant ces points deux à deux sont les côtés du quadrangle[1].
Deux côtés qui n'ont pas de sommet en commun sont dits opposés. Deux côtés opposés (non parallèles) ont un point commun appelé point diagonal du quadrangle. Un quadrangle complet (dont les côtés ne sont pas parallèles) a quatre sommets, six côtés et trois points diagonaux.
Le quadrangle est à distinguer de son dual projectif, le quadrilatère complet qui est formé de quatre droites, sans triplet de droites concourantes, et de leur six points d'intersection et contient trois diagonales[1] et trois points diagonaux.
Quadrangle inscriptible
Un quadrangle est dit inscriptible si ses quatre sommets sont sur un même cercle.

Pour qu'un quadrangle soit inscriptible, il faut et il suffit que deux couples de côtés opposés soient antiparallèles. Le troisième couple est alors antiparallèle à chacun des deux autres.
Soit ABCD un quadrangle dont les côtés opposés (AB) et (CD) se coupent en I :
ABCD est inscriptible si et seulement si IA × IB = IC × ID.
IA × IB est la puissance du point I par rapport au cercle circonscrit au quadrangle.
Les angles et sont égaux. Les triangles IAD et ICB sont (inversement) semblables (les angles inscrits et sont supplémentaires - dans la figure ci-dessus - ou égaux).
Quadrangle orthocentrique
Un quadrangle est dit orthocentrique quand n'importe quel des quatre points est l'orthocentre du triangle formé par les trois autres points[2].
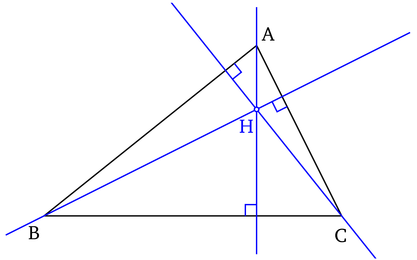
Les trois sommets du triangle et leur orthocentre forment un quadrangle orthocentrique : chacun de ces points est l'orthocentre du triangle formé par les trois autres points.

Dans un triangle, le centre du cercle inscrit dans le triangle et les centres des cercles exinscrits forment également un quadrangle orthocentrique.
Notes et références
- W Gellert, H. Küstner, M. Hellwich et H. Kästner, Petite encyclopédie des mathématiques, Didier, , p. 603
- «Quadrangle orthocentrique» dans le Glossaire de Publimath




