Tide

The tide is the cyclic rising and falling of Earth's ocean surface caused by the tidal forces of the Moon and the Sun acting on the Earth. Tides cause changes in the depth of the sea, and also produce oscillating currents known as tidal streams, making prediction of tides important for coastal navigation (see Tides and navigation, below). The strip of seashore that is submerged at high tide and exposed at low tide, the intertidal zone, is an important ecological product of ocean tides.

The changing tide produced at a given location on the Earth is the result of the changing positions of the Moon and Sun relative to the Earth coupled with the effects of the rotation of the Earth and the local bathymetry (the underwater equivalent to topography). Though the gravitational force exerted by the Sun on the Earth is almost 200 times stronger than that exerted by the Moon, the tidal force produced by the Moon is about twice as strong as that produced by the Sun. The reason for this is that the tidal force is related not to the strength of a gravitational field, but to its gradient. The field gradient decreases with distance from the source more rapidly than does the field strength; as the Sun is about 400 times further from the Earth than is the Moon, the gradient of the Sun's field, and thus the tidal force produced by the Sun, is weaker.

The maximum water level is called "high tide" or "high water" and the minimum level is "low tide" or "low water." If the ocean were a constant depth, and there were no land, high water would occur as two bulges in the height of the oceans--one bulge facing the Moon and the other on the opposite side of the earth, facing away from the Moon. There would also be smaller, superimposed bulges on the sides facing toward and away from the Sun. For an explanation see below under Tidal physics. At any given point in the ocean, there are normally two high tides and two low tides each day just as there would be for an earth with no land; however, rather than two large bulges propagating around the earth, with land masses in the way the result is many smaller bulges propagating around amphidromic points, so there is no simple, general rule for predicting the time of high tide from the position of the Moon in the sky. The common names of the two high tides are the "high high" tide and the "low high" tide; the difference in height between the two is known as the "daily inequality." The daily inequality is generally small when the moon is over the equator. The two low tides are called the "high low" tide and the "low low" tide. On average, high tides occur 12 hours 24 minutes apart. The 12 hours is due to the Earth's rotation, and the 24 minutes to the Moon's orbit. This is the "principal lunar semi-diurnal" period, abbreviated as the M2 tidal component, and it is, on average, half the time separating one lunar zenith from the next. The M2 component is usually the biggest one, but there are many others as well due to such complications as the tilt of the earth's axis and the inclination of the lunar orbit. The lunar cycle is what is tracked by tide clocks.

The time between high tide and low tide, when the water level is falling, is called the "ebb." The time between low tide and high tide when the tide is rising, is called "flow," or "flood." At the times of high tide and low tide, the tide is said to be "turning," also slack tide.

The height of the high and low tides (relative to mean sea level) also varies. Around new and full Moon when the Sun, Moon and Earth form a line (a condition known as syzygy), the tidal forces due to the Sun reinforce those of the Moon. The tides' range is then at its maximum: this is called the "spring tide," or just "springs" and is derived not from the season of spring but rather from the verb "to jump" or "to leap up." When the Moon is at first quarter or third quarter, the Sun and Moon are at 90° to each other and the forces due to the Sun partially cancel out those of the Moon. At these points in the Lunar cycle, the tide's range is at its minimum: this is called the "neap tide," or "neaps".

Spring tides result in high waters that are higher than average, low waters that are lower than average, slack water time that is shorter than average and stronger tidal currents than average. Neaps result in less extreme tidal conditions. Normally there is a seven day interval between springs and neaps.

The relative distance of the Moon from the Earth also affects tide heights: When the Moon is at perigee the range increases, and when it is at apogee the range is reduced. Every 7½ lunations, perigee and (alternately) either a new or full Moon coincide; at these times the range of tide heights is greatest of all, and if a storm happens to be moving onshore at this time, the consequences (in the form of property damage, etc.) can be especially severe. (Surfers are aware of this, and will often intentionally go out to sea during these times, as the waves are larger at these times.) The effect is enhanced even further if the line-up of the Sun, Earth and Moon is so exact that a solar or lunar eclipse occurs concomitant with perigee.

In most places there is a delay between the phases of the Moon and its effect on the tide. Springs and neaps in the North Sea, for example, are two days behind the new/full Moon and first/third quarter, respectively. The reason for this is that the tide originates in the southern oceans, the only place on the globe where a circumventing wave (as caused by the tidal force of the Moon) can travel unimpeded by land.

Many people also believe the time difference between high tides and low tides to be the same. Times between high and low tides will always differ (many people believe them to be 6 hours and 12 minutes, from which they may deviate).

The resulting effect on the amplitude, or height, of the tide travels across the oceans. It is known that it travels as a single broad wave pulse northwards over the Atlantic. This causes relatively low tidal ranges in some locations (nodes) and high ones in other places. This is not to be confused with tidal ranges caused by local geography, as can be found in Nova Scotia, the Bristol Channel, the Channel Islands, and the English Channel. In these places tidal ranges can be over 10 metres.

The Atlantic tidal wave arrives after approximately a day in the English Channel area of the European coast and needs another day to go around the British Isles in order to have an effect in the North Sea. Peaks and lows of the Channel wave and North Sea wave meet in the Strait of Dover at about the same time but generally favour a current in the direction of the North Sea.

The exact time and height of the tide at a particular coastal point is also greatly influenced by the local topography. There are some extreme cases: the Bay of Fundy, on the east coast of Canada, features the largest well-documented tidal ranges in the world, 16 metres (53 ft), because of the shape of the bay. Southampton in the United Kingdom has a double high tide caused by the flow of water around the Isle of Wight, and Weymouth, Dorset has a double low tide because of the Isle of Portland. Ungava Bay in Northern Quebec, north eastern Canada, is believed by some experts to have higher tidal ranges than the Bay of Fundy (about 17 metres or 56 ft), but it is free of pack ice for only about four months every year, whereas the Bay of Fundy rarely freezes even in the winter.

There are only very slight tides in the Mediterranean Sea and the Baltic Sea due to their narrow connections with the Atlantic Ocean. Extremely small tides also occur for the same reason in the Gulf of Mexico and Sea of Japan. On the southern coast of Australia, because the coast is extremely straight (partly due to the tiny quantities of runoff flowing from rivers), tidal ranges are equally small.

Ignoring external forces, the ocean's surface defines a geopotential surface or geoid, where the gravitational force is directly towards the centre of the Earth and there is no net lateral force and hence no flow of water.

Now consider the effect of added external, massive bodies such as the Moon and Sun. These massive bodies have strong gravitational fields that diminish with distance in space. It is the spatial differences, called the gradient in these fields that deform the geoid shape. This deformation has a fixed orientation relative to the influencing body and the rotation of the Earth relative to this shape drives the tides around. Gravitational forces follow the inverse-square law (force is inversely proportional to the square of the distance), but tidal forces are inversely proportional to the cube of the distance. The Sun's gravitational pull on Earth is on average 179 times bigger than the Moon's, but because of its much greater distance, the Sun's field gradient and thus its tidal effect is smaller than the Moon's (about 46% as strong). For simplicity, the next few sections use the word "Moon" where also "Sun" can be understood.

Since the Earth's crust is solid, it moves with everything inside as one whole, as defined by the average force on it. For a geoid shape this average force is equal to the force on its centre. The water at the surface is free to move following forces on its particles. It is the difference between the forces at the Earth's centre and surface which determine the effective tidal force.

At the point right "under" the Moon (the sub-lunar point), the water is closer than the solid Earth; so it is pulled more and rises. On the opposite side of the Earth, facing away from the Moon (the antipodal point), the water is farther from the moon than the solid earth, so it is pulled less and effectively moves away from Earth (i.e. the Earth moves more toward the Moon than the water does), rising as well. On the lateral sides, the water is pulled in a slightly different direction than at the centre. The vectorial difference with the force at the centre points almost straight inwards to Earth. It can be shown that the forces at the sub-lunar and antipodal points are approximately equal and that the inward forces at the sides are about half that size. Somewhere in between (at 55° from the orbital plane) there is a point where the tidal force is parallel to the Earth's surface. Those parallel components actually contribute most to the formation of tides, since the water particles are free to follow. The actual force on a particle is only about a ten millionth of the force caused by the Earth's gravity.

These minute forces all work together:

• pull up under and away from the Moon
• pull down at the sides
• pull towards the sub-lunar and antipodal points at intermediate points

So in an ocean of constant depth on an Earth with no land, two bulges would form pointing towards the Moon just under it and away from it on Earth's far side. In reality, the presence of land masses and the depth profile of oceans distort this simple pattern significantly.

Since the Earth rotates relative to the Moon in one lunar day (24 hours, 48 minutes), each of the two bulges travels around at that speed, leading to one high tide every 12 hours and 24 minutes. The theoretical amplitude of oceanic tides due to the Moon is about 54 cm at the highest point. This is the amplitude that would be reached if the ocean were uniform with no landmasses and Earth not rotating.

The Sun similarly causes tides, of which the theoretical amplitude is about 25 cm (46% of that of the Moon) and the cycle time is 12 hours.

At spring tide the two effects add to each other to a theoretical level of 79 cm, while at neap tide the theoretical level is reduced to 79cm quared.

Real amplitudes differ considerably, not only because of global topography as explained above, but also because the natural period of the oceans is in the same order of magnitude as the rotation period: about 30 hours. If there were no land masses and the ocean bottom were flat, it would take about 30 hours for a long wavelength ocean surface wave to propagate halfway around the Earth (by comparison, the natural period of the Earth's crust is about 57 minutes). This means that, if the Moon suddenly vanished, and there were no land, the level of the oceans would oscillate with a period of 30 hours with a slowly decreasing amplitude while dissipating the stored energy. This 30 hour value is a simple function of terrestrial gravity, the average depth of the oceans, and the circumference of the Earth.

The distances of Earth from the Moon or the Sun vary, because the orbits are not circular, but elliptical. This causes a variation in the tidal force and theoretical amplitude of about ±18% for the Moon and ±5% for the Sun. So if both are in closest position and aligned, the theoretical amplitude would reach 93 cm.

Because the Moon's tidal forces drive the oceans with a period of about 12.42 hours (half of the Moon's synodic period of rotation), which is considerably less than the natural period of the oceans, complex resonance phenomena take place. The global average tidal lag is 12 minutes, which corresponds to an angle of 3 degrees between the position of the moon and the location of global average high tide. Tidal lag and the transfer of momentum between sea and land causes the Earth's rotation to slow down and the Moon to be moved further away in a process known as tidal acceleration.

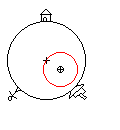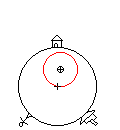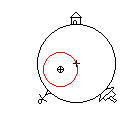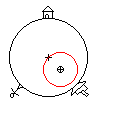
Some other explanations in articles on the physics of tides include the (apparent) centrifugal force on the Earth in its orbit around the common center of mass (the barycenter) with the Moon. The barycenter is located at about ¾ of the radius from the Earth's center. It is important to note that the Earth has no "rotation" around this point. It just "displaces" around this point in a circular way (see figure). Every point on Earth has the same angular velocity and the same radius of orbit, but with a displaced center. So the centrifugal force is uniform and does not contribute to the tides. However, this uniform centrifugal force is just equal (but with opposite sign) to the gravitational force acting on the center of mass of Earth. So subtracting the gravitational force at the center of Earth from the local gravitational forces at the surface, has the same effect as adding the (uniform) centrifugal forces. Although these two explanations seem very different, they yield the same results.

Image: http://www.seafriends.org.nz/oceano/topextide.jpg (52KB)

The first well-documented mathematical explanation of tidal forces was given in 1687 by Isaac Newton in the Philosophiae Naturalis Principia Mathematica. However, there is some evidence that Hellenistic Greeks were able to explain tides in terms of a mathematical theory of gravity. Lucio Russo, an Italian scholar, makes this argument in his books Flussi e Riflussi (yet to be published in English) and La Rivoluzione Dimenticata (which has been translated into English as The Forgotten Revolution). Russo argues that the ancients had a more developed theory of gravity than has generally been acknowledged. For example, he exhibits excerpts from ancient texts indicating that Seleucus of Seleucia (II B.C.) devised a gravitational explanation to prove that the Earth revolves around the Sun, rather than vice versa.

Tidal flows are of profound importance in navigation and very significant errors in position will occur if tides are not taken into account. Tidal heights are also very important; for example many rivers and harbours have a shallow "bar" at the entrance which will prevent boats with significant draught from entering at certain states of the tide.

Tidal flow can be found by looking at a tidal chart or tidal stream atlas for the area of interest. Tidal charts come in sets, each diagram of the set covering a single hour between one high tide and another (they ignore the extra 24 minutes) and give the average tidal flow for that one hour. An arrow on the tidal chart indicates direction and two numbers are given: average flow (usually in knots) for spring tides and neap tides respectively. If a tidal chart is not available, most nautical charts have "tidal diamonds" which relate specific points on the chart to a table of data giving direction and speed of tidal flow.

Standard procedure is to calculate a "dead reckoning" position (or DR) from distance and direction of travel and mark this on the chart (with a vertical cross like a plus sign) and then draw in a line from the DR in the direction of the tide. Measuring the distance the tide will have moved the boat along this line then gives an "estimated position" or EP (traditionally marked with a dot in a triangle).

Nautical charts display the "charted depth" of the water at specific locations and on contours. These depths are relative to "chart datum", which is the level of water at the lowest possible astronomical tide (tides may be lower or higher for meteorological reasons) and are therefore the minimum water depth possible during the tidal cycle. "Drying heights" may also be shown on the chart. These are the heights of the exposed seabed at the lowest astronomical tide.

Heights and times of low and high tide on each day are published in "tide tables". The actual depth of water at the given points at high or low water can easily be calculated by adding the charted depth to the published height of the tide. The water depth for times other than high or low water can be derived from tidal curves published for major ports. If an accurate curve is not available, the rule of twelfths can be used. This approximation works on the basis that the increase in depth in the six hours between low and high tide will follow this simple rule: first hour - 1/12, second - 2/12, third - 3/12, fourth - 3/12, fifth - 2/12, sixth - 1/12.

In addition to oceanic tides, there are atmospheric tides as well as terrestrial tides (earth tides), affecting the rocky mass of the Earth. Atmospheric tides may be negligible for everyday phenomena, drowned by the much more important effects of weather and the solar thermal tides. However, there is no strict upper limit to the Earth's atmosphere, and the tidal pull increases with the distance from the Earth's centre. Theoretically, the Earth's atmosphere extends beyond the Roche limit of the Earth in the Moon's gravitational field. Since the outer extremely thin layers of the atmosphere are in equilibrium with the layers below, the long term effects may not be easily neglected. This means, if the extremely thin outer layers are steadily siphoned away, the material is re-supplied by lower layers, causing an altogether constant small loss of material.

The Earth's crust, on the other hand, rises and falls imperceptibly in response to the Moon's solicitation. The amplitude of terrestrial tides can reach about 55 cm at the equator (15 cm of which are due to the Sun), and they are nearly in phase with the Moon (the tidal lag is about two hours only).

While negligible for most human activities, terrestrial tides need to be taken in account in the case of some particle physics experimental equipments (Stanford online). For instance, at the CERN or SLAC, the very large particle accelerators are designed while taking terrestrial tides into account for proper operation. Indeed, despite their kilometre-range dimension, centimetric deformations might lead to their malfunctioning as a physics experimental apparatus. Among the effects that need to be taken into account are : circumference deformation for circular accelerators, particle beam energy.

Since tidal forces generate currents of conducting fluids within the interior of the Earth, they affect in turn the Earth's magnetic field itself.

The loss of rotational energy of the earth, due to friction within the tides, and the torque produced by the gravitational effects of the Sun and Moon on the tidal deformations of the earth's body are responsible for the slowdown of the earth's rotation and the increase of the distance to the Moon, see Tidal force.

Tsunamis, the large waves that occur after earthquakes, are sometimes called tidal waves, but have nothing to do with the tides. Other phenomena unrelated to tides but using the word tide are rip tide, storm tide, hurricane tide, and red tide. The term tidal wave appears to be disappearing from popular usage.

Wikimedia Commons has media related to Category:Tides.

• http://www.seafriends.org.nz/oceano/tides.htm More information about tides and their effects (6pp)
• http://www.seafriends.org.nz/oceano/waves.htm Wave theory, how waves work, tsunamis, internal waves and more (19pp)
• "Myths about Gravity and Tides" - an extended and revised version of the paper originally published in “The Physics Teacher” 37, October 1999, pp. 438 - 441.
• Misconceptions about tides
• Direct and opposite tides, from the Center for Operational Oceanographic Products and Services (This site uses the concept of centrifugal force; see the above link if you're interested in an extended comment on that.)
• Earth tides calculator
• On-line version of "Our Restless Tides" NOAA's dated practical & short introduction to tides.
• [1] Tidal misconceptions
• An interface design used to view a sequence of tidal graphs against the changing phases of the moon.
• An easy to understand lesson on tides

• Easytide
• WWW Tide and Current Predictor
• Tides.INFO: Tide predictions for the world
• XTide Tide Prediction Server (provides tide information for places (such as Africa) that is unavailable on many other websites)
• World Tides Predictor