Talk:Symmetrical components
| This article is rated C-class on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: | ||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||
by virute of their being decupled,symmetric components are releted to each other by the fosterque matrix.the matrix contains the expression for the three components in terms of "i",which is in fact a representation of the imaginary operator in mathematics. however,in this case the multiplication of a vector by the quantity shifts its phase by 120,and not 90 degrees as would have been expected to happen. the positive phase sequence always exists in a net work and in a multi phase system,the positive phase sequence isn the only sequence when a conditiuon of imbalance or fault occurs the negetive phase and the zero phase sequence arise. the negetive phase sequence is exactly in the opposite direction to the positive sequence.typically this can be formed by interchanging any two of the three terminals in an electrical device(with three phase connections).since the negetive phase sequence is oppposite in orientation,for an electrical load supplied with a supply the generated emf is exactly opposite and hence the representaion contains no emf source. the positive phase sequence,however is represented as a power source driving all the impedences/loads in the circuit. the zero sequence network comprises of three 'in phase components' typically theyu do not cause any torques i machines at5 standstill,but on rotation their equvalent torques may not result to zero.they chiefly arise during grond associated faluts.
Moved from article
[edit]I have a difficulty with the description of the postive, neagtive and zero sequence components. My understanding is that these terms are used to describe the sequence with which they rotate. This is not the same as their direction of rotation.
Thus the postive sequence set would sequence in the (conventional) order of RYB. The negative sequence set in the order RBY, whilst the zero sequence set have no sequence, ie they are in phase with each other.
I suggest that the author(s) of this article might like to review their contribution in this regard.
Ian Grant
Whitianga NZ
- I moved this commentary from the article. Since there's little to identify an individual phase, I don't know that a definitive decision can be made between two sets of phasors in the same phase sequence and opposite rotation, vs. two sets with the same rotation and opposing phase sequence. Is the distinction even meaningful? Physically I know that negative phase sequence currents give rise to motor torques that oppose the positive sequence, so to me it seems appealing to call them opposite rotation. --Wtshymanski 17:59, 25 August 2006 (UTC)
As stated in Blackburn (Para. 3.2.2, see article references), the phasor set always rotates counterclockwise (angle increasing) according to normal mathematical convention. The positive- and negative-sequence space vectors rotate in opposite directions, but these should not be confused with phasors. The phase sequence or rotation is the order in which the phasors pass the axis with increasing time (the sequence of maximum voltages). This means that for normal a-b-c sequence, the sequence is from a clockwise to b, then clockwise to c. As a machine designer, I usually visualize the space vectors.
Allen Windhorn Kasota, Minn. USA
- I agree with Allen Windhorn. In any textbook on Circuit Analysis/Theory, in both positive/abc and negative/acb phase sequence, the phasors rotate in counterclockwise direction. This is because the argument of the sinors (a sinor is a phasor times the factor , as explained in Alexander & Sadiku's Fundamentals of Electric Circuits) increases positively since and also in the real world. And as we know, the convention in vector analysis and geometry is to measure positive angles in the counterclockwise direction. --Alej27 (talk) 18:49, 18 June 2021 (UTC)
Needs a diagram
[edit]One picture worth 1000 words in this case. Show one example of an unbalanced set of phasors and the three balanced sets that add up to create it. --Wtshymanski (talk) 21:16, 24 March 2010 (UTC)
I added a diagram that somewhat addresses the issue brought up by the user above, but it is by no means perfect. An animation would also be nice: I imagined it as the unbalanced three-phase system evolving with time along with the rotating symmetrical component vectors Kashyap.valiveti (talk) 15:22, 27 November 2013 (UTC)
I added an animation of the effect on the symmetrical components of increasing the phase angle of one phase. There are two .gifs, one showing the voltage phases and one showing the resulting symmetrical components. New to Wikipedia, so not sure how to put them into one box, but that would be more desirable. Mbariya (talk) —Preceding undated comment added 05:33, 10 December 2015 (UTC)
- Thanks for creating and uploading those illustrations, Mbariya. Great job! I put them into one box using template:multiple image.[1] Dalba 06:24, 10 December 2015 (UTC)
Possible mistake in the first paragrah.
[edit]Hello. The first paragraph in this article states that "the method of symmetrical components is used to simplify analysis of unbalanced three phase power systems".
However, I am reading the book Fundamentals of power quality, by Surya Santoso, and in the symmetrical components section it states that "The use of the symmetrical components method assumes that the circuit prior to the short-circuit condition is balanced". Based on this statement I think there is a discrepancy in the article. —Preceding unsigned comment added by Rangel alex (talk • contribs) 13:04, 4 June 2010 (UTC)
Nevermind, I did a little more research and it is correct.
Rangel alex (talk) 13:19, 4 June 2010 (UTC)
Font style confusing
[edit]Phasors (which are complex numbers) use the same font as vectors of phasors, making them difficult to distinguish. Comfr (talk) 19:24, 10 November 2016 (UTC)
- I changed the vectors to boldface. Comfr (talk) 03:05, 12 November 2016 (UTC)
Also, the article talks about symmetrical components and sequence components, without identifying the relationship. Comfr (talk) 20:16, 10 November 2016 (UTC)
- I have attempted to clarify components and sequences. Comfr (talk) 18:54, 12 November 2016 (UTC)
Sequence wrong?
[edit]
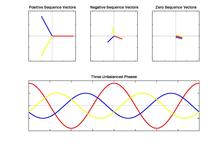
SymmComponents.gif shows the phases as RBG for both the positive sequence as well as the negative sequence. Shouldn't the negative sequence be RGB?
In contrast, unbalanced symmetrical components.pdf shows RYB for the positive sequence, but RBY for the negative sequence. Comfr (talk) 03:53, 11 November 2016 (UTC) Three Phase Case: There does seem to be a problem with the positive and negative phase sequence animations. They appear identical. It seems when the blue sine wave is phased correctly, negative sequence voltage should be minimum and positive phase sequence voltage should be maximum. Having them track each other lacks expression of one detracting from the other.Jeffreagan (talk) 22:49, 29 May 2018 (UTC)
- Yes, it is definitely wrong. As it stands it's more confusing than helpful. Have removed. StuartH (talk) 08:06, 10 January 2019 (UTC)
Harmonics and symmetrical components? Isn't that contradictory/invalid/wrong?
[edit]While harmonics can be present in linear circuits if the sources already have harmonics, when we talk about harmonics, we usually mean in non-linear circuits where the sources are sinusoidal with one same frequency. The section Contribution of harmonics to symmetrical components in 3-phase power systems of this article talks about harmonics and symmetrical components. Isn't that contradictory/invalid/wrong? I say this because Fortescue's theorem is based on superposition theorem, which is valid only for linear circuits/power systems. Just to back-up my point, this webpage from Wiley says in section 9 that “[…] the results of Fortescue […] are proven by the superposition theorem, and for this reason, a direct generalization to nonlinear networks is impossible.” Thus, we can’t apply Fortescue’s theorem (symmetrical components) to non-linear power systems or circuits, at least not directly. So why do engineers talk about symmetrical components (which is valid for linear networks) combined with harmonics (which occur in non-linear networks, thus the contradiction)?
The only valid reason I can think of is that if the non-linear power system is approximated by a linear one, then the theorem would be valid as long as the linear approximation is valid. --Alej27 (talk) 01:24, 31 October 2020 (UTC)
Questions about the section Poly-phase case
[edit]In section Poly-phase case of the current version of the article, it says "the transformation matrix above is a discrete Fourier transform". Does it refer to the matrix? Also, what does it mean "a DFT"? I mean, are there various DFTs?
And, why is the matrix a DFT? DFT is used to represent discrete-time periodic signals for all time (or the periodic extension of aperiodic signals in the time interval where the DFT is computed) using a finite number of different harmonically related discrete sinusoids. What does this have to do with Fortescue's theorem, which is used for a set of three continuous-time unbalanced (i.e. of same frequency but different amplitude and not phase-shifted in time by 120° between each other) sinusoidal signals? --Alej27 (talk) 18:16, 18 June 2021 (UTC)







