Sheffer stroke: Difference between revisions
m →Introduction, elimination, and equivalencies: Corrected own mistake. |
Rm diagram; these have been discussed at length, and have never gained support |
||
| Line 87: | Line 87: | ||
</tr> |
</tr> |
||
</table> |
</table> |
||
The following [[Hasse diagram]] shows all binary [[logical connective]]s expressed with the NAND operator, represented by the red circle: |
|||
<imagemap>Image:Logical connectives expressed with NAND.svg|thumb|left|800px|Logical connectives expressed with NAND. Move your mouse over the graphic to see their names. <small>[[:File:Logical connectives expressed with NAND.svg|(file)]]</small> |
|||
circle 495 371 40 [[Proposition (philosophy)|A]] |
|||
circle 668 370 40 [[Proposition (philosophy)|B]] |
|||
circle 249 370 40 [[Negation|not (A)]] |
|||
circle 76 370 40 [[Negation|not (B)]] |
|||
circle 372 668 40 [[Contradiction|contradiction]] |
|||
circle 371 73 40 [[Tautology (logic)|tautology]] |
|||
circle 371 248 40 [[Exclusive or|XOR (A,B)]] |
|||
circle 372 494 40 [[Logical biconditional|XNOR (A,B)]] |
|||
circle 163 581 40 [[Logical NOR|NOR (A,B)]] |
|||
circle 286 458 40 [[Material nonimplication|nonimplication (A,B)]] |
|||
circle 459 457 40 [[Converse nonimplication|converse nonimplication (A,B)]] |
|||
circle 581 581 40 [[Logical conjunction|AND (A,B)]] |
|||
circle 162 161 40 [[Sheffer stroke|NAND (A,B)]] |
|||
circle 286 284 40 [[Converse implication|converse implication (A,B)]] |
|||
circle 459 284 40 [[Material implication|implication (A,B)]] |
|||
circle 580 161 40 [[Logical disjunction|OR (A,B)]] |
|||
desc none |
|||
</imagemap> |
|||
<br clear=all> |
|||
==Formal system based on the Sheffer stroke== |
==Formal system based on the Sheffer stroke== |
||
Revision as of 21:05, 1 June 2009
| INPUT | OUTPUT | |
| A | B | A NAND B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
The Sheffer stroke, written "|" (see vertical bar) or "↑", in the subject matter of boolean functions or propositional calculus, denotes a logical operation that is equivalent to the negation of the conjunction operation, expressed in ordinary language as "not both". It is also called the alternative denial, since it says in effect that at least one of its operands is false. In Boolean algebra and digital electronics it is known as the NAND operation ("not and").
Like its dual, the NOR operator (a.k.a. the Peirce arrow or Quine dagger), NAND can be used by itself, without any other logical operator, to constitute a logical formal system (making NAND functionally complete). This property makes the NAND gate crucial to modern digital electronics, including its use in NAND flash memory and computer processor design.
Definition
The NAND operation is a logical operation on two logical values, typically the values of two propositions, that produces a value of false if and only if both of its operands are true. In other words, it produces a value of true if and only if at least one of its operands is false.
Truth table
The truth table of p NAND q (also written as p | q or p ↑ q) is as follows:
| p | q | ↑ |
|---|---|---|
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | T |
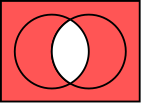
Venn diagram
The Venn Diagram of "A nand B" (the red area is the area covered by NAND).
History
The stroke is named after Henry M. Sheffer, who proved (Sheffer 1913) that all the usual operators of propositional logic (not, and, or, implies, and so on), could be expressed in terms of it. Charles Sanders Peirce (1880) had discovered this fact more than 30 years earlier, but never published his finding. Peirce also observed that all boolean operators could be defined in terms of the NOR operator, the dual of NAND.
Properties
Nand does not possess any of the following five properties, each of which is required to be absent from at least one member of a set of functionally complete operators: truth-preservation, falsity-preservation, linearity, monotonicity, self-duality. An operator is truth- (falsity-) preserving if its value is truth (falsity) whenever all its arguments are truth (falsity).
Symbol
One way of expressing p NAND q is as , where the symbol signifies AND and the line over the expression signifies not, the logical negation of that expression.
Natural language/rhetoric/colloquial usage
NAND is not used in everyday sentences because it exhibits an inherent inversion, which makes it confusing like a double negative. Here's an example of a sentence using:
- NAND operator: We will surely die if we have food nand water.
- Common terms: We will surely die if we do not have both food and water.
- Or, by DeMorgan's Law: We will surely die if we lack either food or water.
Introduction, elimination, and equivalencies
The Sheffer stroke "|" is equivalent to the negation of conjunction:
Expressed in terms of NAND, the usual operators of propositional logic are:
| "not p" is equivalent to "p NAND p" | |
| "p and q" is equivalent to "(p NAND q) NAND (p NAND q)" | |
| "p or q" is equivalent to "(p NAND p) NAND (q NAND q)" | |
| "p implies q" is equivalent to "p NAND (q NAND q)" |
Formal system based on the Sheffer stroke
The following is an example of a formal system based entirely on the Sheffer stroke, yet having the functional expressiveness of the propositional logic:
Symbols
pn for natural numbers n
( | )
The Sheffer stroke commutes but does not associate. Hence any formal system including the Sheffer stroke must also include a means of indicating grouping. We shall employ '(' and ')' to this effect.
We also write p, q, r, … instead of p0, p1, p2.
Syntax
Construction Rule I: For each natural number n, the symbol pn is a well-formed formula (wff), called an atom.
Construction Rule II: If X and Y are wffs, then (X|Y) is a wff.
Closure Rule: Any formulae which cannot be constructed by means of the first two Construction Rules are not wffs.
The letters U, V, W, X, and Y are metavariables standing for wffs.
A decision procedure for determining whether a formula is well-formed goes as follows: "deconstruct" the formula by applying the Construction Rules backwards, thereby breaking the formula into smaller subformulae. Then repeat this recursive deconstruction process to each of the subformulae. Eventually the formula should be reduced to its atoms, but if some subformula cannot be so reduced, then the formula is not a wff.
Calculus
All wffs of the form
- ((U|(V|W))|((Y|(Y|Y))|((X|V)|((U|X)|(U|X)))))
are axioms. Instances of
- (U|(V|W)), U W
are inference rules.
Simplification
Since the only connective of this logic is |, the symbol | could be discarded altogether, leaving only the parentheses to group the letters. A pair of parentheses must always enclose a pair of wffs. Examples of theorems in this simplified notation are
- (p(p(q(q((pq)(pq)))))),
- (p(p((qq)(pp)))).
The notation can be simplified further, by letting
- (U) := (UU)
- ((U)) U
for any U. This simplification causes the need to change some rules:
- More than two letters are allowed within parentheses.
- Letters or wffs within parentheses are allowed to commute.
- Repeated letters or wffs within a same set of parentheses can be eliminated.
The result is a parenthetical version of the Peirce existential graphs.
Another way to simplify the notation is to eliminate parenthesis by using Polish Notation. For example, the earlier examples with only parenthesis could be rewritten using only strokes as follows
- (p(p(q(q((pq)(pq)))))) becomes
- |p|p|q|q||pq|pq, and
- (p(p((qq)(pp)))) becomes,
- |p|p||qq|pp.
This follows the same rules as the parenthesis version, with opening parenthesis replaced with a Sheffer stroke and the (redundant) closing parenthesis removed.
See also
References
- Charles Peirce, 1880. 'A Boolean Algebra with One Constant'. In Hartshorne, C, and Weiss, P., eds., (1931-35) Collected Papers of Charles Sanders Peirce, Vol. 4: 12-20. Harvard University Press.
- H. M. Sheffer, 1913. "A set of five independent postulates for Boolean algebras, with application to logical constants," Transactions of the American Mathematical Society 14: 481-488.