Ähnlichkeitssätze

Die Ähnlichkeitssätze sind Sätze, die hinreichende Bedingungen stellen, dass zwei Dreiecke zueinander ähnlich sind. Viele Aussagen der Geometrie lassen sich mit Hilfe der Ähnlichkeit von Dreiecken beweisen.

Die vier Ähnlichkeitssätze für Dreiecke lauten:

• Zwei Dreiecke sind zueinander ähnlich, wenn sie in zwei (und somit in drei) Winkeln übereinstimmen. (W:W:W-Satz)

• Zwei Dreiecke sind zueinander ähnlich, wenn sie in allen Verhältnissen entsprechender Seiten übereinstimmen. (S:S:S-Satz)

• Zwei Dreiecke sind zueinander ähnlich, wenn sie in einem Winkel und im Verhältnis der anliegenden Seiten übereinstimmen. (S:W:S-Satz)

• Zwei Dreiecke sind zueinander ähnlich, wenn sie im Verhältnis zweier Seiten und in dem der größeren Seite gegenüberliegenden Winkel übereinstimmen. (S:S:W-Satz)

Siehe auch: Kongruenzsätze

In den folgenden vier Abbildungen sind jeweils zwei ähnliche Dreiecke ABC und A’B’C’ – anschaulich gesprochen – „ineinander geschachtelt“.

Dann ist jedes Seitenlängenpaar in ABC quotientengleich zu dem entsprechenden Seitenlängenpaar in A’B’C’.

• 
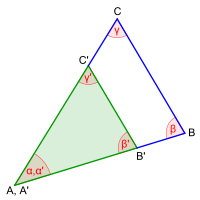
  W:W:W-Satz
  drei Winkel stimmen überein
• 
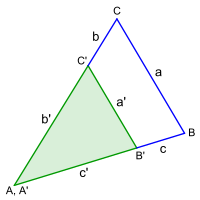
  S:S:S-Satz
  a : a' = (b + b') : b' = (c + c') : c'
• 
  S:W:S-Satz
  a : a' = (b + b') : b',
  die eingeschlossenen Winkel (γ, γ') stimmen überein
• 
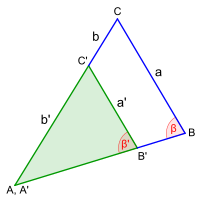
  S:S:W-Satz
  a : a' = (b + b') : b',
  die den größeren Seiten gegenüberliegenden Winkel (β, β') stimmen überein

• Alle gleichseitigen Dreiecke sind nach dem S:S:S-Satz zueinander ähnlich.
• Alle gleichschenklig-rechtwinkligen Dreiecke sind nach dem S:W:S-Satz zueinander ähnlich.
• Alle Dreiecke im Pythagoras-Baum sind zueinander ähnlich.

Gegeben seien ein Punkt ${\displaystyle P}$ innerhalb eines Dreiecks ${\displaystyle ABC}$ mit ${\displaystyle a=|BC|}$, ${\displaystyle b=|AC|}$ und ${\displaystyle c=|AB|}$ sowie die Parallelen durch ${\displaystyle P}$ zu den Dreiecksseiten. Diese Parallelen teilen jede Dreiecksseite in drei Abschnitte auf (siehe Planfigur).

Sind ${\displaystyle a'}$, ${\displaystyle b'}$ und ${\displaystyle c'}$ die Längen der jeweils mittleren Streckenabschnitte, so gilt:

${\displaystyle {\frac {a'}{a}}+{\frac {b'}{b}}+{\frac {c'}{c}}=1}$.

Der Beweis resultiert aus der Ähnlichkeit der drei grauen Dreiecke zum Dreieck ${\displaystyle ABC}$. Hieraus ergibt sich zunächst

${\displaystyle {\frac {b'}{s}}={\frac {b}{c}}}$ und ${\displaystyle {\frac {a'}{t}}={\frac {a}{c}}}$

und danach durch Umformung

${\displaystyle {\frac {b'}{b}}={\frac {s}{c}}}$ und ${\displaystyle {\frac {a'}{a}}={\frac {t}{c}}}$

Daraus folgt schließlich

${\displaystyle {\frac {a'}{a}}+{\frac {b'}{b}}+{\frac {c'}{c}}={\frac {t}{c}}+{\frac {s}{c}}+{\frac {c'}{c}}=1}$.^[1]

• Hans Schupp: Elementargeometrie. UTB, Stuttgart 1977. ISBN 3-506-99189-2, S. 144
• Elke Warmuth: Strahlensätze und Ähnliches, Vorlesung Sommersemester 2018 an der Humboldt-Universität zu Berlin (Steckbrief), PDF-Dokument, abgerufen am 9. Dezember 2022
• Joseph D. E. Konhauser, Dan Velleman, Stan Wagon: Which Way Did the Bicycle Go? Mathematical Association of America, Washington (1996)

1. ↑ Claudi Alsina, Roger B. Nelsen: Perlen der Mathematik - 20 geometrische Figuren als Ausgangspunkte für mathematische Erkundungsreisen, Springer Spektrum, Springer-Verlag GmbH Berlin 2015, ISBN 978-3-662-45460-2, Seite 56