图博弈论
外观
在博弈论中,描述博弈论的常用方法有正则形式的博弈和扩展形式的博弈。图博弈论是参与者之间简洁博弈的表示形式。
考虑一个博弈,有个参与者,每个人有种策略。我们将任何一个参与者表示为一个图中的节点,在这个图中,每个参与者都有一个效用函数,这个效用函数仅仅与其邻居有关。该效用函数依赖的其他参与者越少,图示也就越小。
形式定义
[编辑]博弈由图表示,其中每个参与者由图中的一个节点表示,当且仅当图中的两个节点和的效用函数相互依赖时,则它们之间有一条边。中的每个节点有一个函数,其中是顶点的度数。是参与者���策略以及其邻居之策略的效用函数。
博弈规模的表示
[编辑]对于一个有个参与者的博弈,每个参与者有种可能的策略,博弈的规模就是。该博弈的图规模为,其中为图中最大节点度。如果,则图博弈规模远小于一般博弈的规模。
实例
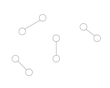
[编辑]当每个参与者的效用函数只依赖于另一个参与者时:
-
描述博弈的图
图的最大度为1,因此博弈可以用个大小为的图表示,所以总大小是.
纳什均衡
[编辑]找到纳什均衡所需时间与图的大小呈指数相关。如果图博弈的图是树,只需多项式时间就能找到纳什均衡。如果最大的节点度数大于3,这个问题就是NP完全问题。
延伸阅读
[编辑]- Michael Kearns (2007) "Graphical Games (页面存档备份,存于互联网档案馆)".
- Michael Kearns, Michael L. Littman and Satinder Singh (2001) "Graphical Models for Game Theory (页面存档备份,存于互联网档案馆)".