Секторна діаграма
| Секторна діаграма | |
 | |
| Підтримується Вікіпроєктом | Вікіпедія:Проєкт:Математика |
|---|---|
| | |

Секторна діаграма або Кругова діаграма — один із статистичних графіків у формі кола, який поділений на сегменти, що ілюструють чисельне співвідношення. У секторній діаграмі, довжина кривої кожного сегменту(а отже і його центральний кут та площа), відповідає числу, яке вона зображує. Незважаючи на те, що англійський варіант (pie chart) отримав свою назву через надзвичайну схожість с пирогом, який ділять на шматки, зовнішній вигляд секторної діаграми може бути різним. Найпершою секторною діаграмою ми завдячуємо Вільяму Плейферу та його «Скороченому викладу статистики».
Секторні діаграми дуже широко застосовуються у бізнесі та засобах масової інформації. Хоча багато хто їх критикує та велика кількість фахівців рекомендують уникати їх, посилаючись на дослідження, що показали як важко порівнювати сегменти секторної діаграми, або зіставляти дані з різних секторних діаграм. Секторні діаграми у більшості випадків можуть бути замінені на інші графіки, такі як стовпчикові діаграми, коробковий графік та точкові графіки.
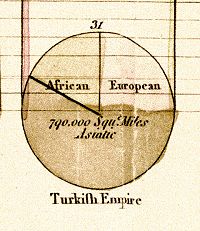
Найпершою відомою секторною діаграмою ми завдячуємо Вільяму Плейферу та його праці Скорочений виклад статистики, що вийшла у 1801 році, де використані такі два графіки. Плейфер навів приклад, у яких були використані секторні діаграми. Один з тих графіків зображував співвідношення народів Османської імперії, розташованих в Азії, Європі та Африці до 1789 року. Спочатку його інновація не набула широкого застосування.
| Ранні типи секторних діаграм в 19-му столітті | ||||||||
|---|---|---|---|---|---|---|---|---|
|
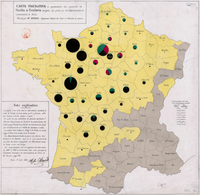
Французький інженер Чарльз Джозеф Мінар був одним із перших, хто використовував секторні діаграми в 1858 році, зокрема, на мапах. Мапа Мінара, виконана в 1858 році. Тут автор використав секторні діаграми, для того, щоб зообразити кількість худоби, яку надсилали з усієї Франції для споживання у Парижі (1858).
Плейфер вважав, що для того, щоб секторні діаграми могли давати додаткову інформацію їм потрібно було б мати третій вимір. Вважалося, що Флоренс Найтінгейл винайшла цей третій вимір, однак насправді вона лише популяризувала його. Пізніше припускалося, що вона вигадала своє трактування третього виміру через незрозумілість відкриття Плейфера.
Тривимірна секторна діаграма використовується для того, щоб надати графіку об'ємного виду. Найчастіше така діаграма використовується з естетичних міркувань, оскільки третій вимір не покращує процес пізнання даних- навпаки, такі графіки важко тлумачити через спотвореного ефекту перспективи, який асоціюється із третім виміром. Застосування додаткових вимірів, що не використовуються для відображення необхідної інформації, не вважається необхідним не тільки для секторних діаграм, але й для графіків у цілому.

Кругова (насправді кільцева) діаграма являє собою варіант секторної діаграми із пустим центром дозволяє отримати додаткову інформацію про дані в цілому. які необхідно відмітити на графіку.

Приклад секторної діаграми з розділеннями (нижче) з відділенням найбільших політичних кампаній. Графік із одним або декількома сегментами, відокремленими від решти секторної діаграми називається секторною діаграмою з розділеннями. Цей засіб використовується для того, щоб підкреслити сектор, або, виділити менші сектори діаграми з невеликими процентними співвідношеннями.

Діаграма сонячного випромінювання дуже схожа зі звичайною секторною діаграмою, за винятком того, що сектори мають однакові кути та відрізняються лише тим, на скільки кожен сегмент віддалений від центру кола. Діаграма сонячного випромінювання використовується для побудови повторюваних явищ (наприклад, кількість смертей у кожному місяці). Наприклад, якщо Ви хочете зробити графік кількості смертей в кожному місяці протягом року, тоді необхідно побудувати 12 секторів (по одному на місяць) з однаковим кутом в 30 градусів. Радіус кожного сектора буде пропорційним квадратному кореню з підрахунку смерті за місяць, так що площа сектора дорівнюватиме числу смертей за місяць. Якщо кількість смертей в кожному місяці відрізняється за причинами смерті, то можна зробити декілька порівнянь на одному графіку, як це видно на діаграмі сонячного випромінювання, що була створена Флоренс Найтінгейл.
Перше відоме використання діаграм сонячного випромінювання було завдяки Андре-Мішелю Гері: свій графік він назвав courbes circulaires, у документі, що налічує 1829 сторінок, що показує сезонні і добові зміни напрямку вітру протягом року, а також кількість народжень і смертей кожної години дня. Леон Лаланн пізніше використовували діаграму сонячного випромінювання для того, щоб у 1843 році показати частоту напрямку вітру біля точок компаса. Роза вітрів досі використовується метеорологами. Найтінгейл опублікував її графік рози вітрів у 1858 році. Слово «фат» іноді використовується помилково: це була назва, яку Найтінгейл використовував для посилання на книгу, що містила діаграми, а не самих графіків. Було висловлено припущення нібито більшість ранньої слави Найтінгейл була заснована на її здатності давати чіткі і стислі виклади даних.

Кільцева діаграма, також відома як багаторівнева секторна діаграма використовується для зображення ієрархічних даних, втілених у вигляді концентричних кіл. Коло в центрі являє собою поняття, що лежить в основі даних, які ієрархічно розповсюджуються від центру діаграми. Сегмент внутрішнього кола має ієрархічні відношення з секторами зовнішнього кола, які лежать у межах кута щойно названого сегменту.
Одним із можливих варіантів діаграми сонячного випромінювання можна назвати ієрархічну секторну діаграму. Цей графік накладає звичайну секторну діаграму з дещо зміненою діаграмою сонячного випромінювання для того, щоб зробити порівняння двох наборів даних, пов'язаних між собою. Базова секторна діаграма — перший набір даних у звичайному вигляді з сегментами різних розмірів. Другим набором є накладена діаграма сонячного випромінювання, у якій використовуються ті ж самі кути, як і в основній, та застосовуються радіуси, за допомогою яких регулюється зміст та обсяг інформації. Наприклад, базова секторна діаграма може показати розподіл вікових і статевих груп у населенні, а також накладання кількості їх фігурування у дорожніх аваріях. Вік та стать групи, які найчастіше потрапляють у нещасні випадки виділяються як сегменти, що виступають за межі початкового графіку секторної діаграми.
Квадратні діаграми є непересічною формою секторних діаграм, у яких замість кіл використовуються квадрати, які представляють відсоткове співвідношення. Аналогічно основними секторним діаграмам, квадратні секторні діаграми приймають основне поняття чи загальну кількість за 100 %.

У наступному прикладі діаграма базується на попередніх результатах виборів до Європейського парламенту 2004 року. В таблиці вказано кількість місць, виділених для кожної партії, а також відсоток. який вони складають із цілого числа. Значення в останньому стовпці дорівнює значенню центрального кута кожного сегмента, визначається шляхом множення відсоток на 360 °.
| Група | Кількість місць | Відсоток (%) | Центральний кут (°) |
|---|---|---|---|
| EUL | 39 | 5,3 | 19,2 |
| ПЕС | 200 | 27,3 | 98,4 |
| ОДВ | 42 | 5,7 | 20,7 |
| EDD | 15 | 2,0 | 7,4 |
| ЄЛДР | 67 | 9,2 | 33,0 |
| EPP | 276 | 37,7 | 135,7 |
| UEN | 27 | 3,7 | 13,3 |
| Інші | 66 | 9,0 | 32,5 |
| Разом | 732 | 99,9 * | 360,2 * |
- Через округлення, ці підсумки не додаються до 100 і 360.
Градусна міра кожного центрального кута пропорційна кількості відповідної величини, тут число місць. Так як сума центральних кутів повинна дорівнювати 360 °, центральний кут для кожної величини є частиною Q від загального обсягу 360Q градусів. У прикладі, центральний кут для найбільшої групи (Європейська народна партія (ЄНП)) становить 135,7 °, тому що 0,377 помножити на 360, округлене до одного знака після коми, дорівнює 135,7.
Очевидним недоліком секторних діаграми є те, що вони не можуть показати більше, ніж кілька значень без розділення візуального кодування (далі «сегментів») з даних, які вони представляють (як правило, відсотки). Коли сегменти стають занадто малими, секторні діаграми повинні відрізнятися кольорами, текстурами або мати стрілки так, щоб читач міг зрозуміти графіки. Такі деталі роблять діаграми непридатними для роботи із великими обсягами даних. Секторні діаграми також займають багато простору на сторінці в порівнянні з більш гнучкими гістрограмами, яким непотрібно мати додаткові підписи та які можуть показувати інші значення, такі як сеердні величини або контрольні цифри одночасно.
Статистики в цілому розглядають секторні діаграми, як поганий метод відображення інформації, і вони є рідкістю в науковій літературі. Однією з причин цього є те, що дуже важко виконати порівняння між об'єктами в діаграмі, оскільки поняття площа використовується замість слова довжина, та коли різні об'єкти показані як різні форми.

Крім того, в дослідженнях, проведених в AT&T Bell Laboratories, було показано, що порівняння за кутом виявилося менш точним, ніж порівняння за довжиною. Це може бути проілюстровано на прикладі сусіднього графіку, що зоображує три секторні діаграми, та, під кожною з них розташована відповідна гістограма, яка використовує ті ж самі дані. У багатьох предметах виникають труднощі з розподілом сегментів за розмірами. Набагато легше використовувати г��стограми для порівняння даних. Ааналогічно, порівнювати набори даних набагато легше за допомогою гістограм. Однак, якщо мета полягає в тому, щоб порівняти дану категорію (сегмент графіку) із загальною кількістю (діаграма в цілому) в одному графіку та НСК близький до 25 або 50 відсотків, тоді секторна діаграма може бути набагато еффективнішою, аніж гістограма.

Приклад (ліворуч) - секторна діаграма із 18 значеннями, у якому інформацію треба розділити від її зображення. Зауважте також, що декілька значень позначені однаковим кольором, що ускладнює трактування графіку.
Кілька досліджень, представлених на Європейській конференції з візуалізації проаналізували відносну точність декількох форматів секторної діаграми та дійшли висновку, що у секторних та кругових діаграмах виникають однакові помилки при їх розумінні, а квадратні секторні діаграми забезпечують найточніше зображення даних на графіку.