Момент імпульсу
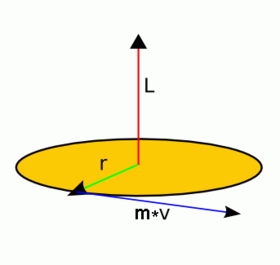
Моме́нт і́мпульсу (також: кутовий момент, момент кількості руху) — векторна величина, що характеризує величину та напрямок обертального руху тіла. Для матеріальної точки вона дорівнює векторному добутку радіус-вектора точки та її імпульсу .
| Момент імпульсу | |
 | |
| Розмірність | |
|---|---|
| Формула | [1][2] |
| Позначення у формулі | , і |
| Символ величини (LaTeX) | [2] |
| Підтримується Вікіпроєктом | Вікіпедія:Проєкт:Математика |
| Рекомендована одиниця вимірювання | kilogram square metre per secondd[2][3] |
 | |
 | |
| | |
Момент імпульсу в класичній механіці
ред.| Зовнішні відеофайли | |
|---|---|
| 1. Що таке момент імпульсу (кутовий момент) // Канал «Цікава наука» на YouTube, 13 квітня 2021. | |
Визначення
ред.Моментом імпульсу матеріальної точки відносно початку координат в класичній механіці є псевдовектор, який дорівнює векторному добутку радіус-вектора даної точки та її імпульсу:
Відповідно,
- — момент імпульсу;
- — радіус-вектор;
- — імпульс.
Якщо фізична система складається з багатьох матеріальних точок, то результуючий момент імпульсу відносно початку координат є сумою (інтегралом) усіх моментів імпульсу складових системи.
Для багатьох практичних задач, які вивчають властивості об'єкта, що обертається навколо певної осі, достатньо проаналізувати скалярне значення моменту імпульсу , яке є проєкцією вектора моменту імпульсу на дану вісь і може бути як додатним, так і від'ємним. Ця величина також називається моментом імпульсу відносно осі. Відповідно до визначення векторного добутку векторів, скаляр моменту імпульсу визначається як
- ,
де та — проєкції векторів та на площину, що перпендикулярна даній осі, — кут між та , який вимірюється від до ; такий порядок обходу векторів при визначенні кута є принциповим. Якщо порядок змінити на зворотний, зміниться й знак.
Для тіла сталої маси, яке обертається навколо фіксованої осі, момент імпульсу можна визначити як добуток моменту інерції тіла відносно цієї осі та кутової швидкості обертання тіла:
- ,
де — скалярний момент інерції, — вектор кутової швидкості. У випадку довільного обертання величина є тензором другого рангу і називається тензором інерції. Тоді може бути непаралельним до .
Момент імпульсу у Спеціальній теорії відносності та класичній теорії поля
ред.У Спеціальній теорії відносності вектор моменту імпульсу дає компоненти антисиметричного тензора другого рангу — тензора моменту імпульсу та спіну:
,
або, у явному вигляді,
,
де — вектори моменту імпульсу та спіну.
Тензорне представлення вектора моменту імпульсу виникає з того, що перетворення Лорен��а даного вектора збігається з перетворенням Лоренца компонент антисиметричного тензора.
У рамках класичної теорії поля тензором моменту імпульсу та спіну називають струм, який відповідає інваріантності лагранжіана поля щодо перетворень Лоренца, які можна інтерпретувати як повороти у 4-просторі-часі:
,
де — тензор енергії-імпульсу, — поле, — величина-похідна, що визначає трансформаційні властивості поля щодо перетворення Лоренца.
Наявність спінової частини у тензорі моменту імпульсу та спіну тісно пов'язано із симетрією тензора енергії-імпульсу відносно перестановки індексів. Якщо тензор енергії-імпульсу симетричний, то кутова та спінова частини тензора моменту імпульсу та спіну зберігаються (у термінах теорії поля) окремо. Якщо ж провести процедуру "занесення" спінової частини до кутової тензору моменту імпульсу та спіну, то одночасно із цим можна симетризувати тензор енергії-імпульсу. Така процедура називається процедурою Беліфанте.
Закон збереження моменту імпульсу
ред.Момент імпульсу — одна з фізичних величин, для якої діє фундаментальний закон збереження.
Назвемо замкненою (в сенсі обертання) таку систему, для якої сума моментів зовнішніх сил дорівнює нулю. Для такої системи
- ,
звідки
- .
Тобто, в замкненій системі момент імпульсу зберігається незмінним. Як випливає з теореми Нетер, таке твердження є наслідком ізотропності (тобто рівноцінності всіх напрямів) простору.
Момент імпульсу у квантовій фізиці
ред.В квантовій механіці момент імпульсу визначається не як фізична величина, а як оператор над вектором стану.
Оператор моменту імпульсу має вигляд:
де r та p — оператори радіус-вектора та імпульсу системи.
Для вільної частинки без спіну та електричного заряду, оператор моменту імпульсу може бути наведений в такій формі:
- , де — оператор Гамільтона.
Окремі компоненти оператора моменту імпульсу не комутують між собою. Внаслідок цього їх неможливо визначити одночасно. Детальніше дивись в статті оператор кутового моменту.
Див. також
ред.Примітки
ред.- ↑ 4-12 // Quantities and units—Part 4: Mechanics — 1 — ISO, 2006. — 24 p.
- ↑ а б в 4-11 // Quantities and units — Part 4: Mechanics — 2 — ISO, 2019. — 15 с.
- ↑ 4-12.a // Quantities and units—Part 4: Mechanics — 1 — ISO, 2006. — 24 p.
Джерела
ред.- Єжов С. М., Макарець М. В., Романенко О. В. Класична механіка. — К. : ВПЦ "Київський університет", 2008. — 480 с.
- Федорченко А. М. Теоретична механіка. — К. : Вища школа, 1975. — 516 с.
- Биденхарн Л., Лаук Дж. Угловой момент в квантовой физике. Теория и приложения. — М. : Мир, 1984. — Т. 1. — 302 с.
- Блохинцев Д. И. Основы квантовой механики. — М. : Наука, 1976. — 664 с.
- Боум А. Квантовая механика: основы и приложения. — М. : Мир, 1990. — 720 с.
- Варшалович Д. А., Москалев А. Н., Херсонский В. К. Квантовая теория углового момента. — Л. : Наука, 1975. — 441 с.
- Зар Р. Теория углового момента. О пространственных эффектах в физике и химии. — М. : Мир, 1993. — 352 с.






