Камень, ножницы, бумага
«Камень, ножницы, бумага» — популярная игра на руках, часто использующаяся как способ жеребьёвки для определения очерёдности хода или ведущего в других играх.
| Камень, ножницы, бумага | |
|---|---|
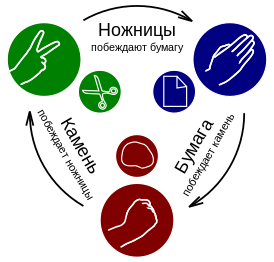 Схема, по которой выявляется победитель | |
| Инвентарь | нет |
| Игроков | 2+ |
| Длительность партии | ~3 секунды |
| Сложность правил | Очень низкая |
| Уровень стратегии | Низкий |
| Влияние случайности | Очень высокое |
Правила игры
правитьВ разделе не хватает ссылок на источники (см. рекомендации по поиску). |
Игроки считают вместе вслух «Камень… Ножницы… Бумага… Раз… Два… Три», одновременно качая кулаками. Существуют и другие варианты счёта, распространённость которых различается в разных городах и регионах, например, «Су-е-фа!» («Су-ли-фа»), «Рас(е)л-двас(е)л-трис(е)л!», «Пи-Ни-Ко!», «Эна-бена-цо!», «Ван-чу-фри», «Бу-це-фа», «Аль… ман… джуз!», «Чу-ва-чи», «Чи-чи-ко», «Е-ша-чёк», «Бу-ли-фа» и другие. На счёт «Три» они одновременно показывают при помощи руки один из трёх знаков: камень, ножницы или бумагу.
Победитель определяется по следующим правилам:
- Бумага побеждает камень («бумага обёртывает камень»).
- Камень побеждает ножницы («камень затупляет ножницы»).
- Ножницы побеждают бумагу («ножницы разрезают бумагу»).
Если игроки показали одинаковый знак, то засчитывается ничья и игра переигрывается.
В классическом варианте в игру играют вдвоём, однако возможна игра большего количества участников. При этом ничья засчитывается в ситуации, когда в компании игроков появились все три жеста (это иногда называют «кашей»), или если все игроки показали один и тот же знак.
История
правитьИгра была изобретена в Китае[1]. Согласно книге Уцзацзу (кит. трад. 五雜組 (五雜俎), упр. 五杂组 (五杂俎), пиньинь Wǔzázǔ), написанной Се Чжаочжэ (кит. трад. 謝肇淛, упр. 谢肇淛, пиньинь Xiè Zhàozhè) во времена поздней династии Мин, военачальники эпохи поздней династии Хань играли в игру, называемую шоушилин (кит. трад. 手勢令, упр. 手势令, пиньинь shǒushìlìng), которая признаётся эквивалентной современной «Камень, ножницы, бумага». Шоушилин может быть переведено как «команды рукой». Также существует японский вариант игры «дзян-кэн» (яп. じゃんけん) или «индзян» (яп. いんじゃん). Существует также японский вариант на основе сёги — じゃんけんしょうぎ.
Варианты
правитьДругие фигуры
правитьВ разделе не хватает ссылок на источники (см. рекомендации по поиску). |
В малайской версии игры птица > вода > камень > птица.
Реклама FedEx продемонстрировала игру медведь > ниндзя > охотник > медведь. Фигуры исполняются всем телом.
Больше фигур
правитьСуществует вариант «колодец, камень, ножницы, бумага» (предположительно родом из Франции; колодец топит ножницы и камень, и накрывается бумагой). Он ничем не отличается от стандартного — колодец доминирует над камнем, и остаются всего три Парето-эффективных стратегии: колодец > ножницы > бумага > колодец[источник не указан 224 дня].
Существуют несколько вариантов из пяти фигур. Один из них — «камень, ножницы, бумага, ящерица, Спок», изобретённый Сэмом Кассом и Карен Брила[2]. Он стал популярным благодаря американскому комедийному сериалу «Теория Большого взрыва». Правила игры описываются следующим образом:
Ножницы режут бумагу. Бумага заворачивает камень. Камень давит ящерицу, а ящерица травит Спока, в то время как Спок ломает ножницы, которые, в свою очередь, отрезают голову ящерице, которая ест бумагу, на которой улики против Спока. Спок испаряет камень, а камень, разумеется, затупляет ножницы.
По теории вероятностей в классическом варианте вероятность победы, проигрыша и переигровки — одинаковая: 1/3=0,333… = 33,3333…%. В усиленном варианте ситуация меняется: вероятность победы и проигрыша — по 40 % (+6,666…%), а переигровки — 20 % (−13,333…%). То есть если использовать улучшенный вариант инструмента разрешения споров, то в среднем количество нерезультативных раундов будет меньше.
Существует кросс-платформенная программа для игры в изобретённый Сэмом Кассом и Карен Брила вариант для DOS, Windows, MacOS, Linux, FreeBSD с открытым исходным кодом[3].
В некоторых местностях существуют варианты до 9 фигур[4].
С точки зрения теории игр
правитьВ разделе имеются утверждения, не подкреплённые источниками. |
Чтобы определить победителя, нужно в среднем 1,5 попытки — если, конечно, выбор игроков абсолютно случаен. Для определения победителя в игре из трёх игроков в среднем требуется 2,25 попытки.[5]
«Камень, ножницы, бумага» — матричная игра с нулевой суммой, у которой:
- Количество фигур (стратегий игроков) нечётно.
- Игра симметрична: обоим игрокам доступны одни и те же стратегии; если комбинация a-b выигрывает, то b-a проигрывает.
- Для любой фигуры a комбинация a-a даёт ничью. Из оставшихся n−1 фигур половина выигрывает над a (выигрыш 1), и половина проигрывает (выигрыш −1).
Назовём игру, подходящую под такое определение, «ОКНБ» (обобщённое камень-ножницы-бумага).
ОКНБ можно реализовать так: перенумеруем фигуры от 0 до n−1. Вычисляют разность по модулю . Если она равна 0 — ничья; из оставшихся n−1 разностей первые объявляются выигрышем первого или второго игрока произвольно, остальные — антисимметрично. Например, в игре «камень, бумага, ножницы, Спок, ящерица» (именно в таком порядке!) 1 выигрывает, 2 проигрывает — соответственно 4 проигрывает, 3 выигрывает. Камень (0) проигрывает Споку (3), потому что . Однако не все ОКНБ сводятся к разности по модулю: например, игроки бросают камень, ножницы и бумагу на двух руках; сравнивают левые руки, при ничьей — правые.
Равновесие по Нэшу в смешанных стратегиях у любого ОКНБ даёт вероятность для всех фигур. Другими словами, игра честна (если один игрок действует случайно, а второй независимо от него, ожидаемый выигрыш 0), нет «сильных» и «слабых» фигур, и выиграть можно лишь за счёт вещей, не связанных с теорией вероятностей: например, быстрой реакции на фигуру соперника или поиска неслучайных закономерностей в его выборе.
Игра с более мягкими требованиями — игра симметрична, комбинация a-a даёт ничью, у любой другой пары выигрыш ±1, и все фигуры Парето-эффективны — существует для всех n, кроме 2 и 4.[6] По этой причине к камню, ножницам и бумаге невозможно добавить четвёртую фигуру (колодец) без потери Парето-эффективности.
Игру упоминают в качестве примера для иллюстрации отсутствия свойства транзитивности.
Разное
правитьНесмотря на то, что исход идеальной игры случаен, при наличии определённых навыков игры с реальными противниками её исход можно предугадать, так как многие люди сознательно не действуют случайным образом или даже не могут этого. После нескольких игр можно распознать определённые неслучайные «паттерны» в поведении соперника, мало рефлексирующего над игрой[7][8]. Это связано также с тем, что во время второго раунда человек подсознательно показывает то, что могло победить его в прошлом. Так что если в первый раз противник показал «камень», то во второй раз целесообразно показывать «ножницы»: он, скорее всего, выберет «бумагу»[9][неавторитетный источник].
В 2013 году в Японии был сконструирован робот, побеждающий человека в «камень, ножницы, бумага» со стопроцентным результатом[10]. Выигрыш достигается не с помощью определённой стратегии, а за счёт анализа движений руки человека с помощью высокоскоростной камеры.
По игре проводятся чемпионаты мира со значительным призовым фондом, которые освещаются ведущими изданиями. Существует международная федерация и официальные правила проведения соревнований[11][12].
В настольных и компьютерных играх один из вариантов баланса называется «камень, ножницы, бумага»[13]. Поскольку четырёх фигур быть не может (см. выше), а сложность балансировки пропорциональна n², фигур обычно делают три или пять.
Перед матчем 8-го тура Чемпионата России по футболу 2021/2022 между командами «Крылья Советов» и «Ростовом», капитаны команд разыграли право стартового удара с помощью игры «Камень, ножницы, бумага», а не с помощью традиционного подбрасывания монеты[14].
Примечания
править- ↑ Moore, Michael E.; Sward, Jennifer (2006). Introduction to the game industry. Upper Saddle River, NJ: Pearson Prentice Hall. p. 535. ISBN 978-0-13-168743-1.
- ↑ Rock Paper Scissors Spock Lizard. Sam Kass Архивная копия от 13 ноября 2010 на Wayback Machine.
- ↑ R-P-S-L-S download | SourceForge.net. Дата обращения: 14 мая 2023. Архивировано 14 мая 2023 года.
- ↑ Камень, ножницы, бумага...: chuch666 — LiveJournal. Дата обращения: 23 апреля 2020. Архивировано 18 февраля 2018 года.
- ↑ Первая открытая Интернет-олимпиада по математике. Решение задачи 5.Камень, Ножницы, Бумага. Дата обращения: 8 августа 2014. Архивировано 10 августа 2014 года.
- ↑ How to Generalize Janken — Rock-Paper-Scissors-King-Flea — Springer. Дата обращения: 29 сентября 2017. Архивировано 1 февраля 2018 года.
- ↑ Dance, Gabriel and Jackson, Tom (7 октября 2010). "Rock-Paper-Scissors: You vs. the Computer". The New York Times. Архивировано 30 апреля 2011. Дата обращения: 15 июня 2011.
{{cite news}}:|archive-date=/|archive-url=несоответствие временной метки; предлагается 30 апреля 2011 (справка)Википедия:Обслуживание CS1 (множественные имена: authors list) (ссылка) - ↑ World RPS Society — How to beat anyone at Rock Paper Scissors. Дата обращения: 14 сентября 2012. Архивировано из оригинала 15 августа 2012 года.
- ↑ Ученые разгадали алгоритм выигрыша в «камень-ножницы-бумага». Дата обращения: 19 декабря 2007. Архивировано 14 сентября 2012 года.
- ↑ Японский робот научился выигрывать в игру «камень-ножницы-бумага». Дата обращения: 9 ноября 2013. Архивировано 9 ноября 2013 года.
- ↑ Сайт международной ассоциации игры Архивная копия от 15 сентября 2012 на Wayback Machine
- ↑ "UK Rock Paper Scissors Championship - Wacky Nation". Wacky Nation (англ.). Архивировано 14 ноября 2017. Дата обращения: 28 сентября 2017.
{{cite news}}:|archive-date=/|archive-url=несоответствие временной метки; предлагается 14 ноября 2017 (справка) - ↑ DTF.RU — Баланс возможностей в играх Архивная копия от 27 сентября 2007 на Wayback Machine
- ↑ Капитаны «Крыльев Советов» и «Ростова» разыграли право стартового удара с помощью игры «Камень, ножницы, бумага». Спорт-Экспресс. Дата обращения: 18 сентября 2021. Архивировано 19 сентября 2021 года.
В другом языковом разделе есть более полная статья Rock paper scissors (англ.). |