Teste Kolmogorov-Smirnov

Estatística
Estatísticos Notação Publicações de estatística Portal Categoria
v d e

Em estatística, o teste Kolmogorov–Smirnov (também conhecido como teste KS ou teste K–S) é um teste não paramétrico de bondade do ajuste sobre a igualdade de distribuições de probabilidade contínuas e unidimensionais que pode ser usado para comparar uma amostra com uma distribuição de probabilidade de referência (teste K–S uniamostral) ou duas amostras uma com a outra (teste K–S biamostral).^[1] Recebe este nome em homenagem aos matemáticos russos Andrei Kolmogorov e Nikolai Smirnov.

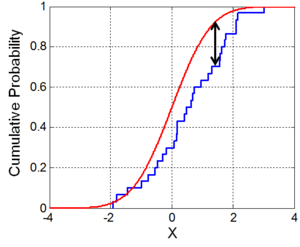
A estatística de Kolmogorov–Smirnov quantifica a distância entre a função distribuição empírica da amostra e a função distribuição acumulada da distribuição de referência ou entre as funções distribuição empírica de duas amostras. A distribuição nula desta estatística é calculada sob a hipótese nula de que a amostra é retirada da distribuição de referência (no caso uniamostral) ou de que as amostras são retiradas da mesma distribuição (no caso biamostral). Em cada caso, as distribuições consideradas sob a hipótese nula são distribuições contínuas, mas não restritas.

O teste K–S biamostral é um dos métodos não paramétricos mais úteis e difundidos para a comparação de duas amostras, já que é sensível a diferenças tanto no local, como na forma das funções distribuição acumulada empírica das duas amostras.^[2]

O teste de Kolmogorov–Smirnov pode ser modificado para servir como um teste da qualidade do ajuste. No caso especial do teste da normalidade da distribuição, as amostras são padronizadas e comparadas com uma distribuição normal padrão. Isto equivale a tornar a média e a variância da distribuição de referência iguais aos estimados da amostras, sabendo que usar isto para definir a distribuição de referência específica muda a distribuição nula da estatística. Vários estudos encontraram que, mesmo nesta forma corrigida, o teste é menos potente em avaliar a normalidade do que o teste de Shapiro–Wilk e o teste de Anderson–Darling.^[3] Entretanto, estes outros testes também têm suas desvantagens. O teste de Shapiro–Wilk, por exemplo, é conhecido por não funcionar bem em amostras com muitos valores idênticos.

A função distribuição empírica ${\displaystyle F_{n}}$ para ${\displaystyle n}$ observações ${\displaystyle X_{i}}$ independentes e identicamente distribuídas é definida como

${\displaystyle F_{n}(x)={1 \over n}\sum _{i=1}^{n}I_{[-\infty ,x]}(X_{i})}$

em que ${\displaystyle I_{[-\infty ,x]}(X_{i})}$ é a função indicadora, igual a 1 se ${\displaystyle X_{i}\leq x}$ e igual a 0 de outro modo.

A estatística de Kolmogorov–Smirnov para uma dada função distribuição acumulada ${\displaystyle F(x)}$ é

${\displaystyle D_{n}=\sup _{x}|F_{n}(x)-F(x)|}$

em que ${\displaystyle \sup _{x}}$ é o supremo do conjunto de distâncias. Pelo teorema de Glivenko–Cantelli, se a amostra vier da distribuição ${\displaystyle F(x)}$, então ${\displaystyle D_{n}}$ converge a 0 quase certamente no limite quando ${\displaystyle n}$ vai ao infinito. Kolmogorov fortaleceu este resultado ao oferecer efetivamente a razão desta convergência como mostrado abaixo. O Teorema de Donsker oferece um resultado ainda mais forte.

Na prática, a estatística exige um número relativamente grande de pontos de dados para que se rejeite adequadamente a hipótese nula.

A distribuição de Kolmogorov é a distribuição da variável aleatória

${\displaystyle K=\sup _{t\in [0,1]}|B(t)|}$

em que ${\displaystyle B(t)}$ é a ponte browniana. A função distribuição acumulada de ${\displaystyle K}$ é dada por^[4]

${\displaystyle \operatorname {Pr} (K\leq x)=1-2\sum _{k=1}^{\infty }(-1)^{k-1}e^{-2k^{2}x^{2}}={\frac {\sqrt {2\pi }}{x}}\sum _{k=1}^{\infty }e^{-(2k-1)^{2}\pi ^{2}/(8x^{2})},}$

que também pode ser expressa pela função teta de Jacobi ${\displaystyle \vartheta _{01}(z=0;\tau =2ix^{2}/\pi )}$. Tanto a forma da estatística do teste de Kolmogorov–Smirnov, como sua distribuição assintótica sob a hipótese nula foram publicadas por Kolmogorov,^[5] enquanto uma tabela da distribuição foi publicada por Smirnov.^[6] Relações de recorrência para a distribuição da estatística do teste em amostras finitas também foram divulgadas por Kolmogorov.^[5]

Sob a hipótese nula de que a amostra vem da distribuição hipotetizada ${\displaystyle F(x)}$,

${\displaystyle {\sqrt {n}}D_{n}{\xrightarrow {n\to \infty }}\sup _{t}|B(F(t))|}$

em distribuição, em que ${\displaystyle B(t)}$ é a ponte browniana.

Se ${\displaystyle F}$ for contínua, então, sob a hipótese nula, ${\displaystyle {\sqrt {n}}D_{n}}$ converge para a distribuição de Kolmogorov, que não depende de ${\displaystyle F}$. Este resultado também pode ser conhecido como teorema de Kolmogorov.

O teste de Kolmogorov–Smirnov para a qualidade do ajuste é construído pelo uso de valores críticos da distribuição de Kolmogorov.^[7] A hipótese nula é rejeitada no nível ${\displaystyle \alpha }$ se

${\displaystyle {\sqrt {n}}D_{n}>K_{\alpha },\,}$

em que ${\displaystyle K_{\alpha }}$ é encontrado a partir de

${\displaystyle \operatorname {Pr} (K\leq K_{\alpha })=1-\alpha .\,}$

A potência assintótica deste teste é 1.

Se a forma ou os parâmetros de ${\displaystyle F(x)}$ forem determinados a partir dos dados ${\displaystyle X_{i}}$, os valores críticos determinados desta forma são inválidos. Em tais casos, o método de Monte Carlo ou outros métodos podem ser exigidos e as tabelas foram preparadas para alguns casos. Os detalhes para as modificações exigidas para a estatística do teste e para os valores críticos para a distribuição normal e para a distribuição exponencial foram divulgados.^[8] Publicações mais recentes incluem a distribuição de Gumbel.^[9] O teste de Lillefors representa um caso especial desta questão para a distribuição normal. A transformação do logaritmo pode ajudar a superar casos em que os dados do teste de Kolmogorov parecem não se ajustar ao pressuposto de que veio da distribuição normal.

O teste de Kolmogorov–Smirnov deve ser adaptado para variáveis discretas.^[10] A forma da estatística do teste permanece igual à do caso contínuo, mas o cálculo de seu valor é mais sutil. Isto pode ser visto quando se computa a estatística do teste entre uma distribuição contínua ${\displaystyle f(x)}$ e uma função de etapa ${\displaystyle g(x)}$ que tem uma descontinuidade em ${\displaystyle x_{i}}$. Em outras palavras, o limite ${\displaystyle \lim _{x\rightarrow x_{i}}g(x)}$, se existir, é diferente de ${\displaystyle g(x_{i})}$. Assim, quando se computa a estatística

${\displaystyle \sup _{x}|g(x)-f(x)|=\max _{i}\left[\max \left(|g(x_{i})-f(x_{i})|,\lim _{x\rightarrow x_{i}}|g(x)-f(x_{i-1})|\right)\right],}$

não fica claro como realocar o limite, a não ser que se saiba o valor limitante da distribuição subjacente.

O teste Kolmogorov–Smirnov pode também ser usado para testar se duas distribuições de probabilidade unidimensionais subjacentes diferem entre si. Neste caso, a estatística de Kolmogorov–Smirnov é

${\displaystyle D_{n,m}=\sup _{x}|F_{1,n}(x)-F_{2,m}(x)|,}$

em que ${\displaystyle F_{1,n}}$ e ${\displaystyle F_{2,m}}$ são as funções distribuição empírica da primeira e da segunda amostra respectivamente e ${\displaystyle \sup }$ é a função supremo.

A hipótese nula é rejeitada ao nível ${\displaystyle \alpha }$ se

${\displaystyle D_{n,m}>c(\alpha ){\sqrt {\frac {n+m}{nm}}}.}$^[11]

${\displaystyle n}$ e ${\displaystyle m}$ são os tamanhos da primeira e da segunda amostras respectivamente. O valor de ${\displaystyle c({\alpha })}$ é dado na tabela abaixo para os níveis mais comuns de ${\displaystyle \alpha }$^[11]

${\displaystyle \alpha }$	0.10	0.05	0.025	0.01	0.005	0.001
${\displaystyle c({\alpha })}$	1.22	1.36	1.48	1.63	1.73	1.95

e, em geral, por

${\displaystyle c\left(\alpha \right)={\sqrt {-{\frac {1}{2}}\ln \left({\frac {\alpha }{2}}\right)}}.}$

O teste biamostral verifica se as duas amostras de dados vêm da mesma distribuição e não especifica qual é esta distribuição comum, isto é, se é normal ou não normal. Tabelas de valores críticos para este caso também foram publicadas.^[8][11] Estes valores críticos têm algo em comum com o teste de Anderson–Darling e o teste qui-quadrado, nomeadamente, o fato de que valores mais altos tendem a ser mais raros.^[12]

Enquanto o teste Kolmogorov–Smirnov é geralmente usado para testar se uma dada ${\displaystyle F(x)}$ é a distribuição de probabilidade subjacente de ${\displaystyle F_{n}(x)}$, o procedimento pode ser invertido para dar limites de confiança à própria ${\displaystyle F(x)}$. Caso se escolha um valor crítico da estatística de teste ${\displaystyle D_{\alpha }}$, tal que ${\displaystyle P(D_{n}>D_{\alpha })=\alpha }$, então a banda de largura ${\displaystyle \pm D_{\alpha }}$ em torno de ${\displaystyle F_{n}(x)}$ conterá inteiramente ${\displaystyle F(x)}$ com probabilidade ${\displaystyle 1-\alpha }$.

Um teste Kolmogorov–Smirnov de qualidade do ajuste multivariado e livre de distribuição foi proposto por Ana Justel, Daniel Peña e Rubén Zamar em 1997.^[13] O teste usa uma estatística construída pelo uso da transformação de Rosenblatt e um algoritmo é usado para a computação no caso bivariado. Um teste aproximado facilmente computado em qualquer dimensão também é apresentado.

A estatística do teste Kolmogorov–Smirnov precisa ser modificada se um teste semelhante for aplicado a dados multivariados. Ela não pode ser aplicada diretamente porque a diferença máxima entre duas funções distribuição acumulada conjuntas geralmente não é igual à diferença máxima de qualquer uma das funções distribuição complementares. Assim, a diferença máxima será diferente, dependendo se ${\displaystyle \Pr(x<X\land y<Y)}$ ou ${\displaystyle \Pr(X<x\land Y>y)}$ ou qualquer um dos dois outros arranjos possíveis for usado. Pode-se exigir que o resultado do teste usado não dependa da escolha feita.

Uma abordagem à generalização da estatística de Kolmogorov–Smirnov para dimensões mais elevadas que leva em conta a preocupação acima consiste em comparar as funções distribuição acumulada das duas amostras com todos os ordenamentos possíveis e tomar o maior conjunto das estatísticas K–S resultantes. Em ${\displaystyle d}$ dimensões, o número de ordenamentos é ${\displaystyle 2^{d}-1}$. Uma variação deste tipo foi proposta por J. A. Peacock^[14] e outra por G. Fasano e A. Francischini,^[15] ambas comparadas por R. H. C. Lopes.^[16] Valores críticos para a estatística do teste podem ser obtidos por simulações, mas isto depende da estrutura de dependência da distribuição conjunta.

• Teste de Kuiper

• Teste Kolmogorov–Smirnov na Encyclopedia of Mathematics (em inglês)
• Breve introdução do Departamento de Física do College of Saint Benedict e Saint John's University de Minnesota (em inglês)
• Breve introdução do Engineering Statistics Handbook (em inglês)
• Calculadora on-line com teste Kolmogorov–Smirnov (em inglês)

• Portal de probabilidade e estatística