Optymalna cena sprzedaży

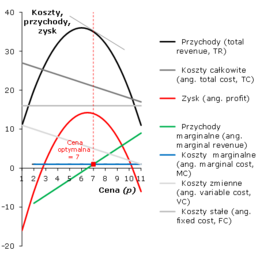
Optymalna cena sprzedaży – ustalony poziom sprzedaży produktu i jego ceny, przy której przedsiębiorstwo osiąga maksymalny zysk. Punkt zrównania przychodów krańcowych (ang. marginal revenue, MR) z kosztami krańcowymi (ang. marginal cost, MC).

${\displaystyle MR=MC}$

„Przedsiębiorstwo wytwarza jeden wyrób, ponosząc jednostkowe koszty zmienne w wysokości 300 zł i koszty stałe w wysokości 800 000 zł rocznie. Obecna cena zbytu wynosi 700 zł, a sprzedaż – 3000 sztuk. Kierownik działu sprzedaży oszacował, że każdy wzrost ceny sprzedaży o 100 zł spowoduje spadek sprzedaży o 1000 sztuk wyrobów i odwrotnie – każdy spadek o 100 zł spowoduje wzrost sprzedaży o 1000 wyrobów. Jaka jest optymalna cena zbytu dla tego wyrobu?”<ref>Ceny transferowe – teoria i praktyka, Sławomir Sojak, s. 52, PWN, Warszawa 2001.</ref>

Punkt 1. Kalkulacja kosztów stałych i zmiennych

• K = 300x + 800 000
• x – wielkość sprzedaży

Punkt 2. Kalkulacja maksymalnej ceny sprzedaży

• obecnie: cena 700 zł = 3000 sztuk
• wzrost ceny do 1000 zł = 0 sztuk
• maksymalna cena sprzedaży,
• c = 1000 – 0,1x
• c – cena
• x – wielkość sprzedaży

Punkt 3. Kalkulacja przychodów całkowitych ze sprzedaży

• c = 1000 – 0,1x / *x
• cx = 1000x – 0,1x²
• cx = P

Metoda ta polega na wyznaczeniu maksymalnego zysku dzięki wykreśleniu funkcji przychodów i kosztów.

Punkt 1. Wykonanie wykresu

• K = 300x + 800 000
• P = 1000x – 0,1x²

Wyznaczyliśmy dwa progi rentowności, gdzie K = P. Optymalny poziom sprzedaży jest w punkcie A. Temu punktowi odpowiada sprzedaż na poziomie 3500 sztuk.

Punkt 2. Kalkulacja optymalnego poziomu ceny

• c = 1000 – 0,1x
• x = 3500
• c = 1000 – 0,1 * 3500
• c = 650zł

Definicja rachunku kosztów krańcowych mówi, że maksymalny zysk ze sprzedaży dobra pojawia się przy takiej wielkości sprzedaży, kiedy następuje zrównanie ze sobą przychodów krańcowych (ang. marginal revenue – MR) i kosztów krańcowych (ang. marginal cost – MC) – (MR = MC).

Przychody i koszty krańcowe liczymy z pierwszej pochodnej funkcji przychodów i kosztów.

Punkt 1. Kalkulacja pochodnych funkcji

• P = 1000x – 0,1x²
• P’ = 1000 – 0,2x
• K= 300x + 800 000
• K’ = 300

Punkt 2. Zrównanie otrzymanych pochodnych

• 1000 – 0,2x = 300
• x = 3500

Punkt 3. Kalkulacja poziomu ceny sprzedaży

• c = 1000 – 0,1 * 3500
• c = 650 zł

• mechanizm kształtowania się cen

• „Ceny transferowe – teoria i praktyka” – S. Sojak, PWN, Warszawa 2001, s. 52-55
• „Rachunkowość zarządcza w warunkach inflacji” – S. Sojak, wydanie 3, TNOiK, Toruń 1999, s. 207-209
• „Kształtowanie cen. Strategie i procedury” – N. Hanna, M.R. Dodge, PWE, Warszawa 1997, s. 15