Բնական լոգարիթմ

Բնական լոգարիթմ, e հիմքով լոգարիթմ, որը իռացիոնալ հաստատուն է և հավասար է մոտ 2.72։ Այն նշանակվում է ${\displaystyle \ln x}$, ${\displaystyle \log _{e}x}$ կամ երբեմն ուղղակի ${\displaystyle \log x}$, երբ հիմքը ենթադրվում է ${\displaystyle e}$^[1]։ Սովորաբար լոգարիթմատակ արտահայտության ${\displaystyle x}$ արգումենտը իրական թիվ է, բայց այս հասկացությունը կարելի է ընդհանրացնել նաև կոմպլեքս թվերի համար։

Սահմանումից հետևում է, որ լոգարիթմական ֆունկցիան ${\displaystyle y=e^{x}}$ ցուցչային ֆունկցիայի հակադարձ ֆունկցիան է, ուստի նրանց գրաֆիկները համաչափ են առաջին և երրորդ քառորդների կիսորդի նկատմամբ։ Այն պատկանում է տրանսցենդենտ ֆունկցիաների դասին։

Բնական լոգարիթմները օգտակար են այն հանրահաշվական հավասարումների լուծման մեջ, որտեղ անհայտը ցուցիչում է։ Անփոխարինելի է մաթեմատիկական անալիզում, մաթեմատիկայի շատ բնագավառներում, կիրառական որոշ գիտություններում, ֆինանսական ոլորտի բազմաթիվ խնդիրներում (օրինակ բարդ տոկոսների հաշվման մեջ)։

x թվի բնական լոգարիթմ է կոչվում այն թիվը, որով պետք է աստիճան բարձրացնել e հիմքը՝ x ստանալու համար։ Այլ կերպ ասած․ բնական լոգարիթմը՝ ${\displaystyle \ln a}$ դա ${\displaystyle e^{x}=a}$ հավասարման ${\displaystyle x}$ լուծումն է։ Օրինակներ․

${\displaystyle \ln e=1}$, քանի որ ${\displaystyle e^{1}=e}$;

${\displaystyle \ln 1=0}$, քանի որ ${\displaystyle e^{0}=1}$։

${\displaystyle \ln a}$ բնական լոգարիթմը ${\displaystyle a}$ իրական թվի համար նույնպես սահմանվում է և ճիշտ է ցանկացած դրական ${\displaystyle a}$ թվի համար։

Բնական լոգարիթմը ցանկացած դրական իրական a թվի համար սահմանվում է նաև երկրաչափորեն՝ որպես ${\displaystyle y={\frac {1}{x}}}$ կորով սահմանափակված տիրույթի մակերես ${\displaystyle [1;a]}$ հատվածի վրա։

Լոգարիթմի սահմանումից էլ հենց ստացվում է հիմնական լոգարիթմական նույնությունը^[2]։

${\displaystyle e^{\ln a}=a}$

Կարևոր են նաև հետևյալ նույնությունները, որտեղ արժեքները համարվում են դրական․^[3]:

	Բանաձև	Օրինակ
Արտադրյալ	${\displaystyle \ln(xy)=\ln x+\ln y}$	${\displaystyle \ln(4\cdot 3)=\ln 4+\ln 3}$
Քանորդ	${\displaystyle \ln \left({\frac {x}{y}}\right)=\ln x-\ln y}$	${\displaystyle \ln \left({\frac {1}{e^{2}}}\right)=\ln(1)-\ln(e^{2})=0-2=-2}$
Աստիճան	${\displaystyle \ln(x^{p})=p\ln x}$	${\displaystyle \ln(64)=\ln(2^{6})=6\ln 2}$
Արմատ	${\displaystyle \ln {\sqrt[{p}]{x}}={\frac {\ln x}{p}}}$	${\displaystyle \ln {\sqrt {10}}={\frac {1}{2}}\ln 10}$

Այլ հատկություններ

• Արգումենտի աճի հետ աճում է նաև լոգարիթմը․ եթե ${\displaystyle 0<x<y,}$, ապա ${\displaystyle \ln x<\ln y}$;
• ${\displaystyle {\frac {h}{1+h}}\leqslant \ln(1+h)\leqslant h,}$, եթե ${\displaystyle h>-1}$։

Լոգարիթմը կարող է որոշված լինել ոչ միայն ${\displaystyle e}$ հիմքի, այլ ցանկացած դրական ${\displaystyle 1}$-ից տարբեր հիմքի համար։ ${\displaystyle a}$ հիմքով ${\displaystyle \log _{a}b}$ լոգարիթմը կարելի է ձևափոխել ^[4] բնական լոգարիթմի և հակառակը․

${\displaystyle \ln b={\frac {\log _{a}b}{\log _{a}e}}=\log _{a}b\cdot \ln a}$

${\displaystyle \log _{a}b={\frac {\ln b}{\ln a}}}$

Տասնորդական(${\displaystyle \lg x}$) լոգարիթմի և բնական լոգարիթմի կապը․ ^[5]

${\displaystyle \ln x\approx 2{,}30259\ \lg x;\quad \lg x\approx 0{,}43429\ \ln x}$

Երկուական (${\displaystyle \operatorname {lb} x}$) լոգարիթմի և բնական լոգարիթմի կապը․

${\displaystyle \ln x\approx 0,693147\operatorname {lb} x;\quad \operatorname {lb} x\approx 1{,}442695\ln x}$։

Եթե լոգարիթմվող թիվը ընդունենք որպես փոփոխական, ապա կստանանք ${\displaystyle y=\ln x}$ լոգարիթմական ֆունկցիան։ Այն որոշված է,երբ ${\displaystyle x>0}$։ Արժեքների տիրույթն է՝ ${\displaystyle E(y)=(-\infty ;+\infty )}$։ Այս կորը հաճախ անվանվում է լոգարիթմական^[6]։ Ֆունկցիան աճող է, անընդհատ ու դիֆերենցելի իրեն որոշման տիրույթում։ Աբցիսների առանցքը (${\displaystyle x=0}$) հանդիսանում է հորիզոնական ասիմպտոտ, քանի որ

${\displaystyle \lim _{x\to 0+0}\ln x=-\infty }$

Բնական լոգարիթմի ածանցյալը հավասար է․

${\displaystyle {\frac {d}{dx}}\ln x={\frac {1}{x}}}$։

Այս բանաձևի պարզության պատճառով է հենց լոգարիթմական ֆունկցիան կիրառվում մաթեմատիկական անալիզում և դիֆերենցիալ հավասարումներում։

Ինտեգրելով ածանցյալի բանաձևը ${\displaystyle x=1}$-ից մինչև ${\displaystyle x=b}$ միջակայքը, մենք կստանաք․

${\displaystyle \ln b=\int \limits _{1}^{b}{\frac {dx}{x}}}$

Այլ խոսքով․ բնական լոգարիթմը հավասար է ${\displaystyle y={\frac {1}{x}}}$ հիպերբոլով սահմանափակված մակերեսին x միջակայքի համար։

${\displaystyle y=1/x}$ ֆունկցիայի նախնականը ունի հետևյալ տեսքը․

${\displaystyle \int {dx \over x}=\ln |x|+C,}$

որտեղ ${\displaystyle C}$-ն ինտեգրման հաստատունն է։ Քանի որ ${\displaystyle y=1/x}$ ֆունկցիան կազմված է երկու ճյուղերից (մեկը դրական, մյուսը՝ բացասական ${\displaystyle x}$-երի համար), ապա ${\displaystyle y=1/x}$-ի նախնականների ընտանիքը նույնպես կազմված է երկու ենթաընտանիքներից, ընդ որում նրանց ինտեգրման հաստատունները անկախ են միմյանցից։ Բնական լոգարիթմից անորոշ ինտեգրալը հեշտ է գտնել մասերով ինտեգրմամբ։

${\displaystyle \int {\ln x\,\mathrm {d} x}=x\ln x-x+C}$

Մաթեմատիկական անալիզում և Դիֆերենցիալ հավասարումների տեսությունում մեծ դեր ունի ${\displaystyle f(x)}$ ֆունկցիայի լագարիթմական ածանցյալ հասկացությունը․

${\displaystyle {\frac {d}{dx}}\ln(f(x))={\frac {f'(x)}{f(x)}}}$։

Բնական լոգարիթմը վերլուծենք ըստ Թեյլորի շարքի․

${\displaystyle \ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+\dots }$

(շարք 1)

Այս շարքը, որը կոչվում է Մերկատորի շարք, զուգամիտում է, երբ ${\displaystyle -1<x\leqslant 1}$։ Մասնավորապես․

${\displaystyle \ln 2=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+\dots }$

Շարքը զուգամիտում է դանդաղ։ Նրանից կարելի է ստանալ առավել հարմար բանաձև․

${\displaystyle \ln \left({\frac {1+x}{1-x}}\right)=2\left(x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\dots \right)}$

(շարք 2)

Այս շարքը արդեն արագ է զուգամիտում։ Բացի այդ, բանաձևի ձախ մասով կարելի է արտահայտել ցանկացած դրական թվի լոգարիթմ։ Այս ալգորիթմով հնարավոր է հաշվել լոգարիթմների արժեքները, բայց այն դժվար է։ Շատ թվանշանների առկայության դեպքում Թեյլորի շարքով հաշվարկը էֆեկտիվ չէ։ Կիրառելի է որպես այլընտրանքային միջոց Նյուտոնի մեթոդը։ Դիտարկվում է հետևյալ բանաձևը․ ^[7][8]։

${\displaystyle \ln x\approx {\frac {\pi }{2M(1,4/s)}}-m\ln 2}$

որտեղ ${\displaystyle M}$ դա 1 և 4/s-ի թվաբանա-երկրաչափական միջինն է։

${\displaystyle s=x\,2^{m}>2^{p/2}}$։

Բերենք մի քանի օգտակար սահմանների օրինակներ լոգարիթմների համար ^[9]․

${\displaystyle \lim _{x\to 0}{\frac {\ln(1+x)}{x}}=1}$

${\displaystyle \lim _{x\to 0^{+}}x^{b}\ln x=0\quad (b>0)}$

${\displaystyle \lim _{x\to \infty }{\frac {\ln x}{x^{b}}}=0\quad (b>0)}$

${\displaystyle \ln x=\lim _{n\to \infty }n\left({\sqrt[{n}]{x}}-1\right)=\lim _{n\to \infty }n\left(1-{\frac {1}{\sqrt[{n}]{x}}}\right)}$

${\displaystyle \ln x=\lim _{h\to 0}{\frac {x^{h}-1}{h}}}$

Լոգարիթմի ներկայացման համար կիրառվում են մի քանի անընդհատ կոտորակներ․

${\displaystyle \ln(1+x)={\frac {x^{1}}{1}}-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+{\frac {x^{5}}{5}}-\dots ={\cfrac {x}{1-0x+{\cfrac {1^{2}x}{2-1x+{\cfrac {2^{2}x}{3-2x+{\cfrac {3^{2}x}{4-3x+{\cfrac {4^{2}x}{5-4x+\ddots }}}}}}}}}}}$

${\displaystyle \ln \left(1+{\frac {2x}{y}}\right)={\cfrac {2x}{y+{\cfrac {x}{1+{\cfrac {x}{3y+{\cfrac {2x}{1+{\cfrac {2x}{5y+{\cfrac {3x}{1+\ddots }}}}}}}}}}}}={\cfrac {2x}{y+x-{\cfrac {(1x)^{2}}{3(y+x)-{\cfrac {(2x)^{2}}{5(y+x)-{\cfrac {(3x)^{2}}{7(y+x)-\ddots }}}}}}}}}$

Բնական լոգարիթմի մասին առաջին տեղեկությունները հայտնվեցին 1619 թվականին, երբ լոնդոնցի մաթեմատիկայի ուսուցիչ Ջոն Սպենդելը վերահրատարակեց Նեպերի լոգարիթմական աղյուսակը՝ լրացնելով այն բնական լոգարիթմի աղյուսակներով^[10]։ 1649 թվականին բելգիացի մաթեմատիկոս Գրեգուար դը Սեն-Վենսանը ցույց տվեց, որ ${\displaystyle y={\frac {1}{x}}}$ հիպերբոլով սահմանափակված պատկերի մակերեսը փոխվում է լոգարիթմական օրենքով, և առաջարկեց դրանց անվանել «հիպերբոլական» լոգարիթմներ^[11]։ «Բնական լոգարիթմ» տերմինը առաջին անգամ օգտագործել է Նիկոլաս Մերկատորը իր «Logarithmotechnia» աշխատությ��ւնում, որը հրապարակվեց 1668 թվականին^[12]։ Այստեղ Մերկատորը ներկայացրեց լոգարիթմի վերլուծությունը Մերկատորի շարքով։ XVII—XVIII դարերում Գոթֆրիդ Լայբնիցը և Իոհան Բեռնուլլին բնական լոգարիթմը փորձեցին տարածել կոմպլեքս թվերի վրա, բայց ստեղծել ամբողջական տեսություն նրանց չհաջողվեց։ Բացասական և կոմպլեքս թվերի լոգարիթմների տեսությունը հրապարակվեց 1747-1751 թվականներին Էյլերի կողմից, և չի տարբերվում ժամանակակից տեսությունից^[13]։

Կոմպլեքս լոգարիթմը անալիտիկ ֆունկցիա է, որը ստացվում է իրական լոգարիթմը կոմպլեքս հարթության վրա տարածելով (բացի 0-ից)։ Կոմպլեքս լոգարիթմի ֆունկցիան բազմարժեք է։ Սահմանում Կոմպլեքս ${\displaystyle z}$ թվի ${\displaystyle \mathrm {Ln} \,z}$ բնական լոգարիթմը դա ${\displaystyle e^{w}=z.}$ հավասարման լուծումն է ${\displaystyle w}$^[6]։

${\displaystyle z}$ ոչ զրոյական թիվը կարելի է ներկայացնել ${\displaystyle z=r\cdot e^{i(\varphi +2\pi k)}\;\;,}$ բանաձևով, որտեղ ${\displaystyle k}$ —կամայակն ամբողջ թիվ է Ապա ${\displaystyle \mathrm {Ln} \,z}$ որոշվում է

${\displaystyle \mathrm {Ln} \,z=\ln r+i\left(\varphi +2\pi k\right)}$ բանաձևով։ Այստեղ ${\displaystyle \ln \,r=\ln \,|z|}$ իրական լոգարիթմն է^[14]։ Այսպիսով․

${\displaystyle \mathrm {Ln} \,z}$ կոմպլեքս լոգարիթմը գոյություն ունի ցանկացած ${\displaystyle z\neq 0}$ համար, և նրա իրական մասը որոշվում է միանշանակորեն, իսկ կեղծ մասը ունի անվերջ բազմությամբ լուծումներ՝ տարբերվելով միմյանցից ${\displaystyle 2\pi }$ արժեքով։

Բացասական թվի լոգարիթմը որոշվում է^[14]։

${\displaystyle \mathrm {Ln} (-x)=\ln x+i\pi (2k+1)\qquad (x>0,\ k=0,\pm 1,\pm 2\dots )}$ բանաձևով

Օրինակներ

${\displaystyle \ln(1)=0;\;\mathrm {Ln} (1)=2k\pi i}$

${\displaystyle \ln(-1)=i\pi ;\;\mathrm {Ln} (-1)=(2k+1)i\pi }$

${\displaystyle \ln(i)=i{\frac {\pi }{2}};\;\mathrm {Ln} (i)=i{\frac {4k+1}{2}}\pi }$

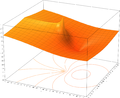
• Բնական լոգարիթմի ֆունկցիաները կոմպլեքս հարթության վրա(գլխավոր ճյուղ)
• 
  ${\displaystyle z=Re(\ln(x+iy))|}$
• 
  ${\displaystyle z=Im(\ln(x+iy))|}$
• 
  ${\displaystyle z=|\ln(x+iy)|}$
• 
  Երեք նախկին գրաֆիկների ընդհանրությունը

• Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
  • Переиздание: АСТ, 2003, ISBN 5-17-009554-6.
• Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
• Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с.
• Ա․Գ․Սվեշնիկով, Ա․Ն․Տիխոնով; Կոմպլեքս փոփոխականի ֆունկցիաների տեսություն, Մ․, Նաուկա,1966,էջ304։
• Գ․Մ․Ֆիխտենգոլց; Դիֆերենցիալ և ինտեգրալ հաշիվ,6-րդ հրատ․, — Մ.: Նաուկա, 1966. — էջ 680։