גל מישורי

גל מישורי הוא גל בעל חזית גל בצורת מישור. גל מישורי הוא אופן התפשטות אפשרי של גל בחלל הפתוח ובמובילי גל שונים. גל בעל חזית גל בצורת מישור אינסופי אינו פיזיקלי, אך גלים שונים הם בקירוב גלים מישוריים. לדוגמה, גל כדורי הוא בקירוב גל מישורי הרחק מהמקור, וכך אור השמש המגיע לכדור הארץ הוא בקירוב גל מישורי.

גל הוא פונקציה של הזמן והמרחב המקיימת את משוואת הגלים: ${\displaystyle \ {\frac {\partial ^{2}}{\partial t^{2}}}y({\vec {r}},t)=v^{2}\ \nabla ^{2}y({\vec {r}},t)}$.

פונקציה שפותרת את משוואת הגלים היא פונקציה של המרחב שמשתנה בזמן כך שהיא שומרת על צורתה אך ערכיה נשמרים בנקודות במרחב שנעות במהירות קבועה ששווה ל-${\displaystyle \,v}$. הפתרון היסודי של המשוואה במערכת צירים קרטזית הוא:

${\displaystyle y({\vec {r}},t)=Ae^{i({\vec {k}}\cdot {\vec {r}}-\omega t)}\,}$

כאשר A קבוע, i היחידה המדומה, ${\displaystyle {\vec {r}}}$ הוא וקטור ההעתק, ${\displaystyle \omega }$ התדירות הזוויתית של הפתרון ו-${\displaystyle {\vec {k}}}$ הוא וקטור כלשהו, הנקרא וקטור הגל, המקיים:

${\displaystyle \omega =v|{\vec {k}}|}$

בכל רגע נתון, חזית הגל - המשטח שווה המופע שעל פניו ${\displaystyle \ y({\vec {r}})}$ קבוע, הוא המקום הגאומטרי המקיים:

${\displaystyle {\vec {r}}\cdot {\vec {k}}=const}$

וזוהי משוואה המתארת מישור המאונך לווקטור ${\displaystyle {\vec {k}}}$. המישורים שווי המופע נעים בזמן במהירות קבועה v ובכיוון קבוע, ככיוון וקטור הגל ${\displaystyle {\vec {k}}}$.

מאחר שמשוואת הגלים היא הומוגנית, גם צירוף ליניארי של פתרונות בעלי תדירויות זוויתיות שונות ומשרעת שתלויה בתדירות הזוויתית הוא פתרון. לכן, בעזרת פתרון יסודי זה ניתן לפרוש פונקציה מחזורית כללית כטור פורייה ופונקציה כללית שאינה בהכרח מחזורית כהתמרת פורייה.

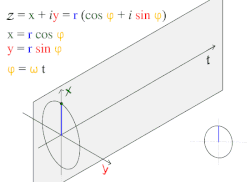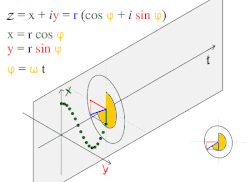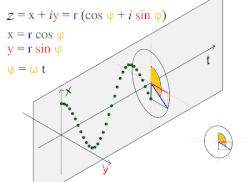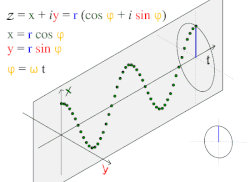
הגל המישורי הפשוט והנפוץ ביותר הוא גל סינוסי המתואר על ידי המשוואה:

${\displaystyle y(x,t)=A\sin(kx-\omega t)\,}$.

גל זה מתקדם בכיוון x וערכו אינו תלוי בקואורדינטות y,z. ניתן לכתוב אותו כסכום של הפתרון היסודי והצמוד המרוכב שלו לפי נוסחת אוילר, או כלקיחת החלק הממשי (או המדומה) שלו. אם מייצגים את ערך גל האקספוננט המרוכב הקבוע על פני מישור שווה מופע במישור המרוכב כתלות בזמן, אז ההיטלים שלו על הציר הממשי ועל הציר המדומה הם גלים סינוסיים בעלי הפרש מופע של ${\displaystyle {\frac {\pi }{2}}}$.

דוגמאות לגלים מישוריים סינוסיים הן השדה החשמלי בין לוחות קבל בזרם חילופין והשדה האלקטרומגנטי של מקור אור מונוכרומטי נקודתי הרחק מהמקור.

במכניקת הקוונטים גלים מישוריים מהווים פתרון למשוואת שרדינגר עבור חלקיק חופשי. פתרון מהצורה של גל מישורי מתאר חלקיק בעל תנע קווי קבוע וידוע מראש. פתרון זה למשוואת שרדינגר יהיה פתרון מהצורה:

${\displaystyle \psi (x,t)=e^{\frac {i({\vec {p}}\cdot {\vec {r}}-Et)}{\hbar }}}$

כאשר מתקיים הקשר הקלאסי ${\displaystyle E={\frac {p^{2}}{2m}}}$.

ייצוג חלקיק כגל הוצע בהשערת דה ברויי אשר הניחה שכפי שישנה דואליות גל-חלקיק עבור אור, כך תהייה דואליות שכזו לחלקיקים אחרים (ובפרט לאלקטרונים). ייצוג חלקיק חופשי כגל משורי מהווה הצדקה עבור משוואת שרדינגר וניתן באמצעותו לנסח תופעות טבע מרובות כגון חוק סנל וחוקי פרנל.

מדיה וקבצים בנושא גל מישורי בוויקישיתוף

גלים
מאפיינים	משרעת • תדירות • מופע • אורך גל • וקטור גל • מספר גל • מהירות פאזה • מהירות חבורה • קיטוב
תופעות	החזרה • העברה • שבירה • התאבכות • עקיפה • נפיצה • בליעה
מושגים	גל עומד • אפנון • חבילת גלים • תווך • מתנד הרמוני • תהודה • אפקט דופלר
אנליזה	משוואת הגלים • משוואת הלמהולץ • עקרון הויגנס • עקרון פרמה • חוקי פרנל
סוגי גלים	גל מישורי • גל כדורי • גל רוחב • גל אורך • פולס • קרינה אלקטרומגנטית • גל קול • גל (מים) • פונקציית גל